КОНТРОЛЬНЫЕ ЗАДАНИЯ

⇐ Предыдущая 21 22 23 24 25 26 272829 30 Следующая ⇒

Контрольная работа №1

ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ. КОМПЛЕКСНЫЕ ЧИСЛА

1–10. Данные системы решить методом Гаусса:

1. а) ;	б) ;
в) .
2. а) ;	б) ;
в) .
3. а) ;	б) ;
в) .
4. а) ;	б) ;
в) .
5. а) ;	б) ;
в) .
6. а) ;	б) ;
в) .
7. а) ;	б) ;
в) .
8. а) ;	б) ;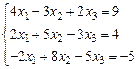
в) .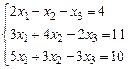
9. а) ;	б) ;
в) .
10. а) ;	б) ;
в) .

Вычислить определитель, используя теорему Лапласа.

11. ;	12. ;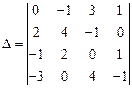
13. ;	14. ;
15. ;	16. ;
17. ;	18. ;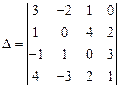
19. ;	20. .

Решить систему, используя правило Крамера.

21. ;	22. ;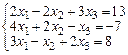
23. ;	24. ;
25. ;	26. ;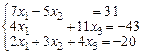
27. ;	28. ;
29. ;	30. .

31–40. Даны матрицы А, B, C, D. Найти произведения матриц: А × С,
A × С × D, B × D, A × B:

31. ; ; ;

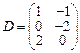
32. ; ; ;

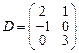
33. ; ; ;

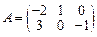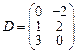
34. ; ; ;

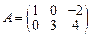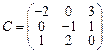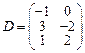
35. ; ; ;

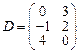
36. ; ; ;

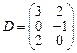
37. ; ; ;

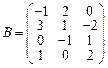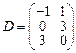
38. ; ; ;

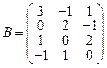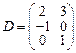
39. ; ; ;

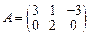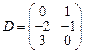
40. ; ; ;

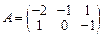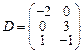
Решить систему средствами матричного исчисления. Сделать проверку для обратной матрицы.

41. ;	42. ;
43. ;	44. ;
45. ;	46. ;
47. ;	48. ;
49. ;	50. .

Даны два комплексных числа и. Найти: 1); 2); 3); 4).

Указать действительную и мнимую части комплексных чисел.

51. z ₁ = 3 – 2 i, z ₂ = 5 + 4 i;	52. z ₁ = –4 + i, z ₂ = 6 + 2 i;
53. z ₁ = 7 – i, z ₂ = –3 – 4 i;	54. z ₁ = 8 + 2 i, z ₂ = –6 – i;
55. z ₁ = –9 – 4 i, z ₂ = 2 – 5 i;	56. z ₁ = 1 – 8 i, z ₂ = –3 – 2 i;
57. z ₁ = 4 + 5 i, z ₂ = –6 – 7 i;	58. z ₁ = –3 + 9 i, z ₂ = 4 + i;
59. z ₁ = –2 – 2 i, z ₂ = 5 – 3 i;	60. z ₁ = 9 + i, z ₂ = –7 – 8 i.

61–70. Найти корни уравнений:

61. z ² + 3 z + 5 = 0;	62. z ² – 4 z + 6 = 0;
63. z ² – 5 z + 7 = 0;	64. z ² + 2 z + 9 = 0;
65. z ² – 3 z + 4 = 0;	66. z ² + 4 z + 5 = 0;
67. z ² – 2 z + 6 = 0;	68. z ² + 5 z + 8 = 0;
69. z ² – 6 z + 12 = 0;	70. z ² + 6 z + 9 = 0;

Контрольная работа №2

ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

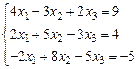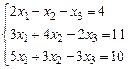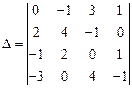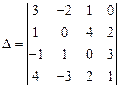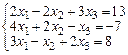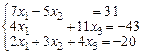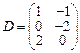
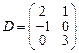
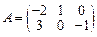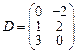
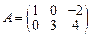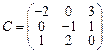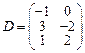
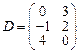
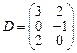
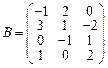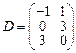
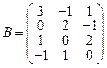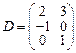
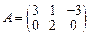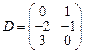
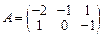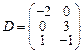
⇐ Предыдущая 21 22 23 24 25 26 272829 30 Следующая ⇒

Дата добавления: 2014-11-10; просмотров: 634. Нарушение авторских прав; Мы поможем в написании вашей работы!

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...

Теория усилителей. Схема Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах...

Трамадол (Маброн, Плазадол, Трамал, Трамалин) Групповая принадлежность · Наркотический анальгетик со смешанным механизмом действия, агонист опиоидных рецепторов...

Мелоксикам (Мовалис) Групповая принадлежность · Нестероидное противовоспалительное средство, преимущественно селективный обратимый ингибитор циклооксигеназы (ЦОГ-2)...

Менадиона натрия бисульфит (Викасол) Групповая принадлежность •Синтетический аналог витамина K, жирорастворимый, коагулянт...

Опухоли яичников в детском и подростковом возрасте Опухоли яичников занимают первое место в структуре опухолей половой системы у девочек и встречаются в возрасте 10 – 16 лет и в период полового созревания...

Способы тактических действий при проведении специальных операций Специальные операции проводятся с применением следующих основных тактических способов действий: охрана...

Искусство подбора персонала. Как оценить человека за час Искусство подбора персонала. Как оценить человека за час...

Studopedia.info - Студопедия - 2014-2024 год . (0.009 сек.) русская версия | украинская версия