Решение. 1) Областью определения функции является вся числовая прямая
1) Областью определения функции является вся числовая прямая. 2) Найдем 3) Решим уравнение 4)
Определим знак производной  слева и справа от точек слева и справа от точек  , ,  . .
В интервале
3.8.9. Асимптоты Асимптотой кривой называется такая прямая, к которой неограниченно приближается точка кривой при неограниченном удалении ее от начала координат. Различают три вида асимптот: горизонтальные, вертикальные и наклонные. Кривая Кривая Для определения наклонной асимптоты
Наклонные асимптоты кривой Если k = 0, а b имеет конечное значение, то асимптота будет горизонтальной, у = b. Пример 5. Найти асимптоты кривой Решение. При х = 3 данная кривая имеет бесконечный разрыв. Поэтому прямая х = 3 есть ее вертикальная асимптота.
Выясним, имеет ли график функции наклонные асимптоты:
Подставляя найденные значения k и
3.8.10. Общая схема исследования функций и построение их графиков Общее исследование функций и построение их графиков удобно выполнять по следующей схеме: 1. Найти область определения функции. 2. Найти точки разрыва функции и ее односторонние пределы в этих точках. 3. Выяснить вопрос о четности и нечетности функции. 4. Найти точки пересечения графика функции с осями координат. 5. Найти асимптоты графика функции. 6. Найти интервалы возрастания и убывания функции и точки экстремума. 7. Найти интервалы выпуклости и вогнутости графика функции, точки перегиба. 8. Построить график функции, используя все полученные результаты исследования. Если их окажется недостаточно, то следует найти еще несколько точек графика функции исходя из ее уравнения. Построение графика функции целесообразно выполнять по его элементам, вслед за выполнением отдельных пунктов исследования. Пример 6. Исследовать функцию
|

 ;
;  .
.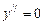 :
:  .
.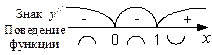
 кривая выпукла вверх, а в интервале
кривая выпукла вверх, а в интервале 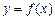 имеет горизонтальную асимптоту
имеет горизонтальную асимптоту 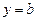 только в том случае, когда существует конечный предел функции
только в том случае, когда существует конечный предел функции  при х ® ¥ или при х ® –¥, т.е. если
при х ® ¥ или при х ® –¥, т.е. если  или
или  .
.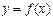 имеет вертикальную асимптоту
имеет вертикальную асимптоту  , если при х ® а, х ® а – 0 или при х ® а + 0,
, если при х ® а, х ® а – 0 или при х ® а + 0, 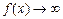 . Для определения вертикальных асимптот надо отыскать те значения аргумента, вблизи которых
. Для определения вертикальных асимптот надо отыскать те значения аргумента, вблизи которых  неограниченно возрастает по абсолютной величине.
неограниченно возрастает по абсолютной величине. кривой
кривой 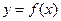 надо найти числа k и b из формул:
надо найти числа k и b из формул: ,
,  .
.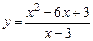 .
.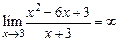 .
. ;
;
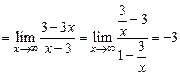 .
. в уравнение y = kx + b, получим уравнение наклонной асимптоты
в уравнение y = kx + b, получим уравнение наклонной асимптоты  .
. и построить ее график.
и построить ее график.


