Решение. 1) Областью существования функции является весь бесконечный интервал (–¥, ¥)
1) Областью существования функции является весь бесконечный интервал (–¥, ¥). 2) Находим 3) Решаем уравнение х (х 2 – 2 х – 3) = 0 Þ х 1 = 0, х 2 = 3, х 3 = –1. 4) Располагаем критические точки в порядке возрастания абсцисс: –1; 0; 3. 5) Рассмотрим интервалы Выберем внутри каждого из этих интервалов произвольную точку и определим в этой точке знак первой производной. В интервале
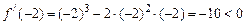 . В интервале (–1, 0) возьмем точку . В интервале (–1, 0) возьмем точку  , ,  ; в интервале (0, 3) возьмем точку ; в интервале (0, 3) возьмем точку х = 1, 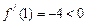 ; в интервале (3, ¥) возьмем точку х = 4, ; в интервале (3, ¥) возьмем точку х = 4,  . Точку в интервале можно брать любую. . Точку в интервале можно брать любую.
В критической точке х = –1 имеет место минимум, в точке Найдем экстремальные значения функции:
Определим наименьшее и наибольшее значение функции на отрезке [–2, 4]. Этот отрезок содержит внутри себя все критические точки. Так как значения функции в критических точках уже вычислены, остается вычислить значения функции на концах отрезка:
Сравнивая все вычисления, видим, что наибольшего значения функция достигает на левом конце отрезка при х = –2, а наименьшего – в критической точке х = 3.
3.8.7. Направление выпуклости кривой. Точки перегиба Если в некотором интервале кривая расположена ниже любой своей касательной, то она называется выпуклой вверх, а если она расположена выше любой своей касательной, то называется выпуклой вниз в этом интервале.
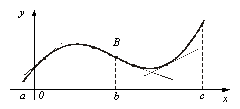
Точкой перегиба называется точка на кривой, где меняется направление ее выпуклости. Рис. 23
На рис.23 в интервале (а, b) кривая выпукла вверх, в интервале (b, с) она выпукла вниз, а точка B есть точка перегиба. Направление выпуклости кривой Абсциссы точек перегиба кривой 1) найдем 2) определим знак Пример 4. Определить направление выпуклости и точки перегиба кривой
|

 :
: 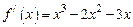 .
. т.е.
т.е. 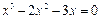 ;
; .
.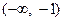 возьмем, например, точку х = –2;
возьмем, например, точку х = –2;
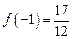 ,
,  ,
,  .
. ;
; 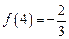 .
.
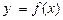 характеризуется знаком второй производной
характеризуется знаком второй производной  : если в некотором интервале
: если в некотором интервале  , то кривая выпукла вниз, а если
, то кривая выпукла вниз, а если  , то кривая выпукла вверх в этом интервале.
, то кривая выпукла вверх в этом интервале.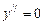 или не существует;
или не существует;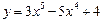 .
.


