Найти производные данных функций
131–140. Найти уравнение касательной и нормали к кривой
141–150. Найти наибольшее и наименьшее значения функции
151–160. Исследовать методами дифференциального исчисления функцию и построить её график.
ЛИТЕРАТУРА
1. Жолков С.Ю. Математика и информатика для гуманитариев. М.: Гордарики, 2002. 2. Кабарухина В.А. Методические указания по математике для студентов первого курса. Часть I. Таганрог, 2000. 3. Кабарухина В.А. Методические указания по математике для студентов первого курса. Часть II. Таганрог, 2001. 4. Кабарухина В.А. Методические указания по математике для студентов первого курса. Часть III. Таганрог, 2001. 5. Кабарухина В.А., Лепская И.А., Лященко Т.В. Методические указания по математике для студентов первого курса. Часть IV. Таганрог, 2003. 6. Кабарухина В.А., Лепская И.А., Лященко Т.В. Методические указания по математике для студентов первого курса. Часть V. Таганрог, 2003 7. Красс М.С. Математика для экономических специальностей. М.: Дело, 2002. 8. Красс М.С. Основы математики и ее приложения в экономическом образовании. М.: Дело, 2002. 9. Кремер Н.Ш. Высшая математика для экономистов. М.: ЮНИТИ, 1998. 10. Солодовников А.С. Математика в экономике. М.: Финансы и статистика. 1999. Ч. 1, 2. 11. Шипачев В.С. Курс высшей математики. М.: ПРОСПЕКТ, 2002.
СОДЕРЖАНИЕ ПРЕДИСЛОВИЕ.. 3
|


 ;
;
 ;
;
 ;
;
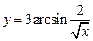 .
.
 ;
;

 ;
;
 ;
;
 .
.
 ;
;

 ;
;
 ;
;

 ;
;

 ;
;
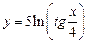 ;
;
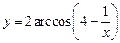 .
.
 ;
;
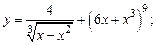
 ;
;
 ;
;
 .
.
 ;
;
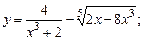
 ;
;
 ;
;
 .
.
 ;
;
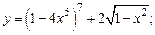
 ;
;
 ;
;
 .
.
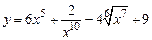 ;
;

 ;
;
 .
.
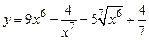 ;
;

 ;
;
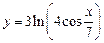 ;
;
 .
.
 ;
;

 ;
;
 ;
;
 .
.
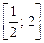
 , [–1; 4]
, [–1; 4]
 ; [–2; 1]
; [–2; 1]
 ;
;
 ;
;



