Решение. 1. Областью определения данной функции, как и всякого многочлена, является вся числовая ось
1. Областью определения данной функции, как и всякого многочлена, является вся числовая ось. 2. Функция не имеет точек разрыва. 3. Функция не является ни четной, ни нечетной, т.к.
4. Найдем точки пересечения графика функции с осями координат. При x = 0 из данного уравнения найдем y = 0, т.е. точка (0, 0). При y = 0 найдем x = 0 и x = 4, т.е. точки (0, 0) и (4, 0). 5. Вертикальных асимптот график функции не имеет, так как она всюду непрерывна. Выясним, имеет ли график функции наклонные асимптоты:
Следовательно, наклонных асимптот нет. 6. Найдем точки экстремума функции. Первая производная функции равна:
Найдем критические точки
Следовательно, х = 3, точка максимума В интервале (–¥, 0) функция возрастает, а в интервале 7. Найдем интервалы выпуклости и вогнутости и точки перегиба:
Таблица 1
Следовательно, график имеет две точки перегиба (0, 0) и (2; 3, 2). В интервале (–¥, 0) и (2, ¥) график обращен выпуклостью вверх, а в интервале (0, 2) – выпуклостью вниз. Используя полученные результаты, построим график данной функции. Удобно взять дополнительную точку: х = –2, у = –9, 6, т.е. точка (–2; –9, 6) (рис. 24). Рис. 24
|
, 
, 
.
.
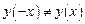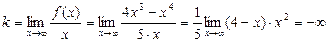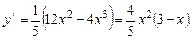
в точках х = 0 и х = 3, т.е. функция имеет две критические точки. Разобьем область определения функции критическими точками на интервалы, определим знак производной в каждом интервале и поведение функции. Для удобства построим следующую таблицу.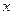
.
.
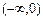
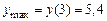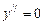при х = 0 и х = 2, т.е., х = 0 и х = 2 могут быть абсциссами точек перегиба. Для их исследования удобно построить таблицу:
