Тема№5 Прогнозирование на базе одиночных временных рядов
Разработка прогнозов на базе одиночных временных рядов выполняется по отдельным этапам. На первом этапе выявляется форма зависимости социально–экономического показателя от фактора времени Первый метод более универсальный, а поэтому имеет более широкую область применения. Второй применяется в тех случаях, когда исследователь считает, что для данного ряда в качестве прогнозирующей функции можно использовать полином При реализации графического метода не всегда по исходным данным можно определить характер зависимости признака от фактора времени В этих ситуациях исходные данные подвергаются дополнительной статистической обработке путем расчета скользящих средних. В зависимости от количества элементов, включаемых в период сглаживания, различают скользящие средние с четным и нечетным интервалами времени. При расчете скользящих средних с нечетным количеством элементов искомые величины на первом этапе, имеют " адресную привязку"; при нечетном – искомые величины определяются через посредство " плавающих скользящих средних". В зависимости от характера периодов сглаживания применяют следующие формулы: трехчленная
пятичленная
четырехчленная
Из полученных скользящих средних формируется новый временной (динамический) ряд, в котором в большей степени усилено влияние на формирование социально–экономического показателя закономерно действующих во времени факторов. Благодаря этому при графическом анализе более четко просматривается форма изменения анализируемого признака во времени. В основу использования метода конечных разностей положено свойство полинома Конечные разности
…………
Предположим, что конечные разности 3–го порядка преимущественно стремятся к нулю
Следовательно, в данном примере тенденция социально–экономического признака во времени описывается полиномом 2–й степени:
Графический способ и метод конечных разностей позволяют получить предварительную оценку о форме связи социально – экономического признака с фактором времени Изменения социально–экономических признаков во времени могут быть самыми разнообразными: равномерными, ускоренными, с резкими переходами, с пределами насыщения и другими тенденциями. Это свидетельство того, что научно обоснованный прогноз требует проведения глубокого не только количественного, но и качественного анализа в целях выявления действующих внутренних и внешних причин на характер поведения во времени исследуемого социально–экономического признака. Выявленная зависимость прогнозируемого признака от фактора времени Для представления тренда в виде конкретного выражения необходимо рассчитать его параметры, используя при этом различные математические способы. Наибольшее распространение, вероятно по своей простоте, для расчета параметров, получил метод наименьших квадратов. Суть этого метода заключается в построении и решении системы нормальных уравнений. Построение системы нормальных, уравнений требует соблюдения определенного правила, суть которого, рассмотрим на примере прогнозирующей функции вида: Правило построения системы нормальных уравнений: 1.Записывается общий вид прогнозирующей функции – 2.Выявляются искомые параметры – 3.Анализируются искомые параметры на предмет наличия (отсутствия) свободного элемента – 3.1. При наличии такого элемента первое нормальное уравнение строится следующим образом: свободный элемент
3.2. При отсутствии свободного элемента этап 3.1 не отрабатывается; 4. Последующие нормальные уравнения конструируются путем поочередного умножения элементов прогнозирующей модели на сомножители очередных искомых параметров. Полученные произведения суммируются в рамках области исследования. 4.1. По параметру
4.2. По параметру
Количество нормальных уравнений в системе соответствует числу искомых параметров:
В тех случаях, когда прогнозирующая функция представлена трендом, отличным от полинома После нахождения в конкретной форме прогнозирующей функции приступают к оценке правильности выбранной ee формы, то есть насколько прогнозирующая функция в данной форме точно аппроксимирует (описывает) положение исходных точек на координатном поле. Такая оценка выполняется, с помощью критерия Фишера Расчетные значения критерия Фишера
где дисперсии. Перечисленные дисперсии определяются по соответствующим формулам:
где
Под степенью свободы необходимо понимать возможное количество функционально несвязанных между собой вариантов колеблемости некоторого признака. Оценка правильности выбора прогнозирующих функций по форме выполняется на основе сравнения Табличное значение критерия Фишера определяется по специальным таблицам на пересечении линий, проведанных через степени свободы В зависимости от формул расчета критерия Фишера определение степеней свободы имеет некоторые особенности: для формулы (5.10)
для формулы (5.11)
При сравнении расчетных значений, с табличными
При использовании нескольких конкурирующих функций предпочтение отдается той функции, у которой После оценки функции по С помощью этой проверки оценивается тождественность тенденций, сложившихся в выборочных наблюдениях, в рамках области исследования, и в представительной выборке. Для линейных уравнений тренда – 1) определяют случайные ошибки по формулам:
где
2) рассчитывают
Полученные расчетные Если Если Для построения доверительной зоны линий регрессии для каждой временной точки области исследования определяют ординаты на верхней и нижней граничных кривых. Значения указанных ординат определяют по формулам.
где доверительной зоны;
времени
Полученные точки на соответствующих граничных кривых соединяют линиями, получая при этом графическое изображение доверительной зоны для линии регрессии. В целом на точность прогноза оказывают влияние не только статистическая значимость параметров уравнений регрессии, но и отклонения между расчетными и фактическими значениями признака. Доверительные интервалы для индивидуальных значений признака рассчитывают по формуле:
Индивидуальные прогнозные значения признака с учетом влияния всех возмущающих факторов можно определить по формуле:
Зная
|

 . Для нахождения этой формы можно применять различные методы. Наиболее распространенными в практике прогнозирования, являются графический метод и метод конечных разностей.
. Для нахождения этой формы можно применять различные методы. Наиболее распространенными в практике прогнозирования, являются графический метод и метод конечных разностей. степени.
степени. при
при  (5.1)
(5.1)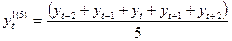 при
при  (5.2)
(5.2) при
при  – го порядка
– го порядка  .
.

 , (5.4)
, (5.4) . Для нахождения степени полинома необходимо решить следующее простейшее уравнение:
. Для нахождения степени полинома необходимо решить следующее простейшее уравнение:

 , (5.5)
, (5.5) . На данном этапе прогнозирования необходимо тщательно изучить характер изменения анализируемого признака, исходя из его природы, используя при этом логические, математические и экономические методы анализа.
. На данном этапе прогнозирования необходимо тщательно изучить характер изменения анализируемого признака, исходя из его природы, используя при этом логические, математические и экономические методы анализа.
 ;
; ;
; умножают на число точек, входящих в состав динамического ряда –
умножают на число точек, входящих в состав динамического ряда –  , а признаки
, а признаки  и
и  суммируются по области исследования.
суммируются по области исследования. , (5.6)
, (5.6)
 , (5.7)
, (5.7)
 , (5.8)
, (5.8)
 .
. , (5.10)
, (5.10) , (5.11)
, (5.11) ,
,  ,
,  – соответственно факториальная, остаточная и общая
– соответственно факториальная, остаточная и общая
 , (5.12)
, (5.12) , (5.13)
, (5.13) , (5.14)
, (5.14) – количество элементов временного ряда;
– количество элементов временного ряда; – количество параметров в уравнении прогнозирующей функции;
– количество параметров в уравнении прогнозирующей функции; ,
,  ,
,  – степени свободы дисперсий.
– степени свободы дисперсий. с
с 
 и
и  при определенных вероятностях.
при определенных вероятностях. ;
; ;
; ;
; возможны следующие ситуации:
возможны следующие ситуации: – уравнение тренда с достаточной точностью описывает расположение исходных данных;
– уравнение тренда с достаточной точностью описывает расположение исходных данных; – точность аппроксимации не обеспечивает необходимую точность – следует перейти к поиску уравнений тренда другой формы.
– точность аппроксимации не обеспечивает необходимую точность – следует перейти к поиску уравнений тренда другой формы. максимальный.
максимальный. необходимо проверить статистическую значимость параметров уравнения тренда.
необходимо проверить статистическую значимость параметров уравнения тренда. проверка статистической значимости параметров выполняется по следующему алгоритму:
проверка статистической значимости параметров выполняется по следующему алгоритму: , (5.15)
, (5.15) , (5.16)
, (5.16) ,
,  – соответственно случайные ошибки параметров
– соответственно случайные ошибки параметров  и
и  – остаточное среднеквадратическое отклонение.
– остаточное среднеквадратическое отклонение. для параметров
для параметров  , (5.17)
, (5.17) , (5.18)
, (5.18) сравнивают с табличными значениями, которые определяют по специальным таблицам для определенной доверительной вероятности, рассчитав предварительно степень свободы
сравнивают с табличными значениями, которые определяют по специальным таблицам для определенной доверительной вероятности, рассчитав предварительно степень свободы  .
.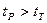 считается, что параметры
считается, что параметры  ,. необходимо расширить область исследования и исследования провести вновь.
,. необходимо расширить область исследования и исследования провести вновь. , (5.19)
, (5.19) – соответственно ординаты на верхней и нижней граничных кривых
– соответственно ординаты на верхней и нижней граничных кривых – расчетное значение признака при вариациях аргумента (фактора
– расчетное значение признака при вариациях аргумента (фактора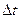 –доверительный интервал.
–доверительный интервал. , (5.20)
, (5.20) , (5.21)
, (5.21) , (5.22)
, (5.22)


