Тема №6 Авторегрессионые методы прогнозирования
Значительная часть социально–экономических явлений развиваются по закономерностям стационарно–случайных процессов. Наиболее часто подобное можно наблюдать при анализе временных рядов, отражающих динамику спроса на продукты питания, объемов хранения сырьевых ресурсов и готовой продукции на предприятиях. В таких рядах, как правило, за количественным ростом или снижением закономерно наступает тенденция обратного характера, подтверждая тем самым наличие зависимости между элементами ряда. Уравнение, выражающее зависимость переменной В практике прогнозирования наиболее часто применяются уравнения авторегрессии в линейной форме. В зависимости от количества элементов, включенных в правую часть, уравнения авторегрессии классифицируются на уравнения 1, 2–го и более высокого порядка. Примеры подобных уравнений приведены ниже:
Общим условием, благодаря которому можно применять метод авторегрессии в прогнозировании, является наличие статистической связи между соседними уровнями динамического ряда. Такое взаимодействие элементов динамического ряда представляет частный случай корреляционной зависимости и называется автокорреляцией. Расчёт прогнозов на основе авторегрессионных моделей выполняется по следующему алгоритму: 1) устанавливают порядок уравнения авторегрессии; 2) рассчитывают параметры выбранной модели авторегрессии; 3) определяют прогноз признака и оценивают его точность. Прежде чем приступить к определению порядка уравнения авторегрессии, необходимо выявить наличие или отсутствие автокорреляции между элементами, отстоящими друг от друга на различные периоды запаздывания. При наличии автокорреляции попутно устанавливается и ее форма. Для отработки данного вопроса на координатное поле наносят пары значений разных элементов:
Интервалы времени Период запаздывания По характеру распределения точек на координатном поле, устанавливают между какими элементами ряда действует корреляционная связь. Автокорреляционное взаимодействие элементов динамического ряда по мере увеличения продолжительности периодов запаздывания уменьшается, разброс точек на координатном поле возрастает. Оценка уровня тесноты автокорреляционной связи выполняется по коэффициенту автокорреляции
где
Перечисленные составляющие при расчете коэффициента автокорреляции рассчитывают по формулам:
где
Среднее значение признака рассчитывается по формуле простой среднеарифметической величины:
Рассчитав, несколько коэффициентов автокорреляция, проранжировав их в зависимости от увеличения периодов запаздывания Для окончательного определения порядка уравнения авторегрессионной функции применяется частная автокорреляционная функция. Использование этой функции основано на признании того факта, что коэффициенты авторегрессии принимают лишь в начале последовательности ненулевые значения. Коэффициенты авторегрессии более высокого порядка стремятся к нулю Введем двойные подстрочные индексы коэффициентам авторегрессии, которые показывают: 1) первый – общее число включенных в уравнение коэффициентов авторегресии; 2) второй – порядковый номер коэффициента авторегрессии в уравнении. После подобных преобразований система уравнений имеет следующий вид:
По мере увеличения порядка уравнения авторегрессии абсолютная величина коэффициента авторегрессии Зависимость коэффициентов авторегрессии от периодов запаздывания Порядок уравнения авторегрессии с помощью частной автокорреляционной функции устанавливают следующим образом: – рассчитывают коэффициенты авторегрессии – ранжируют коэффициенты авторегрессии – анализируют значения коэффициентов авторегрессии по мере роста периодов запаздывания. Коэффициент авторегрессии, существенно отличающийся от нуля, определяет порядок уравнения авторегрессии. Коэффициенты авторегрессии можно рассчитывать одним из способов: методом наименьших квадратов или приближенным методом. Первый способ более подробно будет рассмотрен ниже, рассмотрим второй. По второму способу расчеты ведутся с применением ряда формул:
Для
Предположим, что на основе анализа частной автокорреляционной функции был установлен порядок уравнения авторегрессии, равный трем.
После определения порядка уравнения авторегрессии необходимо рассчитать его параметры. На примере модели (14) рассмотрим порядок расчета параметров способом наименьших квадратов, предусматривающий построение и решение системы нормальных уравнений. Система нормальных уравнений для модели (6.14) имеет следующий вид:
После нахождения параметров прогнозирующей функции и записи ее в конкретном виде приступают к расчету прогнозов в несколько этапов: – на первом этапе рассчитывают значение переменной Для этого в уравнение авторегрессии необходимо подставить такое количество последних элементов динамического ряда, которое равно порядку авторегрессионной модели; – на втором этапе рассчитывают значение признака на момент времени Для оценки точности прогноза можно использовать ряд статистических показателей. Наибольшее распространение получил показатель абсолютного среднего отклонения
где ряда;
Вычисления
|

 , для времени
, для времени  через значения этой же переменной, но в моменты времени
через значения этой же переменной, но в моменты времени  ,
,  , …
, …  называется уравнением авторегрессии.
называется уравнением авторегрессии. , (6.1)
, (6.1) , (6.2)
, (6.2) , (6.3)
, (6.3)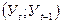 ;
;  ; …;
; …;  , (6.4)
, (6.4) , где
, где  изменяется в пределах
изменяется в пределах  , характеризуют удаленность сравниваемых уравнений динамического ряда и называются продолжительностью запаздывания.
, характеризуют удаленность сравниваемых уравнений динамического ряда и называются продолжительностью запаздывания. ;
;  ; …
; … 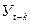 окажут воздействие на переменную
окажут воздействие на переменную  , расчет которого выполняют по формуле:
, расчет которого выполняют по формуле: , (6.5)
, (6.5) – коэффициент автоковариации;
– коэффициент автоковариации; – общая дисперсия ряда.
– общая дисперсия ряда. , (6.6)
, (6.6)
 , (6.7)
, (6.7) – значения элементов ряда;
– значения элементов ряда; – значения элементов ряда, смещенных относительно точки
– значения элементов ряда, смещенных относительно точки 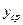 – среднее значение признака;
– среднее значение признака; – число элементов ряда.
– число элементов ряда.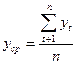 , (6.8)
, (6.8) , можно получить автокорреляционную функцию. Автокорреляционная функция, как нетрудно догадаться, характеризует зависимость коэффициентов автокорреляции от продолжительности периодов запаздывания
, можно получить автокорреляционную функцию. Автокорреляционная функция, как нетрудно догадаться, характеризует зависимость коэффициентов автокорреляции от продолжительности периодов запаздывания  . С помощью этой функции выполняется качественная оценка порядка уравнения авторегрессии. Автокорреляционную функцию, как правило, исследуют в следующем интервале области исследования
. С помощью этой функции выполняется качественная оценка порядка уравнения авторегрессии. Автокорреляционную функцию, как правило, исследуют в следующем интервале области исследования  , подтверждая тем самым снижение степени влияния более отдалённых элементов от точки
, подтверждая тем самым снижение степени влияния более отдалённых элементов от точки  , (6.9)
, (6.9) , (6.10)
, (6.10) , (6.11)
, (6.11) уменьшается.
уменьшается. с разными периодами запаздывания;
с разными периодами запаздывания;
 , (6.12)
, (6.12) , (6.13)
, (6.13) , (6.14)
, (6.14) , (6.15)
, (6.15) для времени.
для времени. : при
: при 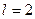 ;
;  и т.д.
и т.д. , расчет которого выполняют по формуле:
, расчет которого выполняют по формуле: , (6.16)
, (6.16) – порядок прогнозирующего уравнения авторегрессии;
– порядок прогнозирующего уравнения авторегрессии; – период упреждения, на который рассчитывается прогноз.
– период упреждения, на который рассчитывается прогноз.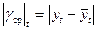
 ,
,


