Задача№1. По исходным данным, характеризующим месячную отгрузку пищевой продукции за десять месяцев, необходимо:
По исходным данным, характеризующим месячную отгрузку пищевой продукции за десять месяцев, необходимо: – установить наличие или отсутствие автокорреляции между уровнями динамического ряда, отстоящими друг от друга на I, 2 и 3 периода запаздывания; – рассчитать коэффициенты автокорреляции и авторегрессии и проанализировать автокорреляционную и частную автокорреляционную функции на предмет установления порядка уравнения авторегрессии; – рассчитать параметры уравнения авторегрессии и записать прогнозирующую функцию в конкретном виде; – рассчитать прогнозы с периодами упреждения – разработать экономическую стратегию фирмы, исходя из ее рыночной ситуации. Таблица 1 – Исходные данные
Решение: Рассчитаем среднемесячную отгрузку продукции по формуле (6.8)
Необходимо исследовать наличие или отсутствие автокорреляции между элементами, отстоящими друг от друга на 1, 2 и 3 периода запаздывания: Конкретные значения элементов, входящих в соответствующие пары, приведены ниже.
Для всех значения элементов, входящих в соответствующие пары ясно прослеживается упорядоченность расположения точек на координатном поле, что свидетельствует о наличии достаточно прочной автокорреляционной связи между элементами с анализируемыми периодами запаздывания. Кроме наличия автокорреляционной связи можно определить форму этой связи, которая, выступает в двух видах: прямой и обратной. Прямая форма автокорреляционной связи наблюдается между элементами в том случае, когда образуется правый угол наклона между линией, проведенной через середину области расположения точек, и линией параллельной оси абсцисс и обратная при левом угле наклона. При отсутствии упорядоченности в расположении точек на координатном поле напрашивается вывод об отсутствии или незначительной автокорреляционной связи между соответствующими элементами. После отработки этапа по оценке наличия или отсутствия автокорреляционной связи приступают к выявлению порядка уравнения авторегрессии. Для выявления порядка авторегрессионной модели необходимо исследовать автокорреляционную и частную автокорреляционную функции. С этой целью необходимо рассчитать общую дисперсию, коэффициенты автоковариации и коэффициенты автокорреляции. В таблице 2 представлены все необходимые составляющие для расчета вышеперечисленных статистических показателей. Коэффициенты автокорреляции, характеризующие тесноту связи между элементами с разными периодами запаздывания, имеют следующие значения:
Таблица 3 – Расчет необходимых компонентов для определения
Некоторые пояснения к расчету коэффициентов автокорреляции. В формулу подставим выражения, по которым вычисляются компоненты Благодаря такому преобразованию расчетные значения Таблица 3– Зависимость коэффициента автокорреляции от периодов запаздываний.
Совокупность Автокорреляционная зависимость дает возможность выполнить качественную оценку порядка уравнения авторегрессии. Для рассматриваемого динамического ряда можно высказать предположение, что прогнозирующая модель, вероятно, может быть представлена уравнением авторегрессии второго или третьего порядка. Для уточнения порядка уравнении авторегрессии необходимо использовать частную автокорреляционную функцию, как отмечалось выше, выражающую зависимость коэффициента авторегрессии Ниже приведен расчет коэффициентов авторегрессии вторым способом, использованы формулы:
Таблица 3– Зависимость коэффициента автокорреляции от периодов запаздывания.
Анализ полученной зависимости свидетельствует о том, что частная автокорреляционная функция имеет резкий спад после
Для нахождения параметров прогнозирующей модели воспользуемся методом наименьших квадратов, который, как известно, связан с построением и решением системы нормальных, уравнений. Применительно к нашему примеру система нормальных уравнений представлена следующими выражениями:
Для того, чтобы представить систему нормальных уравнений конкретными выражениями, расчет необходимых компонентов выполнен в таблице 4. Подставив, соответствующие значения компонентов в систему нормальных уравнений, получим:
Решение данной системы можно выполнить любым способом. Ниже приведен ее решения способом исключения одного из неизвестных.
Таблица 4 – Расчет необходимых компонентов для системы нормальных уравнений
Избавимся от неизвестного «а2», для чего умножим все элементы первого уравнения на коэффициент, равный отношению
– _________________________
Ниже приведен расчет второго неизвестного «а1», путем простой подставки найденного значения первого параметра – «а2».
Уравнение авторегрессии, выполняющего функцию прогнозирующей модели, имеет вид:
Определим месячные объемы отгрузки производства в ноябре–декабре текущего года и в январе следующего года, то есть при По уравнению авторегрессии (27) рассчитаем отгрузку продукции в соответствующие месяцы:
Найдем абсолютную среднюю ошибку прогнозов (см.формулу 16) с упреждениями
Таблица 5– Расчет абсолютного среднего отклонения
Анализ средних абсолютных отклонений (см. таблицу 5) позволяет сделать вывод, что наименьшая погрешность вычислений наблюдается в случае выполнения расчетов при В дальнейшем, по мере роста продолжительности периодов запаздывания эта тенденция сохраняется. Нарушение тенденции на участках с периодами запаздывания Рассчитав наиболее вероятные объемы отгрузки продукции на ближайшие месяцы, необходимо оценить положение предприятия на рынке. Согласно маркетинговым исследованиям было установлено, рыночная доля предприятия 40 % при уровне насыщения рынка аналогичной продукцией на 101 %. Средний объем отгрузки продукции» на ближайшие месяцы составит:
Следовательно, для полного удовлетворения потребностей необходимо в целом поставить продукции в количестве:
а с учетом установившегося соотношения между спросом и предложением:
Располагая этими данными, необходимо разработать определенную организационно–экономическую стратегию предприятия. Применительно к рассматриваемому примеру можно разработать одну из перечисленных стратегий: – товарная стратегия (стратегическая сегментация внешней и внутренней среды фирмы; выделение стратегических зон хозяйствования; выбор позиции в конкуренции; оценка привлекательности стратегической зоны хозяйствования; формирование товарного ассортимента); – стратегия ценообразования (ценовая политика и методы определения цен; определение цен и предпочтительных объемов производства на основе равенства предельного дохода предельным издержкам); – стратегия взаимодействия фирмы с рынками производственных ресурсов (характеристика рынков факторов производства; принципы эффективного распределения ресурсов; факторы, определяющие спрос на ресурсы со стороны производственной системы) – стратегия снижения производственных издержек (стратегия получения конкурентных преимуществ за счет снижения затрат; достижение конкурентных преимуществ через лидерство в низкой стоимости продукций); – стратегия стимулирования персонала фирмы (кадровые ресурсы фирмы; система оплаты труда работников службы маркетинга).
|

 ;
; 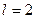 ;
;  и оценить точность прогнозов с помощью абсолютного среднего отклонения
и оценить точность прогнозов с помощью абсолютного среднего отклонения  ;
;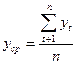 , (6.8)
, (6.8) тыс.т.
тыс.т. ;
;  ;
;  .
.

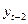


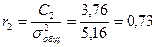
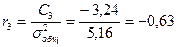

 ,
,  и
и 

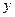



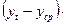
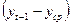
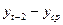


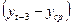




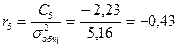
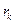 можно получить непосредственно по данным таблицы 3.
можно получить непосредственно по данным таблицы 3.
 от периода запаздывания
от периода запаздывания  , (6.12)
, (6.12)
 , (6.13)
, (6.13)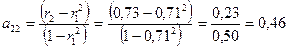
 , (6.14)
, (6.14)
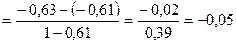
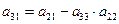 , (6.18)
, (6.18)
 , (6.19)
, (6.19)
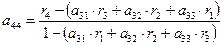 , (6.20)
, (6.20)

 , (6.21)
, (6.21)
 , (6.22)
, (6.22)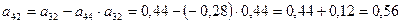
 , (6.23)
, (6.23)
 , (6.24)
, (6.24)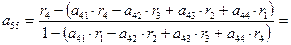

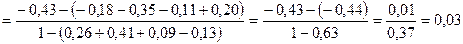

 . Такая ситуация свидетельствует о возможности использования прогнозирующей (прогнозной) модели в форме двухчленного уравнения авторегрессии.
. Такая ситуация свидетельствует о возможности использования прогнозирующей (прогнозной) модели в форме двухчленного уравнения авторегрессии.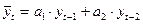 , (6.25)
, (6.25) , (6.26)
, (6.26)






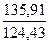 .
.






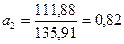
 , (6.27)
, (6.27) ,
, 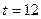 и
и  .
. тыс.т.
тыс.т. тыс.т.
тыс.т. тыс.т.
тыс.т. , (16)
, (16)
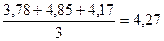 тыс.т.
тыс.т.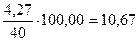 тыс.т.
тыс.т.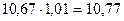 тыс.т.
тыс.т.


