Примеры решения задач
6-1п. В краткосрочном периоде фирма может изменять величину используемых трудовых ресурсов, но не может влиять на величину используемого капитала. Таблица 6-1 показывает, как может изменяться выпуск продукции вследствие изменения объемов применяемого труда. Таблица 6-1
а) Определите средний продукт труда (APL) и предельный продукт труда (MPL). Полученные результаты впишите в таблицу. б) Предположим, что менеджер фирмы решил заменить старое оборудование новым, более эффективным. Изменится ли при этом положение кривых APL и MPL. Аргументируйте ваш ответ.
Решение а) Величина среднего продукта переменного фактора (АР), в данном случае труда, определяется по формуле: б) Положение кривых APL и MPL изменится, так как каждая единица труда будет приносить больший результат. В итоге кривые сместятся вверх и, возможно, изменят свою форму. Таблица 6-2
6-2п. Максимизировать выпуск при фиксированных затратах, если на сегодня положение представлено в таблице 6-3. Таблица 6-3
а) в мгновенном периоде; б) в краткосрочном периоде при фиксированных затратах капитала и неизменных ценах; в) в долгосрочном периоде.
Решение а) В мгновенном периоде изменить ничего нельзя, и потому максимум совпадает с существующим положением: LК+2L+4К=48+12+32=92. б) В краткосрочном периоде при фиксированных затратах капитала и неизменных ценах результат будет, очевидно, тем же: Q=Qmах=92. в) В долгосрочном периоде начинается настоящая оптимизация, так как подвижными становятся и затраты труда, и затраты капитала. Необходимо решить задачу на максимум функции LК+2L+4К → Мax при 10L+5К=100. Подставим вытекающее из ограничения выражение К=20-2L в максимизируемую функцию и получим стандартную математическую задачу на максимум квадратичной функции L(20-2L)+40-8L+2L. Приравняв производную этой квадратичной функции к нулю, получим 14-4L=0, т. е. L=3, 5; К=13. В результате Qmax=104, 5. Ответ: При условиях а) и б) положение останется без изменений, Q=Qmax=92. в) L=3, 5, К=13, Qmax=104, 5.
6-3п. Найдите точки, принадлежащие изокванте с уровнем выпуска, равным 100, по данным о производственной функции Q(L, К), представленным в таблице 6-4. Таблица 6-4
Решение
Изокванта Q=100 содержит точки, приведенные в таблице 6-5. Таблица 6-5
Ответ: Изокванте с уровнем выпуска 100 принадлежат точки: (L=10, К=50), (L=20, К=30), (L=30, К=20), (L=50, К=10).
6-4п. Производственная функция Q=5L0, 5K, где L – расход труда, К – расход капитала. Найдите предельный продукт капитала, если расход труда равен 4, расход капитала равен 7.
Решение
В теории производства традиционно используется двухфакторная производственная функция вида Q=f(L, К) и чаще всего так называемая функция Кобба-Дугласа, В общем виде она записывается следующим образом: Q=a0Lа1Kа2, где L – затраты труда; К – затраты капитала; а0 – коэффициент пропорциональности; a1 – коэффициент эластичности выпуска по труду; а2 – коэффициент эластичности выпуска по капиталу. Коэффициенты а1 и а2 характеризуют относительный прирост выпуска продукции на единицу относительного прироста затрат труда (L) и капитала (К)соответственно. Предельный продукт переменного фактора производства, в данном случае капитала (МРК) – это дополнительный выпуск продукции, вызванный применением одной дополнительной единицы переменного ресурса (капитала):
Если Q=5L0, 5K и L=4, а К=7, то МРК = 5L0, 5= 5 х 2 = 10.
Ответ: МРК = 10.
6-5п. Производственная функция Q=5L0, 8K0, 2. Издержки производителя равны 30. Цена труда 4, капитала 5. Найдите равновесный расход ресурсов.
Решение а) MRTS=0, 81L-0, 2К0, 2/0, 2L0, 8K-0, 8, или MRTS=4K/L; б) в точке равновесия 4K/L=4/5; в) запишем уравнение изокосты: 4L+5К=30; г) составим систему уравнений, взятых из пунктов 2 и 3, ее решение: L=6, К=1, 2 – равновесный расход ресурсов.
Ответ: L=6, К=1, 2. 6-6п. Подсчитайте средний и предельный продукт фирмы, если известны следующие данные (таблица 6-6): Таблица 6-6
Когда начинает действовать в данном случае убывающая экономия от масштаба? Решение
Если число рабочих – это затраты труда L, а совокупный продукт – Q, то APL=Q/L; MPL=(Qi-Qi-1). Таблица 6-7
Экономия от масштаба начинает снижаться после того, как число работников превысит 2. Ответ: убывающая экономия от масштаба начинает действовать после найма второго работника. 6-7п. Фирма использует в производстве товара капитал (К) и труд (L), при этом МРК=8, a MPL=20. Цены единиц факторов: Рк=4; PL=10. Является ли оптимальным использование ресурсов фирмой с точки зрения минимизации издержек? Решение Правило минимизации издержек для каждого заданного объема выпуска продукции следующее: оптимальное сочетание факторов, используемых в процессе производства, достигается тогда, когда последний затраченный рубль на покупку каждого фактора дает одинаковый прирост общего выпуска продукции. То есть Ответ: использование ресурсов фирмой является оптимальным. 6-8п. Производственная функция фирмы равна Q=K1/4L3/4. Цена капитала равна 4 тыс. руб. Цена труда равна 12 тыс. руб. Какое количество капитала и труда должна иметь фирма для выпуска 300 тыс. единиц? Решение
K1/4L3/4=300. Решаем систему и получаем: К = 300; L = 300. Ответ: К = 300; L = 300.
6-9п. Почему средний продукт труда продолжает увеличиваться после прохождения точки начала уменьшения предельной производительности? Решение
6-10п. Предположим, что фирма увеличивает капитал со 100 до 150 единиц, труд – с 400 до 600 единиц. Выпуск продукции при этом возрастает с 300 до 350 единиц. Какова в данном случае будет отдача от масштаба (возрастающая, постоянная или убывающая)? Решение
Эффект масштаба проявляется в снижении долговременных средних издержек производства на единицу продукции. Первоначальное соотношение труда и капитала составляло: 400/100 = 4/1. Затем капитал увеличился на (150 - 100)/100 = 1/2; труд на (600 - 400)/400 = 1/2. Выпуск продукции возрос на (350 - 300)/300 = 1/6. То есть имеет место отрицательный эффект масштаба (рис. 33.).
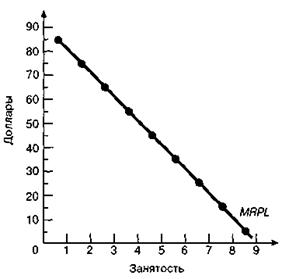
Рис. 33. Ответ: отрицательный эффект масштаба. 6-11п. В таблице 6-10 представлена основная информация о производстве фирмы при найме переменного количества труда и фиксированном количестве капитала. а) Рассчитайте предельный продукт труда (МРL). б) Если продукт может быть продан на рынке по цене 5 долл. за единицу, рассчитайте TR и впишите в таблицу 6-8. Рассчитайте также и впишите значения MRPL. в) Начертите кривую MRPL фирмы. По вертикальной оси откладывайте значение MRPL в долл., а по горизонтальной – занятость. Нанесите предельные значения шкалы на равном расстоянии от средних точек в интервалах шкалы горизонтальной оси. Таблица 6-10
г) Используя полученные данные, заполните графу спроса фирмы на труд в таблицу 6-11. Есть ли какая-либо разница между кривой MRPL фирмы и кривой спроса на труд? Таблица 6-11
Решение
Величина предельного продукта труда (МРL) рассчитывается по формуле: А совокупный доход по следующей формуле:
где Р – цена продукта (долл.), Q – совокупный выпуск (шт.). Предельная доходность труда определяется следующим образом:
Заполним таблицу 6-12 целиком. а, б) Таблица 6-12
в) Кривая MRPL фирмы приведена на рисунке 34.
Рис. 34. Отрицательный наклон кривой MRPL связан с действием закона убывающей предельной производительности фактора, а ее расположение определяется уровнем предельной производительности фактора (MPL) и ценой произведенного продукта (Р).
г) Кривая спроса фирмы на один переменный фактор (L) совпадает с кривой его предельного продукта в денежной форме (MRPL), так как любая точка на данной кривой показывает число занятых, используемых фирмой при каждом заданном уровне ставки заработной платы (w). Таблица 6-13
Ответ: а, б) МРL: 17, 15, 13, 11, 9, 7, 5, 3, 1; TR: 0, 85, 160, 225, 280, 325, 360, 385, 400, 405; MRPL: 85, 75, 65, 55, 45, 35, 25, 15, 5. г) DL: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. кривая спроса фирмы на один переменный фактор (L) совпадает с кривой его предельного продукта в денежной форме (MRPL).
|

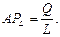 Авеличина предельного продукта переменного фактора (МР) (труда) рассчитывается следующим образом:
Авеличина предельного продукта переменного фактора (МР) (труда) рассчитывается следующим образом: 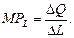
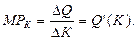



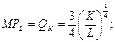




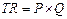 ,
,