Задания для практических занятий и самостоятельной работы. 5-1з. Общая и предельная полезности (TU и MU соответственно) товаров А, В, С представлены в таблице 5-5
5-1з. Общая и предельная полезности (TU и MU соответственно) товаров А, В, С представлены в таблице 5-5. Заполните пропуски в таблице. Таблица 5-5
5-2з. Постройте кривую безразличия, проходящую через точки: Таблица 5-6
Определите с помощью построения бюджетной линии минимальный бюджет (равновесие потребителя) при следующих ценах: РY=3 руб. и PX = 1 руб.
5-3з. Бюджетная линия проходит через точки Y=45; X=0 и Y=0; Х=75. Цена единицы товара Х составляет 6 рублей. Каков бюджет потребителя? Какова цена товара Y? Напишите уравнение бюджетной прямой. Каков наклон бюджетной линии к оси абсцисс? Как изменится положение бюджетной линии, если цена на товар Y увеличится на 2 руб. за единицу товара?
5-4з. Построить кривую безразличия для двух абсолютно взаимозаменяемых товаров пепси-колы и кока-колы, если их цены за литр равны 8 и 10 руб. при бюджете на их потребление, равном 40 руб. 5-5з. Построить линию бюджетного ограничения для двух взаимозаменяемых товаров при доходе потребителя, равном 900 денежным единицам. Цена продукта А – 10 единиц, а продукта Б – 20 единиц. Как сместится линия при снижении цены продукта Б на 10%? 5-6з. На рисунке 29 изображена одна из кривых безразличия потребителя и его бюджетная линия.
Рис. 29. Задание: а) определите доход потребителя при цене товара Y, равной 40 руб.; б) определите цену товара X; в) напишите уравнение бюджетной линии; г) постройте бюджетную линию при условии, что цена товара Y возрастет до 45 руб. 5-7з. Применяя правило максимизации полезности, определите комбинацию товаров А и В, максимизирующую полезность при доходе, равном 14 долл. Если Ра=1 долл., Рв=2 долл. Таблица 5-8
5-8з. Предположим, что предельная полезность видеокассеты равна 45 ютилям, а просмотра кинофильма – 30 ютилям. Видеокассета стоит 3 долл., а билет в кино – 1, 5 долл. Применяя правило максимизации полезности, в пользу чего вы сделаете выбор?
5-9з. Доход Александры составляет 200 долл. в неделю. Она живет в простом мире, в котором существуют только два вида ограниченных благ: говядина и рубашки. Фунт говядины стоит 5 долл., а каждая рубашка 20 долл. a) Составьте таблицу 5-7, указывающую пять потребительских пар, которые Александра может себе позволить. б) Постройте график бюджетного ограничения Александры и напишите уравнение бюджетной линии. в) Как изменилось бы бюджетное ограничение Александры, если бы цена говядины упала до 4 долл. за фунт, цена рубашек – до 18 долл. за штуку, а ее доход – до 180 долл. в неделю? Таблица 5-7 Альтернативные, допустимые потребительские варианты (пары)
5-10з. В набор потребителя входят пиво (П) и раки (Р). Бюджет потребителя равен 14 у.е. Заполните пустующие клеточки в нижеследующей таблице 5-9. Таблица 5-9
а) Постройте кривые общей (TUП) и предельной (MUП) полезности пива. б) Постройте кривые общей (TUР) и предельной (MUР) полезности раков. в) Если цена одной банки пива 2 у.е., а цена одного рака 1 у.е., определите при каком соотношении данных товаров максимизируется общая полезность набора, состоящего из пива и раков. 5-11з. Предположим, что доход потребителя равен 2400 р. Домашнее хозяйство потребляет товары Х и Y. Их цены соответственно равны 400 и 600 р. Значения предельной полезности приведены в таблице 5-10. Определите при каком соотношении товаров максимизируется общая полезность, а также общую полезность в точке равновесия. Таблица 5-10
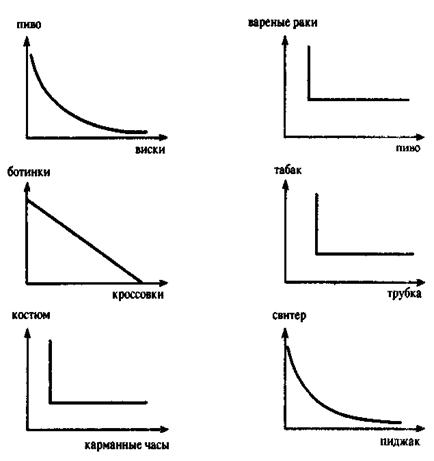
5-13з. В небольшом городке на юге Англии неизвестный преступник ограбил ночью магазин. Похоже, что это ограбление было не первым в его жизни – он не оставил ни отпечатков пальцев, ни окурков сигарет и, к огорчению Скотланд-Ярда, преступника никто не видел Эксперт-экономист узнав, что именно украдено, нарисовал несколько карт безразличия, отражающих вкусы преступника (рис. 31.). Пользуясь «дедуктивным методом» Шерлока Холмса и своими знаниями микроэкономики, напишите портрет преступника.
Рис. 31. 5-14з. У потребителя есть три альтернативных способа использования сливочного масла: для бутербродов, в кашу и для выпечки торта. Данные об общей полезности от потребления масла приведены в таблице 5-11. Таблица 5-11
Имея в неделю 400 гр. масла, какое максимальное количество общей полезности может получить потребитель, если использует масло только на три эти продукта?
5-15з. Марта может расходовать каждую неделю 150 у.е. дохода. Она покупает молоко и хлеб. Допустим, что пакет молока стоит 2, 5 у.е., а цена буханки хлеба – 1 у.е. а) начертите линию бюджетного ограничения Марты; какова возможная стоимость дополнительной буханки хлеба, выраженная в стоимости пакета молока; б) допустим, что в период инфляции стоимость буханки хлеба увеличилась до 1, 5 у.е. за ед., а стоимость пакета молока осталась той же; начертите новую линию бюджетного ограничения; какова возможная стоимость дополнительной буханки хлеба в новых условиях; в) допустим, что с учетом темпов инфляции Марте повысили заработную плату, и теперь она может расходовать 225 у.е. в месяц; начертите новую линию ее бюджетного ограничения; какова возможная стоимость дополнительной буханки хлеба в новых условиях. 5-16з. Паула тратит весь свой доход на просмотр спектаклей и фильмов, и удовлетворение от спектаклей она оценивает в 2 раза выше, чем от фильмов. а) Начертите ее карту безразличия. б) Паула зарабатывает 120 долл. в неделю. С учетом того, что цена каждого билета на спектакль составляет 12 долл., а на фильм – 4 долл., начертите линию ее бюджетного ограничения и наивысшую достижимую кривую безразличия. Сколько спектаклей сможет посмотреть Паула? в) Если билет на спектакль стоит 12 долл., а билет на фильм – 5 долл., сколько спектаклей сможет посмотреть Паула? 5-17з. Расходы Бориса на его утренний кофе с молоком составляют 9 долл. в неделю. Он любит кофе, приготовленный в соотношении 4 части кофе на 1 часть молока. Стоимость кофе – 1 долл. за унцию, а стоимость молока – 0, 5 долл. за унцию. Сколько кофе и сколько молока будет покупать Борис в неделю? Изменятся ли ваши ответы, если цена на кофе увеличится до 3, 25 долл. за унцию? Представьте ваши ответа графически. 5-18з. Бюджетная линия Ивана пересекает одну из его кривых безразличия в точках с координатами: у1=6; х1=2; у2=2; х2=4. Определить бюджет Ивана, если известно, что цена товара Y равна 3 ден. ед. 5-19з. Господин Иванов съедает за месяц 1, 5 кг свинины по 65 руб. за килограмм и 1 кг говядины по 90 руб. за килограмм, считая такое положение дел вполне удовлетворительным. В каком соотношении он оценивает предельную полезность от потребления свинины к говядине?
5-20з. Потребитель находится в состоянии равновесия при следующей структуре его покупок: 2 кг овощей по 3 д. ед. за килограмм и 4 кг фруктов по 5 д. ед. Определите предельную норму замещения фруктов овощами и бюджетное ограничение потребителя. 5-21з. Господин Шалимов выпивает в неделю 15 чашек чая, тратя на каждую чашку 1, 5 руб., и 10 чашек кофе, тратя на каждую чашку 3 руб. В каком соотношении он оценивает предельную полезность от потребления кофе к чаю? 5-22з. Бетти имеет недельный резерв в размере 6 долл., который она тратит на комиксы (k) и шоколад (s). Каждая книга комиксов стоит 2 долл., а каждая шоколадка – 1 долл. Полезность для Бетти каждую неделю складывается из совокупной полезности от комиксов (TUk) и совокупной полезности от шоколада (TUs). Две составляющие ее функции, совокупной полезности представляются следующим образом: Таблица 5-12
а) Показывает ли функция полезности Бетти убывающую предельную полезность от комиксов? б) Какую комбинацию благ выберет Бетти? в) Покажите, что для Бетти не оптимальна трата всего свободного остатка денег на комиксы. г) Покажите, что также не оптимальна для Бетти трата всего ее резерва на конфеты.
5-23з. Бюджетная линия задана уравнением: Таблица 5-13
5-24з. Постройте кривые безразличия Алеши и Наташи для двух благ: арбузов и яблок при условии, что Алеша любит яблоки и не ест арбузов, а Наташа с удовольствием ест арбузы и ненавидит яблоки. 5-25. Винни-Пух получает следующую общую полезность (TU) от потребления мороженого и варенья независимо друг от друга (таблица 5-14), т. е. Винни-Пух настолько большой сластена, что получает одно и то же удовольствие от мороженого независимо от того, сколько он уже съел варенья, и наоборот. Таблица 5-14
а) Найдите предельную полезность потребления мороженого и варенья. б) Винни-Пух может потратить на мороженое и варенье 102 кроны, а их цены 9 крон за порцию и 11 крон за 100 г соответственно. Какая комбинация мороженого и варенья будет максимизировать полезность? в) Какова будет оптимальная комбинация, если Винни-Пух вдруг станет миллионером и его расходы на такие «приоритеты», как мороженое и варенье, не будут ничем ограничены?
5-26з. Постройте карты кривых безразличия полезности для двух абсолютно взаимодополняющих товаров в пропорции 3: 1 и для двух абсолютно взаимозаменяемых видов товаров (с некоторой натяжкой это могут быть мандарины и апельсины, тонкие тетради в клетку и тетради потолще и т. п.) в той же пропорции 3: 1.
5-27з. Чему равна предельная полезность товара В в состоянии равновесия потребителя, если потребитель приобретает два товара: А и В, причем предельная полезность товара A – 100 ют.; цена товара А – 10 ден. ед.; цена товара В – 5 ден. ед.?
5-28з. Семья покупает 100 кг сахара в год по цене 4 р. за килограмм. При увеличении цены сахара до 4, 5 р. определить: а) Как изменится потребление сахара данной семьи? б) Как изменятся расходы на потребление сахара, если известно, что эластичность спроса на сахар по цене у данной семьи равна 1, 5? в) Определить, какую предельную полезность получала семья, потребляя сахар по 4 р. за 1 кг, если предельная полезность яблок по цене 10 р. за 1 кг для данной семьи составляет 5 и семья оптимально распределяет свои денежные средства? г) Какую предельную полезность получит семья, потребляя сахар по 4, 5 р. за 1 кг? Определите предельную норму замещения сахара на яблоки в первом и во втором случаях. 5-29з. Функция общей полезности потребителя: ТU=QaQb, где Qa и Qb – количество двух благ: А и В. Бюджет потребителя равен 36 д. ед. При сложившихся ценах потребитель поочередно покупает два набора благ Qa=6; Qb=2 и Qa=3; Qb=4, тратя на покупки весь свой бюджет. Определите цену двух благ и равновесие потребителя. 5-30з. Доход потребителя равен 10 у.е., цены товаров Х и Y равны 2 у.е. и 5 у.е. соответственно. Найдите равновесный набор, если функция полезности равна ТU=2х+5у. 5-31з. Вычислить функцию общей полезности по заданной предельной полезности MU(х)=5-х. 5-32з. Функция полезности Владимира имеет вид: ТU=Qa0, 5Qb0, 5. Определить функцию спроса по цене на благо В при бюджете потребителя, равном 30 ден. ед.
5-33з. Дана функция полезности потребителя A: а) Какая из следующих пар товаров наиболее предпочтительна для потребителя А: (5, 1), (2, 3), (1, 7), (3, 2)? б) Если у потребителя В функция полезности
5-34з. Доход потребителя равен 80, цены продуктов X, Y, и Z равны 4, 5 и 2 соответственно. Найдите равновесный набор, если функция общей полезности равна: ТU=12QX+10QY+8QZ. 5-35з. Функция полезности ТU=(х+1)у, доход потребителя – 8, цены продуктов Х и Y равны 4. Найдите равновесный набор. 5-36з. Функция общей полезности потребителя ТU=2XY, где Х – количество покупаемых им видеокассет, Y – количество покупаемых аудиокассет. Его еженедельные расходы на приобретение этих двух товаров составляют 50 руб. Цена видеокассеты – 15 руб., цена аудиокассеты – 5 руб. Определите оптимальный объем еженедельных закупок видео- и аудиокассет. Как изменится спрос на эти товары, если цена видеокассет возрастет до 20 руб.?
5-37з. MU(x)=16/х, MU(y) = 9/y, где х и у – количества благ Х и Y. У вас есть возможность приобрести две единицы любых благ. Какой набор максимизирует вашу полезность? Рх=8, Ру=6. Максимизируйте полезность своего выбора при бюджете в 100 денежных единицы.
5-38з. Функция предельной полезности MU(x)=50-5х выражена в денежных единицах. Найти наилучший объем потребления при цене Р=10. 5-39з. Функция общей полезности потребителя: ТU=QaQb, где Qa и Qb – количество двух благ: А и В по цене 25 и 40 д. ед. соответственно. Бюджет потребителя равен 600 д. ед. Какова должна быть структура покупок в ситуации равновесия потребителя? Насколько возрастет благосостояние потребителя, если цена блага В снизится на 25%? 5-40з. Маша тратит 140 руб. в месяц на персики и клубнику. а) Общая полезность персиков независимо от количества клубники оценивается в б) Предположим, что изменились условия в том, что касается полезности клубники: в) Что будет, если общая полезность персиков и клубники задается формулой 5-41з. Предположим, что молокозавод в небольшом городке Н. вырабатывает только молоко и кефир, который местные жители рассматривают как заменители друг друга. Для того чтобы оценить отношение жителей городка к полезности потребления молочных изделий, можно выделить три варианта потребления в неделю, в каждом из которых жителям абсолютно безразлично, в какой комбинации молока и кефира они будут их потреблять: Таблица 5-15
Какой из предложенных уровней полезности можно оценить как самый высокий, а какой – как самый низкий? Постройте соответствующие кривые безразличия. Допустим, что половина жителей городка Н. работает на заводе, получая примерно одинаковую заработную плату, которая позволяет им тратить на потребление молочных продуктов 90 руб. в неделю. Постройте кривую спроса на кефир каждого из этих жителей при условии, что цена на молоко не изменяется в зависимости от цены на кефир и составляет 10 руб. за пакет (возьмите для примера цены кефира 5; 10; 30 руб. за пакет). Используйте для этого построенные ранее кривые безразличия. а) Сколько пакетов кефира в неделю захочет купить житель городка Н. по цене 15 руб. за пакет? б) Как изменится спрос на кефир при увеличении цены пакета молока до 15 руб.? Проиллюстрируйте ответ при помощи имеющихся кривых безразличия. в) Как изменятся поведение потребителей и спрос на кефир в случае, если молокозавод решит освоить выпуск сметаны? г) Как изменятся поведение потребителей и спрос на кефир, если заработная плата на заводе повысится на столько, что работающие там смогут тратить на молочные продукты 180 руб. в неделю, а цена на молоко останется на прежнем уровне?
|
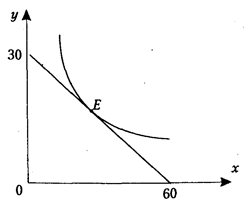
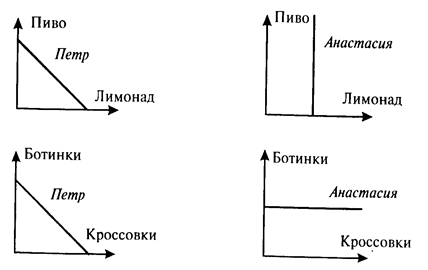Рис. 30.
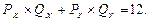Доход потребителя распределяется между двумя товарами Х и Y, при этом РХ=1 у.е., а РY=2 у.е. Каким будет оптимальное сочетание товаров, купленных данным потребителем, если его карта безразличия задана таблицей 5-13.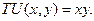
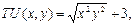х> 0, у> 0, то какая пара из а) предпочтительна для него? В чем разница между потребителями А и В?
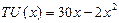, где х – количество килограммов персиков в месяц. Общая полезность клубники также не зависит от наличия персиков и составляет 
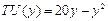, где у – количество килограммов клубники. Цена персиков – 10 руб. за килограмм, а клубники – 20 руб. Сколько купит персиков и клубники рациональная Маша?
.
?
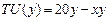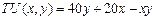