ВИЗНАЧЕННЯ ДОВЖИНИ ХВИЛІ ЛАЗЕРНОГО ВИПРОМІНЮВАННЯ МЕТОДОМ ІНТЕРФЕРЕНЦІЇ СВІТЛА У БІПРИЗМІ ФРЕНЕЛЯ
Мета роботи: Визначити довжину хвилі лазерного випромінювання методом інтерференції світла у біпризмі Френеля. Прилади та обладнання: 1) Оптична лава, яка має лінійку. 2) Лазер. 3) Джерело живлення лазера. 4) Щільова діафрагма (ширина щілини повільно регулюється у межах 0-4 мм). 5) Біпризма Френеля з кутом заломлення ( 6) Короткофокусна збиральна лінза з фокусною відстанню f = 35, 83 мм. 7) Непрозорий екран з горизонтальною та вертикальною шкалами з міліметровими поділками. Опис методу та установки Мета цієї роботи – ознайомлення з явищем інтерференції світлових хвиль у схемі з біпризмою Френеля та вимірювання довжини хвилі лазерного випромінювання інтерференційним методом. · Як джерело світлових коливань використовують лазер ЛГ – 72, який дає вузький пучок (діаметром~1, 5 мм) монохроматичного випромінювання. Потужність лазера 0, 6 мВт. Лазер живиться від джерела ИП-10, яке працює від мережі з напругою 220 В.
Світло від щілини S після заломлення у біпризмі поділяється на два пучки, які перекриваються та виходять із двох уявних зображень щілини S 1 та S 2, є когерентними джерелами. При цьому за призмою на екрані в області перетину пучків спостерігається інтерференційна картина у вигляді світлих і темних ліній, які чергуються та паралельні щілині S, АВ – область інтерференції.
При заданому значенні 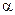 (в нашому випадку (в нашому випадку 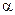 =18¢) відстань між сусідніми світлими лініями =18¢) відстань між сусідніми світлими лініями 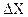 залежить від довжини випромінювання залежить від довжини випромінювання 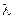 0 і відстані L (рис. 2) від площини, в якій лежать уявні джерела S 1 і S 2 до площини, в якій спостерігається інтерференційна картина (площина МОN). 0 і відстані L (рис. 2) від площини, в якій лежать уявні джерела S 1 і S 2 до площини, в якій спостерігається інтерференційна картина (площина МОN).
Нехай М – точка у площині МОN, відстань МО позначимо через Х, відстань між уявними джерелами S 1 та S 2 – через l, різницю хода променів від S 1 та S 2, тобто S 2 K через Оскільки L > > l, то трикутники МАО і S 1 S 2 K подібні:
Вважаючи, що АМ» L, (що дійсно, якщо X< < L) отримуємо
Оскільки інтерференційні максимуми спостерігаються в тому випадку, якщо
Звідси знаходимо відстань між сусідніми світлими лініями:
Вимірюючи ширину інтерференційних ліній
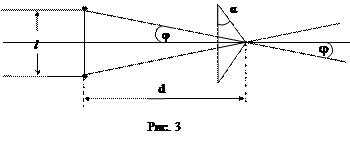
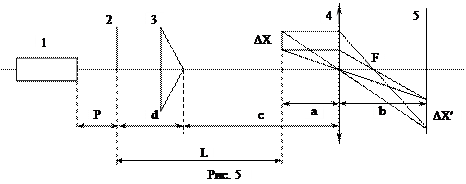
Відстань між уявними джерелами l можна визначити, якщо відомо заломлення скла біпризми n= 1, 5 та її кут заломлення 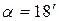 , відстань між щілиною і призмою d треба виміряти. Оскільки кути заломлення малі, можна з достатньою точністю рахувати, що S 1, S 2, S лежать в одній площині, яка перпендикулярна оптичній лаві. , відстань між щілиною і призмою d треба виміряти. Оскільки кути заломлення малі, можна з достатньою точністю рахувати, що S 1, S 2, S лежать в одній площині, яка перпендикулярна оптичній лаві.
З рис. 3 видно, що
так як кут Звідси
Відповідно
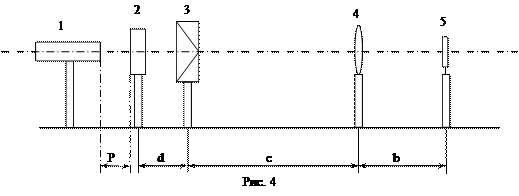
Для знаходження 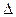 X та L на оптичній лаві (рис. 4) розміщують такі прилади: лазер 1, щільову діафрагму 2, біпризму 3, короткофокусну збиральну лінзу 4 і екран 5. Повзунки, в яких закріплені рейтери приладів, мають покажчики і можуть переміщуватися вздовж оптичної лави, на якій закріплена лінійка. Як джерело світла використовують лазер, який дає вузький монохроматичний пучок випромінювання. X та L на оптичній лаві (рис. 4) розміщують такі прилади: лазер 1, щільову діафрагму 2, біпризму 3, короткофокусну збиральну лінзу 4 і екран 5. Повзунки, в яких закріплені рейтери приладів, мають покажчики і можуть переміщуватися вздовж оптичної лави, на якій закріплена лінійка. Як джерело світла використовують лазер, який дає вузький монохроматичний пучок випромінювання.
З рисунка видно, що ширина інтерференційної лінії
Невідому відстань а можна знайти за допомогою формули для тонкої лінзи:
звідси
відповідно
З рис. 5 видно, що
Підставляючи вирази (12) і (13) у формулу (8), отримуємо кінцеву формулу
Знаючи показник заломлення скла біпризми n= 1, 5 та кут заломлення
|

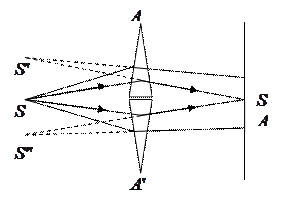 Біпризма Френеля являє собою дві призми з малим кутом заломлення
Біпризма Френеля являє собою дві призми з малим кутом заломлення 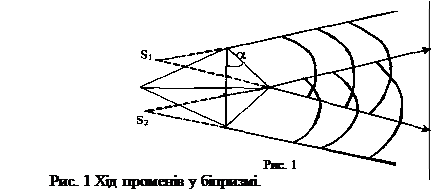
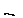
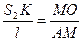
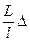 .
.
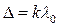 , де k = 0, ± 1, ± 2, то Х – координати максимумів (світлих ліній) визначаються з виразу (3):
, де k = 0, ± 1, ± 2, то Х – координати максимумів (світлих ліній) визначаються з виразу (3):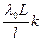
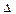 X = Xk+1 – Xk =
X = Xk+1 – Xk = 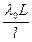
 X, відстань між уявними джерелами l і відстань від джерел до інтерференційної картини L, можна визначити довжину хвилі випромінювання у вакуумі
X, відстань між уявними джерелами l і відстань від джерел до інтерференційної картини L, можна визначити довжину хвилі випромінювання у вакуумі  :
: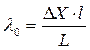
 »2d
»2d  – малий. Кут відхилення пов’язаний із кутом заломлення формулою
– малий. Кут відхилення пов’язаний із кутом заломлення формулою 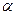 (див. Савельев И.В. Курс общей физики. – М.: Наука, 1966. Т.3, § 1).
(див. Савельев И.В. Курс общей физики. – М.: Наука, 1966. Т.3, § 1).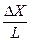
 Короткофокусну лінзу 4 (f = 35, 83 мм) використовують для отримання збільшеного зображення на екрані 5 інтерференційних ліній, які виникають в області між біпризмою 3 і лінзою (рис. 5).
Короткофокусну лінзу 4 (f = 35, 83 мм) використовують для отримання збільшеного зображення на екрані 5 інтерференційних ліній, які виникають в області між біпризмою 3 і лінзою (рис. 5). 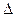 X¢ наступним чином:
X¢ наступним чином: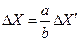 .
.
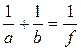 ,
,
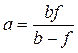 ,
,
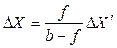 .
.
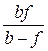 =
= 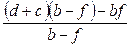 .
.
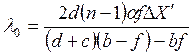
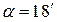 = 5, 24·10-3 рад, фокусну відстань лінзи f = 35, 83 мм та вимірюючи ширину інтерференційної лінії на екрані
= 5, 24·10-3 рад, фокусну відстань лінзи f = 35, 83 мм та вимірюючи ширину інтерференційної лінії на екрані 


