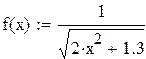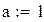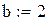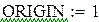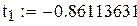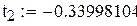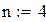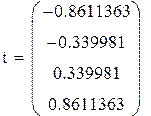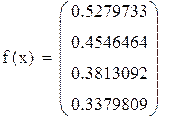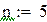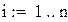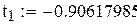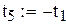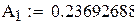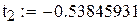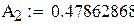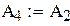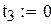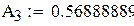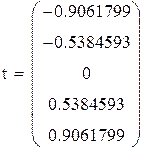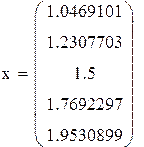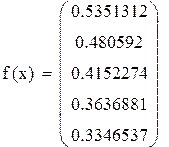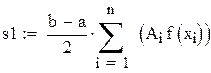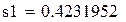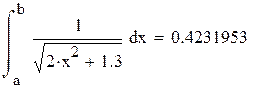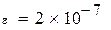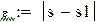Полиномы вида  называются полиномами Лежандра.
называются полиномами Лежандра.
Свойства этих полиномов:
1. 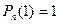 ,
, 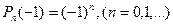 ;
;
2.  , где
, где  - любой полином степени k, меньшей n;
- любой полином степени k, меньшей n;
3. полином Лежандра  имеет n различных и действительных корней, которые расположены на интервале
имеет n различных и действительных корней, которые расположены на интервале 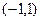 .
.
Первые пять полиномов Лежандра: 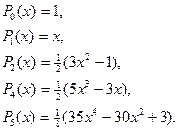
Рассмотрим функцию 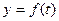 , заданную на стандартном промежутке
, заданную на стандартном промежутке  . Нужно подобрать точки
. Нужно подобрать точки  и коэффициенты
и коэффициенты  , чтобы квадратурная формула
, чтобы квадратурная формула
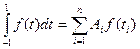 (8.14)
(8.14)
была точной для всех полиномов 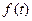 возможной наивысшей степени N. Так как в нашем распоряжении имеются 2n постоянных
возможной наивысшей степени N. Так как в нашем распоряжении имеются 2n постоянных 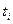 и
и  , а полином степени 2n-1 определяется 2n коэффициентами, то эта наивысшая степень полинома в общем случае равна N=2n-1.
, а полином степени 2n-1 определяется 2n коэффициентами, то эта наивысшая степень полинома в общем случае равна N=2n-1.
Для обеспечения равенства (8.14) необходимо и достаточно, чтобы оно было верным при 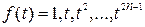 . Действительно, полагая
. Действительно, полагая 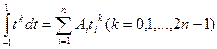 и
и 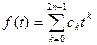 , будем иметь
, будем иметь 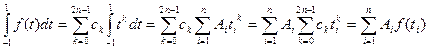 .
.
Таким образом, учитывая соотношения 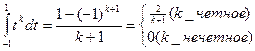 , заключаем, что для решения поставленной задачи достаточно определить постоянные
, заключаем, что для решения поставленной задачи достаточно определить постоянные 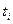 и
и 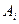 из системы 2n уравнений:
из системы 2n уравнений:
 (8.15)
(8.15)
Система (8.15) нелинейная, и ее решение обычным путем представляет большие трудности.
Рассмотрим полиномы 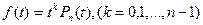 , где
, где 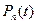 - полином Лежандра. Т.к. степени этих полиномов не превышают 2n-1, то на основании системы (8.15) для них должны быть справедлива формула (8.14) и
- полином Лежандра. Т.к. степени этих полиномов не превышают 2n-1, то на основании системы (8.15) для них должны быть справедлива формула (8.14) и  .
.
С другой стороны, в силу свойства ортогональности полиномов Лежандра выполнены неравенства:
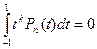 при
при 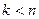 ,
,
поэтому
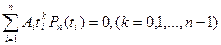 (8.16).
(8.16).
Равенства (8.16) будут обеспечены при любых значениях 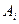 , если положить
, если положить 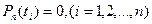 , т.е. для достижения наивысшей точности квадратурной формулы (8.14) в качестве точек
, т.е. для достижения наивысшей точности квадратурной формулы (8.14) в качестве точек 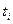 достаточно взять нули соответствующего полинома Лежандра. Как известно, из свойства 3, эти нули действительны, различны и расположены на интервале
достаточно взять нули соответствующего полинома Лежандра. Как известно, из свойства 3, эти нули действительны, различны и расположены на интервале 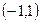 . Зная абсциссы
. Зная абсциссы 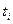 , легко можно найти из линейной системы первых n уравнений системы (8.15) коэффициенты Аi (i = 1, 2, …, n). Определитель этой подсистемы есть определитель Вандермонда
, легко можно найти из линейной системы первых n уравнений системы (8.15) коэффициенты Аi (i = 1, 2, …, n). Определитель этой подсистемы есть определитель Вандермонда
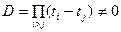
и, следовательно, 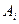 определяются однозначно.
определяются однозначно.
Формула (8.14), где 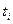 - нули полинома Лежандра
- нули полинома Лежандра 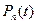 и
и  определяются из системы (8.15), называется квадратурной формулой Гаусса.
определяются из системы (8.15), называется квадратурной формулой Гаусса.
Рассмотрим теперь использование квадратурной формулы Гаусса для вычисления общего интеграла  . Делая замену переменной
. Делая замену переменной  , получим
, получим 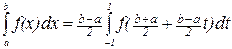 . Применяя к последнему интегралу, квадратурную формулу Гаусса получим:
. Применяя к последнему интегралу, квадратурную формулу Гаусса получим:
 , (8.16)
, (8.16)
где 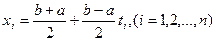 ,
, 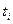 - нули полинома Лежандра
- нули полинома Лежандра 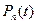 , т.е.
, т.е.  .
.
Остаточный член формулы Гаусса (8.16) с n узлами выражается следующим образом:
 .
.
Отсюда получаем:
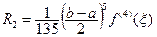 ,
,
 ,
,
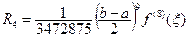 ,
,
 ,
,
 .
.
Выведем квадратурную формулу Гаусса для случая трех ординат. Полином Лежандра третьей степени есть
 .
.
Приравнивая этот полином нулю, находим:
 ,
,  ,
,  .
.
Для определения коэффициентов  в силу системы (8.15) имеем:
в силу системы (8.15) имеем:

Отсюда: 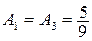 ,
, 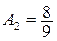 .
.
Следовательно, 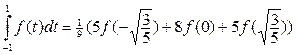 .
.
Таблица 8.2
Элементы формулы Гаусса
| n
| t
| ti
| Ai
|
|
|
|
|
|
|
| 1; 2
| ±0.57735027
|
|
|
| 1; 3
| ±0.77459667
| 0.55555556
0.88888889
|
|
| 4; 1
3; 2
| ±0.86113631
±0.33998104
| 0.34785484
0.65214516
|
|
| 5; 1
4; 2
| ±0.90617985
±0.53846931
| 0.23692688
0.47862868
0.56888889
|
|
| 6; 1
5; 2
4; 3
| ±0.93246951
±0.66120939
±0.23861919
| 0.17132450
0.36076158
0.46791394
|
|
| 7; 1
6; 2
5; 3
| ±0.94910791
±0.74153119
±0.40584515
| 0.12948496
0.27970540
0.38183006
0.41795918
|
Пример 8.4 Вычислить интеграл из примера 8.3. по формуле Гаусса для четырех и для пяти точек. Оценить точность вычислений.
В ответе сохраняем шесть верных знаков.
Ответ: 0, 423195
Рис. 8.4. Решение примера 8.3 в Mathcad

 называются полиномами Лежандра.
называются полиномами Лежандра.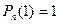 ,
, 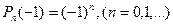 ;
; , где
, где  - любой полином степени k, меньшей n;
- любой полином степени k, меньшей n; имеет n различных и действительных корней, которые расположены на интервале
имеет n различных и действительных корней, которые расположены на интервале 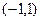 .
.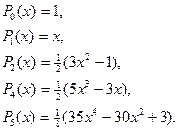
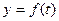 , заданную на стандартном промежутке
, заданную на стандартном промежутке  . Нужно подобрать точки
. Нужно подобрать точки  и коэффициенты
и коэффициенты  , чтобы квадратурная формула
, чтобы квадратурная формула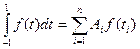 (8.14)
(8.14)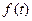 возможной наивысшей степени N. Так как в нашем распоряжении имеются 2n постоянных
возможной наивысшей степени N. Так как в нашем распоряжении имеются 2n постоянных 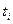 и
и 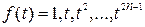 . Действительно, полагая
. Действительно, полагая 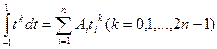 и
и 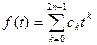 , будем иметь
, будем иметь 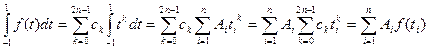 .
.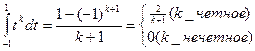 , заключаем, что для решения поставленной задачи достаточно определить постоянные
, заключаем, что для решения поставленной задачи достаточно определить постоянные 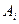 из системы 2n уравнений:
из системы 2n уравнений: (8.15)
(8.15)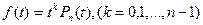 , где
, где 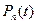 - полином Лежандра. Т.к. степени этих полиномов не превышают 2n-1, то на основании системы (8.15) для них должны быть справедлива формула (8.14) и
- полином Лежандра. Т.к. степени этих полиномов не превышают 2n-1, то на основании системы (8.15) для них должны быть справедлива формула (8.14) и  .
.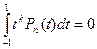 при
при 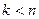 ,
,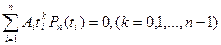 (8.16).
(8.16).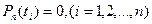 , т.е. для достижения наивысшей точности квадратурной формулы (8.14) в качестве точек
, т.е. для достижения наивысшей точности квадратурной формулы (8.14) в качестве точек 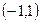 . Зная абсциссы
. Зная абсциссы 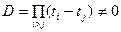
 . Делая замену переменной
. Делая замену переменной  , получим
, получим 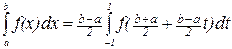 . Применяя к последнему интегралу, квадратурную формулу Гаусса получим:
. Применяя к последнему интегралу, квадратурную формулу Гаусса получим: , (8.16)
, (8.16)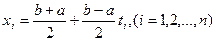 ,
,  .
. .
.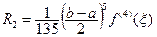 ,
, ,
,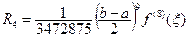 ,
, ,
, .
. .
. ,
,  ,
,  .
. в силу системы (8.15) имеем:
в силу системы (8.15) имеем:
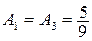 ,
, 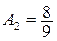 .
.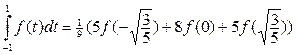 .
.