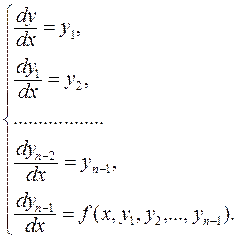Дифференциальных уравненийЗадача Коши для дифференциального уравнения n-го порядка:
заключается в отыскании функции
где Задача Коши для системы дифференциальных уравнений
заключается в отыскании функций
Систему, содержащую производные высших порядков и разрешенную относительно старших производных искомых функций, путем введения новых неизвестных функций можно привести в виду (9.2). В частности, дифференциальное уравнение n-го порядка
приводится к виду (9.1) с помощью замены переменных
что дает следующую систему
Если удается найти общее решение системы или уравнения, то задача Коши сводится к отысканию значений произвольных постоянных. Но найти общее решение задачи Коши удается в редких случаях, чаще приходится решать задачу приближенно. Приближенные методы в зависимости от формы, в которой они представляют решение, можно разделить на две группы. 1. Аналитические методы, дающие приближенное решение дифференциального уравнения в виде аналитического выражения. 2. Численные методы, дающие приближенное решение в виде таблицы. В дальнейшем будем считать, что для рассматриваемых уравнений выполнены условия существования и единственности решения.
|
(9.1)
, удовлетворяющей этому уравнению с начальными условиями: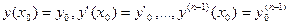
,
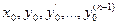- заданные числа.
(9.2)
, удовлетворяющих этой системе и начальным условиям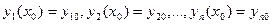
.
,
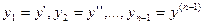