Метод последовательного дифференцирования
Рассмотрим уравнение
с начальными условиями
Начальные условия непосредственно дают нам значения
Значения Доказано, что если правая часть уравнения (9.1) в окрестности точки Аналогично применяется метод последовательного дифференцирования и для решения систем дифференциальных уравнений.
Пример 9.1 Найти первые семь членов разложения в степенной ряд решения уравнения y'' +0.1(y')2+(1+0.1 x) y = 0 с начальными условиями y (0)=1, y '(0)=2
Решение уравнения ищем в виде ряда
Непосредственно из начальных условий имеем y (0)=1, y '(0)=2 Разрешим уравнение относительно y'';
y' '=-0.1(y')2-(1+0.1 x)
используя начальные условия, получим
y'' (0)=-0.1·4-1·1=-1.4
Дифференцируем по x обе части уравнения последовательно получим: y''' =0.2 y' · y'' -0.1(xy' + y)- y' y'' '(0)=-1.54
y (4)=-0.2(y' y''' +(y'')2)-0.1(xy' '+2 y')- y'' y (4)(0)=1.224
y (5)= -0.2(y' · y (4)+3 y'' y''') -0.1(xy''' +3 y'')- y''' y (5)(0)=0.1768
y (6)(0)= -0.2(y' · y (5)+4 y'' y (4)+3(y''')2)-0.1(x y (4)+4 y''')- y (4) y (6)(0) =-0.7308
Искомое решение приближенно запишется в виде:
y (x)≈ 1+2 x -0.7 x 2-0.2567 x 3+0.051 x 4+0.00147 x 5-0.00101 x 6
Пример 9.2. Найти первые четыре члена разложения в степенной ряд решения y = y (x) z = z(x) системы с начальными условиями y (0)=1 z (0)=0
Функции y (x) и z (x) ищем в виде степенных рядов
при х =0 из уравнений системы следует, что y (0)'=1, z (0)'=0 Дифференцируем по х уравнения системы.
Находим y ''(0)=1, z ''(0)=1 Продифференцируем по х уравнения системы еще раз.
y ''' (0)=0, z''' (0)=3 Подставляя найденные значения производных в ряды, получим: y (x)≈ 1+ x -0.5 x 2, z (x)≈ 0.5 x 2-0.5 x 3
|

 (9.1)
(9.1)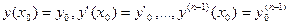 . Предположим, что искомое частное решение
. Предположим, что искомое частное решение  может быть разложено в ряд Тейлора по степеням разности
может быть разложено в ряд Тейлора по степеням разности 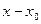 :
:
 при
при  . Значение
. Значение  найдем из уравнения (9.1), подставляя
найдем из уравнения (9.1), подставляя  и используя начальные условия:
и используя начальные условия: .
. последовательно определяются дифференцированием уравнения (9.1) и подстановкой
последовательно определяются дифференцированием уравнения (9.1) и подстановкой  при
при  .
. есть аналитическая функция своих аргументов, то при значениях x, достаточно близких к
есть аналитическая функция своих аргументов, то при значениях x, достаточно близких к  , существует единственное решение задачи Коши, которое разлагается в ряд Тейлора. Тогда частичная сумма этого ряда будет приближенным решением поставленной задачи.
, существует единственное решение задачи Коши, которое разлагается в ряд Тейлора. Тогда частичная сумма этого ряда будет приближенным решением поставленной задачи.








