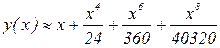Метод неопределенных коэффициентов
Этот метод рекомендуют применять при решении линейных дифференциальных уравнений с переменными коэффициентами. Суть метода покажем на примере уравнения второго порядка с начальными условиями
Решение данного уравнения будем искать в виде ряда
где Дифференцируем обе части равенства (9.3) два раза по x:
Подставляя полученные ряды для
Произведя умножение рядов и приравняв коэффициенты при одинаковых степенях x в левой и в правой частях тождества (9.4), получим систему
где Каждое уравнение системы (9.5) содержит на одно неизвестное больше по сравнению с предыдущим уравнением. Коэффициенты
Пример 9.4 Найти решение уравнения
Разложим коэффициенты уравнения в соответствующие степенные ряды. p (x)=- x q (x)=-1 Будем искать решение уравнения в виде ряда y=c0+c1x+c2x2+ c3x3+ c4x4+…+cnxn +… тогда
y'=c1+2c2x+3c3x2+4c4x3+…+n cnxn-1 +…
-y'x=-c1x-2c2x2-3c3x3-4c4x4-…- n cnxn +…
y''=2c2+6c3x+12c4x2+20c5x3+…+n(n-1) cnxn- 2+…
Подставив полученные ряды в уравнение примера, и приравняв коэффициенты при одинаковых степенях, получим систему для определения ci. c 0=0, c 1=1 возьмем из начальных условий.
x1 6 c3 = 0, x2 – c2 + 12 c4 = x3 – 2 c3 + 20 c5 = 0, x 4 – 3 c4 + 30 c6 = x 5 – 4 c5 + 42 c7 = 0, x 6 – 5 c6 + 56 c8 =
Решая последовательно систему, получим, что нечетные коэффициенты нули, а
Приближенное решение задачи получаем в виде
|

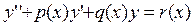
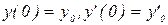 . Предположим, что каждый из коэффициентов уравнения можно разложить в ряд по степеням x:
. Предположим, что каждый из коэффициентов уравнения можно разложить в ряд по степеням x: ,
, 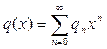 ,
, 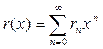 .
.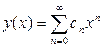 , (9.3)
, (9.3)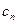 - коэффициенты, подлежащие определению.
- коэффициенты, подлежащие определению. ,
, 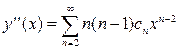 .
.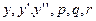 в уравнение
в уравнение 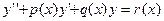 , получим:
, получим: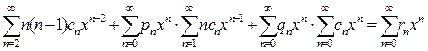 . (9.4)
. (9.4)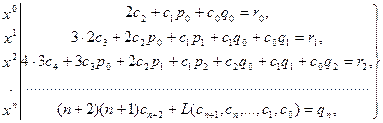 (9.5)
(9.5)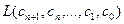 означает линейную функцию аргументов
означает линейную функцию аргументов 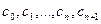 .
. определяются из начальных условий, а все остальные последовательно определяются из системы (9.5). Доказано, что если ряды
определяются из начальных условий, а все остальные последовательно определяются из системы (9.5). Доказано, что если ряды  ,
,  ,
,  сходятся при
сходятся при 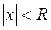 , то полученный степенной ряд сходится в той же области и является решением уравнения
, то полученный степенной ряд сходится в той же области и является решением уравнения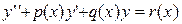 .
.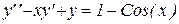 с начальными условиями
с начальными условиями 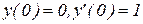 в виде степенного ряда. Ограничиться 6 членами ряда.
в виде степенного ряда. Ограничиться 6 членами ряда.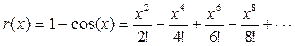
 x0 c0 + 2 c2 = 0,
x0 c0 + 2 c2 = 0, ,
,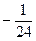 ,
,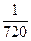 .
.