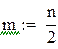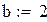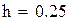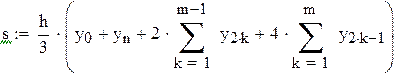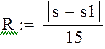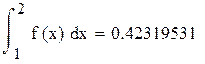Общая формула Симпсона и ее остаточный член
Пусть n=2m есть четное число и Следовательно, Отсюда получаем общую формулу Симпсона:
Введя обозначения
Если функция непрерывно дифференцируема до четвертого порядка, то ошибка формулы Симпсона на каждом удвоенном промежутке
Суммируя все эти ошибки, получим остаточный член общей формулы Симпсона в виде:
Следовательно
где Если задана предельная допустимая погрешность
Во многих случаях оценка погрешности квадратурной формулы весьма затруднительна. Тогда обычно применяют двойной пересчет с шагами h и 2 h и считают, что совпадающие десятичные знаки принадлежат точному значению интеграла. Предполагая, что на отрезке [ a, b ] производная
За приближенное значение интеграла целесообразно принять исправленное значение
Пример 8.2 Вычислить в Mathcad интеграл методом Симпсона для n=8. Оценить остаточный член.
Вычисляем для формулы Симпсона при n=4
Сделаем двойной пересчет при n=8
В качестве ответа возьмем
Остаточный член приблизительно равен
Это точный результат
Рис. 8.3. Решение примера 8.2 в Mathcad
|

 - значения функции
- значения функции  для равноотстоящих точек
для равноотстоящих точек 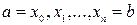 с шагом
с шагом  . Применяя формулу Симпсона к каждому удвоенному промежутку
. Применяя формулу Симпсона к каждому удвоенному промежутку  длины 2h, будем иметь
длины 2h, будем иметь  .
. .
. .
. , формулу можно записать в более простом виде:
, формулу можно записать в более простом виде: .
. дается формулой:
дается формулой: , где
, где  .
. .
. непрерывна на отрезке [ a, b ], поэтому найдется точка
непрерывна на отрезке [ a, b ], поэтому найдется точка  такая, что
такая, что  .
. , (8.9)
, (8.9) .
. , то, обозначив
, то, обозначив  , будем иметь для определения шага h неравенство:
, будем иметь для определения шага h неравенство: , отсюда
, отсюда  , т.е. h имеет порядок
, т.е. h имеет порядок  . Говорят, что степень точности метода Симпсона равна четырем
. Говорят, что степень точности метода Симпсона равна четырем меняется медленно, в силу формулы (8.9), получаем приближенное выражение для искомой ошибки
меняется медленно, в силу формулы (8.9), получаем приближенное выражение для искомой ошибки , где коэффициент M будем считать постоянным на промежутке интегрирования. Пусть
, где коэффициент M будем считать постоянным на промежутке интегрирования. Пусть  и
и  - приближенные значения интеграла
- приближенные значения интеграла 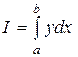 , полученные по формуле Симпсона соответственно с шагом h и H=2h. Имеем:
, полученные по формуле Симпсона соответственно с шагом h и H=2h. Имеем:  и
и  . Отсюда
. Отсюда .
. .
.