Метод выравнивания
К линейной функции можно привести любую функцию вида ψ (y)=aּ φ (x)+b, для этого достаточно сделать замену переменных, z=ψ (y), t=φ (x). Тогда мы получим z=aּ t+b. Рассмотрим показательную функцию Прологарифмируем это равенство. Получим ln(y)=ln(a)+x ln(b). Сделаем замену переменных z= ln(y), t=x и обозначим А= ln(b) B= ln(a). После замены получим z=A t+b. Аналогично делаются замены и для других функций из таблицы.
Таблица 7.1. Таблица замен
В таблице может не оказаться точек Для аналитических кривых существуют характерные точки, которые лежат на этих кривых. Например, если две точки принадлежат прямой, то и точка с координатами ( Остальные
Пример 7.1 Бомба «Рейда» это техническое устройство для изучения легкоиспаряющихся жидкостей. В эксперименте на бомбе «Рейда» при постоянной температуре измеряется манометром избыточное давление паров нефти при различных соотношениях объёмов газовой и жидкой фаз. Определить эмпирическую зависимость давления паров нефти от соотношения объёмов газовой и жидкой фаз методом наименьших квадратов. Набор экспериментальных данных представлен в таблицах
Для того, чтобы выбрать наиболее подходящую зависимость построим график по табличным данным
Можно предположить, что это будет: 1. показательная функция (строка 2 таблицы 7.1), 2. степенная функция (строка 5 таблицы 7.1), 3. дробно–рациональная функция (строка 3 таблицы 7.1). Выберем ту функцию, для которой
В таблице данных нет значений
Самые маленькие
Делаем замену переменных
После замены точки ложатся близко к прямой. Параметры этой прямой A и B
После замены z = At + B нашли A и B по методу наименьших квадратов, используя встроенные функции Mathcadа. Функция slope(x, y) возвращает значение углового коэффициента. Функция intercept(x, y) возвращает значение свободного параметра. Возвращаемся к исходной функции .
Из двух разных приближений одной и той же табличной функции лучшим считается то, для которого сумма квадратов отклонений меньше. Для этой же таблицы данных рассмотрим приближение, заданное показательной функцией
Для этой же таблицы данных рассмотрим приближение, заданное дробно-линейной функцией
Рис. 7.2. Решение примера 7.1 в Mathcad Лучшим приближением для этих экспериментальных данных будет степенная функция.
|

 .
.



























 ,
,  ,
,  .
. ,
,  ,
,  .
. - табличное значение для xар;
- табличное значение для xар; - табличное значение для хгеом;
- табличное значение для хгеом; - табличное значение для хгарм.
- табличное значение для хгарм. тогда точки
тогда точки  ,
,  доопределяют по соседним точкам таблицы с помощью линейной интерполяции.
доопределяют по соседним точкам таблицы с помощью линейной интерполяции. ,
,  ) принадлежит той же прямой, если две точки принадлежат гиперболе, то и точка (xар, yгарм) также принадлежат этой гиперболе. В таблице через
) принадлежит той же прямой, если две точки принадлежат гиперболе, то и точка (xар, yгарм) также принадлежат этой гиперболе. В таблице через  обозначено отклонение табличного значения
обозначено отклонение табличного значения  - отклонение табличного
- отклонение табличного  находятся аналогично, в зависимости от характерных точек. Функция, для которой
находятся аналогично, в зависимости от характерных точек. Функция, для которой  примет наименьшее значение и будет наиболее подходящей. После соответствующей замены переменных применяют метод наименьших квадратов.
примет наименьшее значение и будет наиболее подходящей. После соответствующей замены переменных применяют метод наименьших квадратов.


 ,
,  , подставляя
, подставляя  .
. ,
,  ,
,  , с помощью линейной интерполяции
, с помощью линейной интерполяции






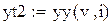




















 . Найдем методом выравнивания параметры для выбранных видов зависимостей. Будем искать аппроксимирующую функцию в виде
. Найдем методом выравнивания параметры для выбранных видов зависимостей. Будем искать аппроксимирующую функцию в виде .
.














 , строим её график и находим сумму квадратов отклонений от исходной таблицы значений. Можно также найти и среднеквадратичное отклонение.
, строим её график и находим сумму квадратов отклонений от исходной таблицы значений. Можно также найти и среднеквадратичное отклонение.
 .
.












 .
.






