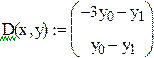Метод Рунге-Кутта для уравнений первого порядка
Рассмотрим задачу Коши для дифференциального уравнения.
с начальным условием Обозначим через
где
Для записи вычислений используется таблица Правило 4-го порядка точности.
Таблица 9.1. Шаблон для вычисления решения уравнения (9.6) по методу Рунге-Кутта.
Пример 9.6. Используя метод Рунге–Кутта составить таблицу приближенных значений интеграла дифференциального уравнения
Таблица 9.2. Решение примера методом Рунге-Кутта.
При решении задачи Коши для системы дифференциальных уравнений методом Рунге-Кутта
применим формулы
Для контроля правильности выбора шага h рекомендуется вычислять дробь Для определения точности пользуются двойным пересчетом.
где Для решения обыкновенных дифференциальных уравнений и систем в Mathcad предназначено несколько стандартных функций. В частности, для реализации метода Рунге-Кутта четвертого порядка существует функция rkfixed(y, a, b, n, D). Параметры этой функции: y -вектор начальных значений, а, b - начало и конец промежутка интегрирования, n -число интервалов, на которое делится промежуток интегрирования, D -вектор правых частей системы обыкновенных дифференциальных уравнений.
Применим данную функцию к решению примера 9.6.
Рис 9.2 Решение примера 9.5 в Mathcad
Пример 9.6. Решим систему обыкновенных дифференциальных уравнений первого порядка с помощью этой же стандартной функции на отрезке [0; 0.5] с шагом h=0.1
Рис 9.3. Решение примера 9.6 в Mathcad
Первый столбец таблицы это значения переменной x, второй столбец таблицы значения у, а третий столбец значения z в точках от ноля до 0, 5 с шагом 0, 1.
Пример 9.7. Решить задачу Коши для о.д.у. y " + 3y'-xy-x 3=5 y (0)=1 y' (0)=2 на отрезке [0; 0.5] с шагом h =0.1 Решение уравнения более высокого порядка находится сведением уравнения к системе уравнений первого порядка и применением стандартной функции маткада rkfixed. После замены переменных получаем систему
С начальными условиями y0(0)=1 y1(0)=2
Решение уравнения- второй столбец таблицы.
Рис 9.4. Решение примера 9.7 в Mathcad Список литературы
1. Демидович, Б.П. Основы вычислительной математики [Текст]: учеб. Пособие для студентов вузов/ Б.П. Демидович, И.А Марон. - Санкт-Петербург: Лань, 2009. - 672 с. 2. Копченова, Н. В. Вычислительная математика в примерах и задачах [Текст]: учеб. Пособие для студентов вузов/ Н. В. Копченова, И.А. Марон. - Санкт-Петербург: Лань, 2008. - 368 с. 3. Демидович, Б.П. Численные методы анализа. Приближение функций, дифференциальные и интегральные уравнения [Текст]: учеб. Пособие для студентов вузов/ Б.П. Демидович, И.А Марон, Э.З. Шувалова. - Санкт-Петербург: Лань, 2010. - 400 с. 4. Бахвалов, Н.С. Численные методы [Текст]: учеб. Пособие для студентов вузов/ Н.С. Бахвалов, Н.П., Жидков, Г.М. Кобельков. М: Бином, 2003. - 632 с. 5. Поршнев, С.В. Численные методы на базе Mathcad [Текст]: учеб. Пособие для студентов вузов/ С.В. Поршнев, И.В. Беленкова.- Санкт-Петербург: БХВ-Петербург, 2005. - 464 с. 6. Кирьянов, Д. В. MathCAD 14[Текст]: /Д.В. Кирьянов - Санкт-Петербург: БХВ-Петербург, 2007. - 704 с. Оглавление Введение. 3 Глава 1. Погрешность результата численного решения задачи. 5 1.1. Источники и классификация погрешностей. 5 1.2. Абсолютная и относительная погрешности. Формы записи данных. 6 1.3. Вычислительная погрешность. 9 Глава 2. Решение нелинейных уравнений. 11 2.1. Отделение корней уравнения. 11 2.1.1. Аналитический метод отделения корней. 11 2.1.2. Графический метод отделения корней. 12 2.2. Уточнение приближенных корней. 13 2.2.1. Метод половинного деления. 13 2.2.2 Метод хорд. 15 2.2.3. Метод Ньютона – метод касательных. 19 2.2.4. Модифицированный метод Ньютона. 21 2.2.5. Метод секущих. 21 2.2.6. Метод итераций. 22 Глава 3. Решения систем линейных алгебраических уравнений. 26 3.1. Метод итераций. 26 3.1.1. Оценка погрешности приближений процесса итераций. 28 3.1.2. Приведение линейной системы к виду, удобному для итерации: 29 3.2. Метод Зейделя. 31 3.3. Метод релаксаций. 33 Глава 4. Решение систем нелинейных уравнений. 36 4.1. Метод Ньютона для систем нелинейных уравнений. 36 4.2. Распространение метода Ньютона на системы из n уравнений с n неизвестными 39 4.3. Метод итераций для систем нелинейных уравнений. 41 4.4. Распространение метода итераций на системы из n уравнений с n неизвестными 44 Глава 5. Интерполяция. 46 5.1. Постановка задачи интерполирования. 46 5.2. Конечные разности. 47 5.3. Интерполяционная формула Ньютона №1. 48 5.4. Интерполяционная формула Ньютона №2. 49 5.5. Интерполяционный многочлен Лагранжа. 52 5.5.1. Вычисление лагранжевых коэффициентов. 53 5.5.2. Схема Эйткина. 56 5.5.3. Остаточный член формулы Лагранжа. 58 5.6. Обратное интерполирование. 58 5.6.1 Итерационные методы для обратного интерполирования. 59 Глава 6. Аппроксимация функций с помощью сплайнов. 61 6.1. Кубические сплайны.. 62 Глава 7. Методы обработки экспериментальных данных. 65 7.1 Построение эмпирической формулы. 65 7.2. Метод выбранных точек (метод натянутой нити) 65 7.3 Метод средних. 66 7.4. Метод наименьших квадратов. 66 7.5. Метод выравнивания. 68 7.6. Метод наименьших квадратов для полиномов. 76 Глава 8. Численное интегрирование. 81 8.1. Квадратурные формулы Ньютона-Котеса. 81 8.1. Формула трапеций и ее остаточный член. 82 8.2. Общая формула трапеций и ее остаточный член. 83 8.3 Формула Симпсона и ее остаточный член. 87 8.4. Общая формула Симпсона и ее остаточный член. 87 8.5. Формулы Ньютона-Котеса высших порядков. 91 8.6. Квадратурная формула Чебышева. 91 8.7. Квадратурная формула Гаусса. 94 Глава 9. Приближенное решение обыкновенных. 101 дифференциальных уравнений. 101 9.1. Аналитические методы.. 102 9.1.1. Метод последовательного дифференцирования. 102 9.1.2. Метод последовательных приближений. 104 9.1.3 Метод неопределенных коэффициентов. 105 9.2. Численные методы.. 107 9.2.1. Метод Эйлера. 107 9.2.2. Модифицированные методы Эйлера. 109 9.2.3. Метод Рунге-Кутта для уравнений первого порядка. 111 Список литературы.. 116
|


 .
. приближенное значение искомого решения в точке
приближенное значение искомого решения в точке  . По методу Рунге-Кутта вычисление приближенного значения
. По методу Рунге-Кутта вычисление приближенного значения  в следующей точке
в следующей точке 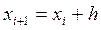 производится по формулам
производится по формулам

















 удовлетворяющего начальным условиям y(0)=0.2 на отрезке [0; 0.5] с шагом h=0.1. Все вычисления будем вести с четырьмя десятичными знаками, расположим их в таблице.
удовлетворяющего начальным условиям y(0)=0.2 на отрезке [0; 0.5] с шагом h=0.1. Все вычисления будем вести с четырьмя десятичными знаками, расположим их в таблице.





 . Величина q не должна превышать нескольких сотых. В противном случае шаг следует уменьшить.
. Величина q не должна превышать нескольких сотых. В противном случае шаг следует уменьшить. ,
, - точное решение уравнения (9.6) в точке
- точное решение уравнения (9.6) в точке  , а yn и
, а yn и 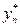 приближенные значения, полученные при расчете с шагом h и с шагом
приближенные значения, полученные при расчете с шагом h и с шагом  , соответственно. Если yn и
, соответственно. Если yn и 




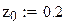

 с начальными условиями y(0)=2, z(0)=-1
с начальными условиями y(0)=2, z(0)=-1