1) Пусть  - момент k -го порядка,
- момент k -го порядка,  - центральный момент k -го порядка. Тогда верны оба равенства
- центральный момент k -го порядка. Тогда верны оба равенства
а)  ; б)
; б) 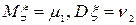 ;
;
в)  ; г)
; г)  .
.
2) Пусть  - центральный момент k -го порядка,
- центральный момент k -го порядка,  - центральный эмпирический момент k -го порядка, распределение генеральной совокупности
- центральный эмпирический момент k -го порядка, распределение генеральной совокупности  зависит от неизвестных параметров
зависит от неизвестных параметров  ,
,  - выборка. Тогда верны оба равенства
- выборка. Тогда верны оба равенства
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
3) Если генеральная совокупность  имеет распределение Пуассона с неизвестным параметром
имеет распределение Пуассона с неизвестным параметром  , то оценка
, то оценка  , найденная с помощью метода моментов, определяется равенством
, найденная с помощью метода моментов, определяется равенством
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
4) Если  , то уравнение правдоподобия выглядит так
, то уравнение правдоподобия выглядит так
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
5) Если 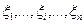 независимы, при всех
независимы, при всех 
 имеет распределение
имеет распределение 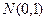 , то распределение
, то распределение  имеет случайная величина
имеет случайная величина
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
6) Какое свойство дисперсии используется в равенстве  ?
?
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 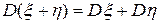 (для независимых
(для независимых  и
и  ).
).
7) Какое свойство математического ожидания используется в равенстве  ?
?
а) 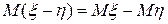 ; б)
; б)  ; в)
; в) 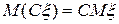 ; г)
; г)  .
.
8) Если  имеет распределение
имеет распределение  , то
, то  имеет распределение
имеет распределение
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
9) Если  имеет распределение
имеет распределение  , то
, то  имеет распределение
имеет распределение
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
10) Если  имеет распределение
имеет распределение  , то распределение
, то распределение  имеет случайная величина
имеет случайная величина
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
Ответы
| 1)
| 2)
| 3)
| 4)
| 5)
| 6)
| 7)
| 8)
| 9)
| 10)
|
| б
| б
| г
| г
| б
| а
| б
| а
| а
| б
|

 - момент k -го порядка,
- момент k -го порядка,  - центральный момент k -го порядка. Тогда верны оба равенства
- центральный момент k -го порядка. Тогда верны оба равенства ; б)
; б) 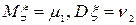 ;
; ; г)
; г)  .
. - центральный эмпирический момент k -го порядка, распределение генеральной совокупности
- центральный эмпирический момент k -го порядка, распределение генеральной совокупности  зависит от неизвестных параметров
зависит от неизвестных параметров  ,
,  - выборка. Тогда верны оба равенства
- выборка. Тогда верны оба равенства ;
; ;
; ;
; .
. , то оценка
, то оценка  , найденная с помощью метода моментов, определяется равенством
, найденная с помощью метода моментов, определяется равенством ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. , то уравнение правдоподобия выглядит так
, то уравнение правдоподобия выглядит так ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.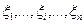 независимы, при всех
независимы, при всех 
 имеет распределение
имеет распределение 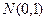 , то распределение
, то распределение  имеет случайная величина
имеет случайная величина ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. ?
? ; б)
; б)  ; в)
; в)  ; г)
; г) 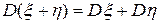 (для независимых
(для независимых  ).
). ?
?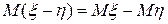 ; б)
; б)  ; в)
; в) 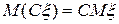 ; г)
; г)  .
. , то
, то  имеет распределение
имеет распределение ; б)
; б)  ; в)
; в)  ; г)
; г)  имеет распределение
имеет распределение ; б)
; б)  ; г)
; г)  .
. имеет случайная величина
имеет случайная величина ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.


