В данной теме будет рассмотрены распределения, которые не рассматривались ранее, но играют большую роль в математической статистике, в частности, при построении доверительных интервалов и проверке статистических гипотез.
Определение. Пусть случайные величины 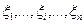 независимы и каждая из них имеет нормальное распределение с параметрами 0, 1 (обозначается
независимы и каждая из них имеет нормальное распределение с параметрами 0, 1 (обозначается 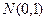 ), то есть при всех
), то есть при всех  выполняется равенство
выполняется равенство 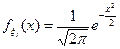 . Тогда говорят, что случайная величина
. Тогда говорят, что случайная величина 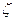 , определенная равенством
, определенная равенством 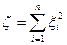 , имеет распределение
, имеет распределение  -квадрат с n степенями свободы (обозначается
-квадрат с n степенями свободы (обозначается  ).
).
Теорема. Если случайная величина 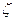 имеет распределение
имеет распределение  , то для ее характеристической функции выполняется равенство
, то для ее характеристической функции выполняется равенство 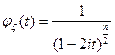 .
.
Эту теорему примем без доказательства.
Теорема (теорема сложения для распределения  ).
).
Пусть случайная величина  имеет распределение
имеет распределение  -квадрат с
-квадрат с  степенями свободы (
степенями свободы (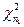 ), случайная величина
), случайная величина  имеет распределение
имеет распределение  -квадрат с
-квадрат с 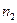 степенями свободы (
степенями свободы (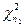 ),
),  и
и  независимы. Тогда сумма данных случайных величин
независимы. Тогда сумма данных случайных величин  +
+  имеет распределение
имеет распределение  -квадрат с числом степеней свободы
-квадрат с числом степеней свободы  (
(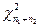 ).
).
Доказательство.
Поскольку случайная величина  имеет распределение
имеет распределение 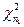 , то справедливо соотношение
, то справедливо соотношение 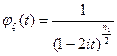 . Так как случайная величина
. Так как случайная величина  имеет распределение
имеет распределение 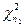 , то справедливо соотношение
, то справедливо соотношение 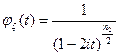 . Из независимости случайных величин
. Из независимости случайных величин  и
и  вытекает равенство
вытекает равенство 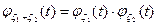 . Таким образом, получаем:
. Таким образом, получаем:
 .
.
Получили характеристическую функцию распределения 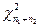 . Так как характеристическая функция полностью определяет распределение, то из полученного равенства вытекает, что случайная величина
. Так как характеристическая функция полностью определяет распределение, то из полученного равенства вытекает, что случайная величина  +
+  имеет распределение
имеет распределение  -квадрат с числом степеней свободы
-квадрат с числом степеней свободы  , что и требовалось доказать.
, что и требовалось доказать.
Определение. Пусть случайные величины  независимы, и каждая из них имеет нормальное распределение с параметрами 0, 1. Тогда говорят, что случайная величина
независимы, и каждая из них имеет нормальное распределение с параметрами 0, 1. Тогда говорят, что случайная величина 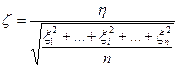 имеет распределение Стьюдента с n степенями свободы (
имеет распределение Стьюдента с n степенями свободы ( ).
).
Замечание. Исходя из определения распределения 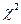 , распределение Стьюдента можно было определить следующим образом.
, распределение Стьюдента можно было определить следующим образом.
Определение 2. Пусть случайные величины  и
и 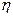 независимы,
независимы, 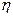 имеет нормальное распределение с параметрами 0, 1,
имеет нормальное распределение с параметрами 0, 1,  имеет распределение
имеет распределение  -квадрат с n степенями свободы. Тогда говорят, что случайная величина
-квадрат с n степенями свободы. Тогда говорят, что случайная величина 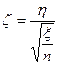 имеет распределение Стьюдента с n степенями свободы.
имеет распределение Стьюдента с n степенями свободы.
Замечание. И распределение  -квадрат, и распределение Стьюдента табулированы, поэтому в практических расчетах пользуются не формулами для их характеристических функций, плотностей и функций распределения, а таблицами.
-квадрат, и распределение Стьюдента табулированы, поэтому в практических расчетах пользуются не формулами для их характеристических функций, плотностей и функций распределения, а таблицами.

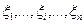 независимы и каждая из них имеет нормальное распределение с параметрами 0, 1 (обозначается
независимы и каждая из них имеет нормальное распределение с параметрами 0, 1 (обозначается 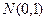 ), то есть при всех
), то есть при всех  выполняется равенство
выполняется равенство 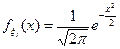 . Тогда говорят, что случайная величина
. Тогда говорят, что случайная величина 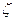 , определенная равенством
, определенная равенством 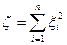 , имеет распределение
, имеет распределение  -квадрат с n степенями свободы (обозначается
-квадрат с n степенями свободы (обозначается  ).
).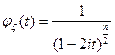 .
. имеет распределение
имеет распределение  степенями свободы (
степенями свободы (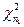 ), случайная величина
), случайная величина  имеет распределение
имеет распределение 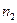 степенями свободы (
степенями свободы (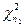 ),
),  (
(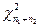 ).
).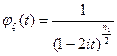 . Так как случайная величина
. Так как случайная величина 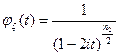 . Из независимости случайных величин
. Из независимости случайных величин 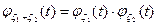 . Таким образом, получаем:
. Таким образом, получаем: .
. независимы, и каждая из них имеет нормальное распределение с параметрами 0, 1. Тогда говорят, что случайная величина
независимы, и каждая из них имеет нормальное распределение с параметрами 0, 1. Тогда говорят, что случайная величина 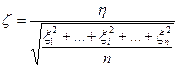 имеет распределение Стьюдента с n степенями свободы (
имеет распределение Стьюдента с n степенями свободы ( ).
).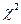 , распределение Стьюдента можно было определить следующим образом.
, распределение Стьюдента можно было определить следующим образом. и
и 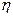 независимы,
независимы, 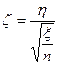 имеет распределение Стьюдента с n степенями свободы.
имеет распределение Стьюдента с n степенями свободы.


