Пусть у нас имеется гипотеза  о природе некоторого явления, которую мы по каким-то причинам выделяем и называем основной, противопоставляя ее множеству
о природе некоторого явления, которую мы по каким-то причинам выделяем и называем основной, противопоставляя ее множеству  альтернативных гипотез (
альтернативных гипотез ( может принимать значения 1, 2, … или вещественные значения, а в принципе пробегать любое множество).
может принимать значения 1, 2, … или вещественные значения, а в принципе пробегать любое множество).
Далее, имеется опыт, результат которого  есть элемент некоторого множества
есть элемент некоторого множества  , называемого выборочным пространством. Например, если опыт состоит в пересчете каких-то предметов, то
, называемого выборочным пространством. Например, если опыт состоит в пересчете каких-то предметов, то  - неотрицательное целое число, а
- неотрицательное целое число, а  . Если же опыт состоит в проведении какого-то измерения, то часто естественно считать, что его результат
. Если же опыт состоит в проведении какого-то измерения, то часто естественно считать, что его результат  может быть любым вещественным числом, а
может быть любым вещественным числом, а  - множество всех вещественных чисел. В случае нескольких измерений
- множество всех вещественных чисел. В случае нескольких измерений  - вектор, а
- вектор, а  - многомерное пространство.
- многомерное пространство.
Связь между гипотезами 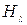 и результатом опыта
и результатом опыта  состоит в следующем. Предполагается, что в
состоит в следующем. Предполагается, что в  выделен достаточно широкий класс подмножеств
выделен достаточно широкий класс подмножеств  таких, что при любой верной гипотезе
таких, что при любой верной гипотезе 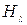 определены вероятности
определены вероятности  , т.е. вероятности того, что результат опыта
, т.е. вероятности того, что результат опыта  попадет в
попадет в  , если на самом деле верна гипотеза
, если на самом деле верна гипотеза 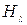 .
.
Формально процесс проверки гипотезы  состоит в том, что выбирается некоторое множество
состоит в том, что выбирается некоторое множество  (называемое критическим для гипотезы
(называемое критическим для гипотезы  ) и делается опыт. Если результат опыта
) и делается опыт. Если результат опыта  , то гипотеза
, то гипотеза  отвергается. Посмотрим, каким условиям должно удовлетворять
отвергается. Посмотрим, каким условиям должно удовлетворять  .
.
Хорошо было бы, если бы  (тогда бы мы никогда не отвергали верную гипотезу), а
(тогда бы мы никогда не отвергали верную гипотезу), а  при
при  (тогда мы всегда бы отвергали
(тогда мы всегда бы отвергали  , если на самом деле верна любая из гипотез
, если на самом деле верна любая из гипотез  ). Однако в практически интересных случаях, для того чтобы
). Однако в практически интересных случаях, для того чтобы  , множество
, множество  должно быть пустым. Но тогда и
должно быть пустым. Но тогда и 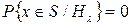 для любого
для любого  и вся процедура бесполезна.
и вся процедура бесполезна.
Поэтому исследователю приходится допускать ненулевые значения  . Единственное, что он может сделать, - выбрать заранее «уровень значимости», т.е. некоторое число
. Единственное, что он может сделать, - выбрать заранее «уровень значимости», т.е. некоторое число  , и потребовать, чтобы
, и потребовать, чтобы
 . (*)
. (*)
Если мы дорожим гипотезой  и не хотим ее отвергнуть понапрасну, то
и не хотим ее отвергнуть понапрасну, то  должно быть малым. Каким конкретно – довольно безразлично, поэтому можно уговориться выбирать одно из значений 0, 05; 0, 01 или 0, 001, как обычно и делается.
должно быть малым. Каким конкретно – довольно безразлично, поэтому можно уговориться выбирать одно из значений 0, 05; 0, 01 или 0, 001, как обычно и делается.
Итак, сначала назначается  , затем выбирается
, затем выбирается  , удовлетворяющее (*), и, наконец делается опыт. Очевидно, что
, удовлетворяющее (*), и, наконец делается опыт. Очевидно, что  (обозначаемая через
(обозначаемая через  ) есть вероятность напрасно отвергнуть
) есть вероятность напрасно отвергнуть  (когда она верна). Такая ошибка называется ошибкой первого рода. Из (*) следует, что вероятность ошибки первого рода не превосходит уровня значимости
(когда она верна). Такая ошибка называется ошибкой первого рода. Из (*) следует, что вероятность ошибки первого рода не превосходит уровня значимости  . Если
. Если  , где
, где  удовлетворяет (*), то говорят: «гипотеза
удовлетворяет (*), то говорят: «гипотеза  отвергается на уровне значимости
отвергается на уровне значимости  ».
».
Если  , то, казалось бы, следует сказать «гипотеза
, то, казалось бы, следует сказать «гипотеза  принимается». Но каждый статистик знает, что если гипотеза не отвергается одним способом, то, возможно, она будет отвергнута другим, и можно только сказать, что «гипотеза
принимается». Но каждый статистик знает, что если гипотеза не отвергается одним способом, то, возможно, она будет отвергнута другим, и можно только сказать, что «гипотеза  на уровне значимости
на уровне значимости  не отвергается».
не отвергается».
Кроме ошибки первого рода возможна еще ошибка второго рода, которая состоит в том, что гипотеза  не отвергается, когда на самом деле она не верна, а верна одна из гипотез
не отвергается, когда на самом деле она не верна, а верна одна из гипотез 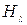 . Вероятность этой ошибки
. Вероятность этой ошибки  есть, очевидно,
есть, очевидно,
 .
.
Функция  , равная вероятности отвергнуть гипотезу
, равная вероятности отвергнуть гипотезу  , если на самом деле верна гипотеза
, если на самом деле верна гипотеза 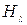 , называется функцией мощности статистического критерия
, называется функцией мощности статистического критерия  .
.
Пример. Пусть нам известно, что при выпечке сладких булочек по государственному стандарту полагается на 1000 булочек 10000 изюмин. Мы, однако, подозреваем, что изюм мог (по крайней мере, частично) разойтись по непредусмотренным законом каналам, и желаем это проверить. С этой целью мы покупаем одну булочку и пересчитываем в ней изюм. Если изюмин слишком мало, мы укрепляемся в своих подозрениях.
Попробуем формализовать эту процедуру с помощью только что введенных понятий.
Начнем с гипотез  и
и 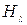 . Выберем параметр
. Выберем параметр  следующим образом:
следующим образом:  принимает значения на отрезке
принимает значения на отрезке  и обозначает долю украденного изюма. Гипотеза
и обозначает долю украденного изюма. Гипотеза  отвечает
отвечает  и означает, что ничего не украдено.
и означает, что ничего не украдено.
Опыт состоит в том, что мы пересчитываем изюмины в купленной булочке. Выборочное пространство  (множество всех возможных исходов опыта) состоит из чисел x =0, 1, 2, …, 10000, но нам удобнее считать его состоящим из всех чисел 0, 1, 2, … (считая, что значения
(множество всех возможных исходов опыта) состоит из чисел x =0, 1, 2, …, 10000, но нам удобнее считать его состоящим из всех чисел 0, 1, 2, … (считая, что значения  встречается с нулевой вероятностью).
встречается с нулевой вероятностью).
Вероятности 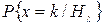 можно вычислить, применяя распределение Пуассона с параметром, равным среднему числу изюмин, приходящихся на одну булочку, т.е. при верной гипотезе
можно вычислить, применяя распределение Пуассона с параметром, равным среднему числу изюмин, приходящихся на одну булочку, т.е. при верной гипотезе 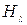 , пуассоновский параметр есть
, пуассоновский параметр есть  .
.
Таким образом, 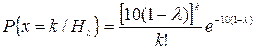 .
.
Перейдем к вопросу о выборе  . Вспомним, что
. Вспомним, что  ограничивает сверху вероятность ошибочно отвергнуть нулевую гипотезу, т.е., в нашем случае, ошибочно обвинить невинного человека. Поэтому приемлемо лишь значение
ограничивает сверху вероятность ошибочно отвергнуть нулевую гипотезу, т.е., в нашем случае, ошибочно обвинить невинного человека. Поэтому приемлемо лишь значение  , но в этом случае вся функция мощности будет равна 0, т.е. мы не сможем обвинить и виноватого. Эти соображения показывают, что статистические методы вряд ли пригодны для решения вопроса о возбуждении обвинения (тем более, для решения вопроса о виновности). Посмотрим, что же все-таки они могут дать. С этой целью испробуем два значения
, но в этом случае вся функция мощности будет равна 0, т.е. мы не сможем обвинить и виноватого. Эти соображения показывают, что статистические методы вряд ли пригодны для решения вопроса о возбуждении обвинения (тем более, для решения вопроса о виновности). Посмотрим, что же все-таки они могут дать. С этой целью испробуем два значения  :
:  и
и  .
.
Главный вопрос – как выбирать критическое множество  . Ясно, что хищение изюма проявится в том, что изюма в булочке будет слишком мало. Иными словами, критическое множество
. Ясно, что хищение изюма проявится в том, что изюма в булочке будет слишком мало. Иными словами, критическое множество  должно иметь вид
должно иметь вид  , где k следует выбирать из условия
, где k следует выбирать из условия  .
.
Задача о выборе k по заданному  очень легко решается с помощью таблиц распределения Пуассона. При
очень легко решается с помощью таблиц распределения Пуассона. При  имеем
имеем  , а при
, а при  имеем
имеем  . Функция мощности дается следующей таблицей:
. Функция мощности дается следующей таблицей:
| Параметр λ (доля украденного изюма)
| Функция мощности 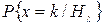 (вероятность возбуждения обвинения) (вероятность возбуждения обвинения)
|


| 

| 

|
| 0, 0
| 0, 010
| 0, 00050
| 0, 13
|
| 0, 1
| 0, 021
| 0, 0013
|
|
| 0, 2
| 0, 042
| 0, 0031
|
|
| 0, 3
| 0, 082
| 0, 0073
|
|
| 0, 4
| 0, 15
| 0, 017
|
|
| 0, 5
| 0, 27
| 0, 041
| 0, 76
|
| 0, 6
| 0, 43
| 0, 092
|
|
| 0, 7
| 0, 65
| 0, 2
|
|
| 0, 8
| 0, 86
| 0, 41
|
|
| 0, 9
| 0, 98
| 0, 74
|
|
| 1, 0
|
|
|
|
Из таблицы видно, в частности, что если вероятность ложного обвинения ограничить сверху числом 0, 001, то она на самом деле буде равна 0, 00050. При этом того, кто украл половину изюма ( ), мы обвиним с вероятностью 0, 041.
), мы обвиним с вероятностью 0, 041.
Нельзя ли все же извлечь из статистики некоторую пользу? Договоримся решать вопрос об обвинении не при помощи статистики, а при помощи прямого наблюдения. Но в таком случае, если допустить, что 80% всех работников честны и лишь 20% нечестны, то 80% рабочего времени «наблюдателя» будет потеряно впустую. Будем теперь проверять нашу гипотезу  на совершенно ином уровне значимости
на совершенно ином уровне значимости  , договорившись, что отбрасывание гипотезы не означает возбуждение обвинения, а лишь установление в соответствующем месте наблюдения. Как видно из таблицы, вероятность ошибки первого рода, т.е. напрасной посылки «наблюдателя» есть 0, 13 и, таким образом, лишь 0, 13·0, 80=10, 4% рабочего времени «наблюдателя» будет потеряно впустую. С другой стороны, если
, договорившись, что отбрасывание гипотезы не означает возбуждение обвинения, а лишь установление в соответствующем месте наблюдения. Как видно из таблицы, вероятность ошибки первого рода, т.е. напрасной посылки «наблюдателя» есть 0, 13 и, таким образом, лишь 0, 13·0, 80=10, 4% рабочего времени «наблюдателя» будет потеряно впустую. С другой стороны, если  , то вероятность посылки наблюдателя и тем самым обнаружения хищения (при его обнаружении в следующий раз) равна 0, 76, что вполне удовлетворительно.
, то вероятность посылки наблюдателя и тем самым обнаружения хищения (при его обнаружении в следующий раз) равна 0, 76, что вполне удовлетворительно.
Рассмотренное положение вообще характерно для применения статистических методов: не решая до конца научной или технической задачи, они позволяют ценой сравнительно небольших расходов наметить объект или план углубленного научного исследования. Таким образом, мы убедились в справедливости афоризма «статистике часто принадлежит первое слово, но никогда последнее».
Для проверки гипотез существуют различные критерии. Рассмотрим наиболее употребительные из них.
Критерий знаков. Рассмотрим следующую ситуацию. Пусть на предприятии измерили значения некоторых экономических критериев и получили следующую выборку: X=(9, 11, 10, 8, 15, 13, 10, 12, 14, 9) (числа совершенно условные). Затем внедрили некоторое новшество и через какое-то время, опять измерили те же показатели, получив выборку Y=(11, 12, 11, 10, 17, 15, 11, 15, 17, 11). Возникает вопрос: подействовало новшество или нет. С точки зрения математической статистики необходимо выяснить, являются ли генеральные совокупности  и
и  , из которых получены данные выборки X и Y однородными, то есть, выполняется ли равенство
, из которых получены данные выборки X и Y однородными, то есть, выполняется ли равенство  ? В нашем случае, скорее всего,
? В нашем случае, скорее всего,  и
и  не однородны, то есть новшество подействовало. Действительно, если обозначить
не однородны, то есть новшество подействовало. Действительно, если обозначить  ,
,  , то видно, что в нашем примере выполняется условие
, то видно, что в нашем примере выполняется условие 
 . Конечно, это может быть случайностью. Но при верной гипотезе
. Конечно, это может быть случайностью. Но при верной гипотезе  (
( ) справедливо равенство
) справедливо равенство  (считаем, что равенство
(считаем, что равенство 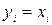 невозможно). Поэтому вероятность того, что все 10 разностей
невозможно). Поэтому вероятность того, что все 10 разностей  положительны (при однородности выборок) в нашем примере равна
положительны (при однородности выборок) в нашем примере равна  . Таким образом, если мы отвергаем гипотезу
. Таким образом, если мы отвергаем гипотезу  и посчитаем что выборки неоднородны, то есть новшество подействовало, то вероятность ошибки первого рода будет равна
и посчитаем что выборки неоднородны, то есть новшество подействовало, то вероятность ошибки первого рода будет равна  , что вполне допустимо.
, что вполне допустимо.
Теперь рассмотрим критерий знаков подробнее. Пусть  и
и  - две генеральные совокупности. Основная гипотеза
- две генеральные совокупности. Основная гипотеза  состоит в том, что
состоит в том, что  (совокупности однородны). Альтернативная гипотеза
(совокупности однородны). Альтернативная гипотеза  состоит в том, что
состоит в том, что  (совокупности неоднородны). Для проверки данной гипотезы проводят эксперимент, в результате которого получают выборку
(совокупности неоднородны). Для проверки данной гипотезы проводят эксперимент, в результате которого получают выборку  объема n из первой генеральной совокупности и выборку того же объема
объема n из первой генеральной совокупности и выборку того же объема  из второй генеральной совокупности. На их основе строится выборка
из второй генеральной совокупности. На их основе строится выборка  , где при всех
, где при всех 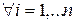
 . Считаем, что равенство
. Считаем, что равенство 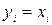 невозможно (этого можно добиться увеличением точности измерений или исключением нулевых разностей). Тогда при верной гипотезе
невозможно (этого можно добиться увеличением точности измерений или исключением нулевых разностей). Тогда при верной гипотезе  справедливо равенство
справедливо равенство  . Пусть
. Пусть  - количество положительных разностей. При верной гипотезе
- количество положительных разностей. При верной гипотезе 
 имеет распределение Бернулли с параметрами
имеет распределение Бернулли с параметрами  . Следовательно, при всех
. Следовательно, при всех  выполняется равенство
выполняется равенство  , и при
, и при  справедливы соотношения
справедливы соотношения 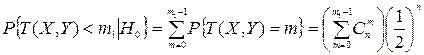 ,
,
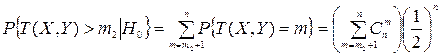 .
.
Следовательно, для любого уровня значимости  и объема выборки n можно найти (по таблицам распределения Бернулли) такие числа
и объема выборки n можно найти (по таблицам распределения Бернулли) такие числа  и
и 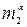 , для которых выполняются неравенства
, для которых выполняются неравенства  ,
,  . (**)
. (**)
Тогда будет справедливо соотношение  .
.
Таким образом, проверка гипотезы об однородности двух генеральных совокупностей с помощью критерия знаков производится следующим образом. Назначается уровень значимости  , и находятся числа
, и находятся числа  и
и 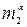 , удовлетворяющие условиям (**). В результате эксперимента получают выборки X, Y и вычисляют
, удовлетворяющие условиям (**). В результате эксперимента получают выборки X, Y и вычисляют  . Если выполняется одно из неравенств
. Если выполняется одно из неравенств  или
или 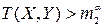 , то гипотеза
, то гипотеза  отвергается на уровне значимости
отвергается на уровне значимости  . Если же справедливо неравенство
. Если же справедливо неравенство 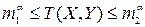 , то гипотеза
, то гипотеза  не отвергается на уровне значимости
не отвергается на уровне значимости  (но может быть отвергнута на некотором другом уровне значимости).
(но может быть отвергнута на некотором другом уровне значимости).
Замечание. Таким образом, гипотеза об однородности отвергается, если положительных разностей или слишком много, или слишком мало. Например, при 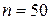 верны равенства
верны равенства 
 .
.

 о природе некоторого явления, которую мы по каким-то причинам выделяем и называем основной, противопоставляя ее множеству
о природе некоторого явления, которую мы по каким-то причинам выделяем и называем основной, противопоставляя ее множеству  альтернативных гипотез (
альтернативных гипотез ( может принимать значения 1, 2, … или вещественные значения, а в принципе пробегать любое множество).
может принимать значения 1, 2, … или вещественные значения, а в принципе пробегать любое множество). есть элемент некоторого множества
есть элемент некоторого множества  , называемого выборочным пространством. Например, если опыт состоит в пересчете каких-то предметов, то
, называемого выборочным пространством. Например, если опыт состоит в пересчете каких-то предметов, то  . Если же опыт состоит в проведении какого-то измерения, то часто естественно считать, что его результат
. Если же опыт состоит в проведении какого-то измерения, то часто естественно считать, что его результат 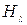 и результатом опыта
и результатом опыта  таких, что при любой верной гипотезе
таких, что при любой верной гипотезе  , т.е. вероятности того, что результат опыта
, т.е. вероятности того, что результат опыта  , если на самом деле верна гипотеза
, если на самом деле верна гипотеза  (называемое критическим для гипотезы
(называемое критическим для гипотезы  , то гипотеза
, то гипотеза  (тогда бы мы никогда не отвергали верную гипотезу), а
(тогда бы мы никогда не отвергали верную гипотезу), а  при
при  (тогда мы всегда бы отвергали
(тогда мы всегда бы отвергали  ). Однако в практически интересных случаях, для того чтобы
). Однако в практически интересных случаях, для того чтобы 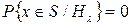 для любого
для любого  . Единственное, что он может сделать, - выбрать заранее «уровень значимости», т.е. некоторое число
. Единственное, что он может сделать, - выбрать заранее «уровень значимости», т.е. некоторое число  , и потребовать, чтобы
, и потребовать, чтобы . (*)
. (*) должно быть малым. Каким конкретно – довольно безразлично, поэтому можно уговориться выбирать одно из значений 0, 05; 0, 01 или 0, 001, как обычно и делается.
должно быть малым. Каким конкретно – довольно безразлично, поэтому можно уговориться выбирать одно из значений 0, 05; 0, 01 или 0, 001, как обычно и делается. ) есть вероятность напрасно отвергнуть
) есть вероятность напрасно отвергнуть  есть, очевидно,
есть, очевидно, .
. , равная вероятности отвергнуть гипотезу
, равная вероятности отвергнуть гипотезу  и обозначает долю украденного изюма. Гипотеза
и обозначает долю украденного изюма. Гипотеза  и означает, что ничего не украдено.
и означает, что ничего не украдено. встречается с нулевой вероятностью).
встречается с нулевой вероятностью).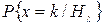 можно вычислить, применяя распределение Пуассона с параметром, равным среднему числу изюмин, приходящихся на одну булочку, т.е. при верной гипотезе
можно вычислить, применяя распределение Пуассона с параметром, равным среднему числу изюмин, приходящихся на одну булочку, т.е. при верной гипотезе  .
.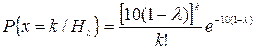 .
. , но в этом случае вся функция мощности будет равна 0, т.е. мы не сможем обвинить и виноватого. Эти соображения показывают, что статистические методы вряд ли пригодны для решения вопроса о возбуждении обвинения (тем более, для решения вопроса о виновности). Посмотрим, что же все-таки они могут дать. С этой целью испробуем два значения
, но в этом случае вся функция мощности будет равна 0, т.е. мы не сможем обвинить и виноватого. Эти соображения показывают, что статистические методы вряд ли пригодны для решения вопроса о возбуждении обвинения (тем более, для решения вопроса о виновности). Посмотрим, что же все-таки они могут дать. С этой целью испробуем два значения  и
и  .
. , где k следует выбирать из условия
, где k следует выбирать из условия  .
. , а при
, а при  имеем
имеем  . Функция мощности дается следующей таблицей:
. Функция мощности дается следующей таблицей:

 ), мы обвиним с вероятностью 0, 041.
), мы обвиним с вероятностью 0, 041. и
и  , из которых получены данные выборки X и Y однородными, то есть, выполняется ли равенство
, из которых получены данные выборки X и Y однородными, то есть, выполняется ли равенство  ? В нашем случае, скорее всего,
? В нашем случае, скорее всего,  ,
,  , то видно, что в нашем примере выполняется условие
, то видно, что в нашем примере выполняется условие 
 . Конечно, это может быть случайностью. Но при верной гипотезе
. Конечно, это может быть случайностью. Но при верной гипотезе  (считаем, что равенство
(считаем, что равенство 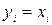 невозможно). Поэтому вероятность того, что все 10 разностей
невозможно). Поэтому вероятность того, что все 10 разностей  положительны (при однородности выборок) в нашем примере равна
положительны (при однородности выборок) в нашем примере равна  . Таким образом, если мы отвергаем гипотезу
. Таким образом, если мы отвергаем гипотезу  , что вполне допустимо.
, что вполне допустимо. состоит в том, что
состоит в том, что  (совокупности неоднородны). Для проверки данной гипотезы проводят эксперимент, в результате которого получают выборку
(совокупности неоднородны). Для проверки данной гипотезы проводят эксперимент, в результате которого получают выборку  , где при всех
, где при всех 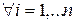
 . Считаем, что равенство
. Считаем, что равенство  . Пусть
. Пусть  - количество положительных разностей. При верной гипотезе
- количество положительных разностей. При верной гипотезе  . Следовательно, при всех
. Следовательно, при всех  выполняется равенство
выполняется равенство  , и при
, и при  справедливы соотношения
справедливы соотношения 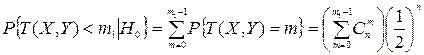 ,
,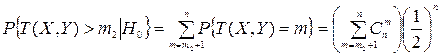 .
. и
и 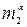 , для которых выполняются неравенства
, для которых выполняются неравенства  ,
,  . (**)
. (**) .
. или
или 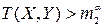 , то гипотеза
, то гипотеза 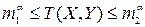 , то гипотеза
, то гипотеза 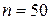 верны равенства
верны равенства 
 .
.


