Мы рассмотрим два основных метода нахождения оценок параметров – метод моментов и метод наибольшего правдоподобия. Перед рассмотрением метода моментов необходимо дать определения моментов и эмпирических моментов.
Определение. Пусть  - случайная величина,
- случайная величина,  . Момент k - го порядка случайной величины
. Момент k - го порядка случайной величины  обозначается
обозначается  и определяется равенством
и определяется равенством  . Центральный момент k - го порядка случайной величины
. Центральный момент k - го порядка случайной величины  обозначается
обозначается  и определяется равенством
и определяется равенством  . Абсолютный момент k - го порядка обозначается
. Абсолютный момент k - го порядка обозначается  и определяется равенством
и определяется равенством 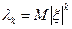 .
.
Замечание. Математическое ожидание случайной величины является ее моментом первого порядка, а дисперсия – центральным моментом второго порядка.
Замечание. Если распределение случайной величины  зависит от параметров
зависит от параметров  , то ее моменты являются функциями от этих параметров. Например, пусть случайная величина
, то ее моменты являются функциями от этих параметров. Например, пусть случайная величина  имеет распределение Пуассона с параметром
имеет распределение Пуассона с параметром 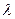 , то есть при любом
, то есть при любом  верно соотношение
верно соотношение  . Тогда выполняются равенства
. Тогда выполняются равенства  ,
,  . Если же случайная величина
. Если же случайная величина  имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами  , то есть ее плотность распределения задается равенством
, то есть ее плотность распределения задается равенством  , то верны равенства
, то верны равенства 
 .
.
Определение. Пусть дана выборка  ,
,  . Эмпирический момент k - го порядка обозначается
. Эмпирический момент k - го порядка обозначается 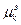 и определяется равенством
и определяется равенством  . Центральный эмпирический момент k - го порядка обозначается
. Центральный эмпирический момент k - го порядка обозначается  и определяется равенством
и определяется равенством  . Абсолютный эмпирический момент k - го порядка обозначается
. Абсолютный эмпирический момент k - го порядка обозначается  и определяется равенством
и определяется равенством  .
.
Замечание. Эмпирическое среднее  является эмпирическим моментом первого порядка, а эмпирическая дисперсия
является эмпирическим моментом первого порядка, а эмпирическая дисперсия  - центральным эмпирическим моментом второго порядка.
- центральным эмпирическим моментом второго порядка.
Замечание. Эмпирические моменты являются функциями от выборки.
Метод моментов, нахождения оценок параметров распределения, состоит в следующем. Пусть распределение генеральной совокупности  зависит от l независимых параметров
зависит от l независимых параметров  . Вычисляются l моментов, являющихся функциями данных параметров (например
. Вычисляются l моментов, являющихся функциями данных параметров (например  ) и l одноименных эмпирических моментов, являющихся функциями выборки (например
) и l одноименных эмпирических моментов, являющихся функциями выборки (например  ). Затем составляется и решается следующая система из l уравнений и l неизвестными:
). Затем составляется и решается следующая система из l уравнений и l неизвестными:  ,
,  .
.
Решения данной системы  ,
,  и являются оценками параметров
и являются оценками параметров  , найденными с помощью метода моментов.
, найденными с помощью метода моментов.
Пример 1. Пусть генеральная совокупность  имеет распределение Бернулли с известным числом опытов N и неизвестной вероятностью успеха в одном опыте
имеет распределение Бернулли с известным числом опытов N и неизвестной вероятностью успеха в одном опыте  . Для оценки неизвестного параметра
. Для оценки неизвестного параметра  воспользуемся методом моментов. Поскольку неизвестный параметр один, то нужно решить уравнение
воспользуемся методом моментов. Поскольку неизвестный параметр один, то нужно решить уравнение  , то есть
, то есть  . Но
. Но  . Таким образом, получаем:
. Таким образом, получаем:  , откуда
, откуда  .
.
При использовании метода наибольшего правдоподобия оценка 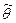 неизвестного параметра
неизвестного параметра  находится из условия
находится из условия  , где
, где  - функция правдоподобия.
- функция правдоподобия.
Поскольку функции  и
и  достигают максимума в одной точке, то из технических соображений удобнее максимизировать по
достигают максимума в одной точке, то из технических соображений удобнее максимизировать по  не
не  , а
, а  . Если функция
. Если функция  дифференцируема по параметру
дифференцируема по параметру  , то оценку наибольшего правдоподобия можно находить из уравнения
, то оценку наибольшего правдоподобия можно находить из уравнения 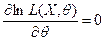 , называемого уравнением правдоподобия. При этом нужно убедиться в том, что найдена точка максимума, а не минимума, данной функции, проверив, например, выполнения условия
, называемого уравнением правдоподобия. При этом нужно убедиться в том, что найдена точка максимума, а не минимума, данной функции, проверив, например, выполнения условия  .
.
Пример 2. Пусть генеральная совокупность  имеет распределение Пуассона с неизвестным параметром
имеет распределение Пуассона с неизвестным параметром  , то есть при всех
, то есть при всех  верно равенство
верно равенство  . Тогда имеем:
. Тогда имеем:
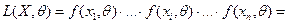
 ,
,
 ,
,
 .
.
Составляя уравнение правдоподобия, получаем:
 , откуда получаем
, откуда получаем  .
.
Поскольку 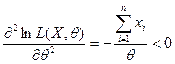 , то найденная оценка максимизирует функцию правдоподобия.
, то найденная оценка максимизирует функцию правдоподобия.
Пример 3. Пусть генеральная совокупность  имеет показательное распределение с параметром
имеет показательное распределение с параметром  , то есть
, то есть  при
при  . Получаем
. Получаем
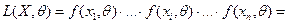
 ,
,
 ,
,  .
.
Из уравнения правдоподобия имеем  , откуда получаем
, откуда получаем  . Поскольку
. Поскольку  , то найденная оценка максимизирует функцию правдоподобия.
, то найденная оценка максимизирует функцию правдоподобия.

 - случайная величина,
- случайная величина,  . Момент k - го порядка случайной величины
. Момент k - го порядка случайной величины  и определяется равенством
и определяется равенством  . Центральный момент k - го порядка случайной величины
. Центральный момент k - го порядка случайной величины  и определяется равенством
и определяется равенством  . Абсолютный момент k - го порядка обозначается
. Абсолютный момент k - го порядка обозначается  и определяется равенством
и определяется равенством 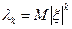 .
. , то ее моменты являются функциями от этих параметров. Например, пусть случайная величина
, то ее моменты являются функциями от этих параметров. Например, пусть случайная величина 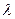 , то есть при любом
, то есть при любом  верно соотношение
верно соотношение  . Тогда выполняются равенства
. Тогда выполняются равенства  ,
,  . Если же случайная величина
. Если же случайная величина  , то есть ее плотность распределения задается равенством
, то есть ее плотность распределения задается равенством  , то верны равенства
, то верны равенства 
 .
. ,
, 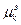 и определяется равенством
и определяется равенством  . Центральный эмпирический момент k - го порядка обозначается
. Центральный эмпирический момент k - го порядка обозначается  и определяется равенством
и определяется равенством  . Абсолютный эмпирический момент k - го порядка обозначается
. Абсолютный эмпирический момент k - го порядка обозначается  и определяется равенством
и определяется равенством  .
. является эмпирическим моментом первого порядка, а эмпирическая дисперсия
является эмпирическим моментом первого порядка, а эмпирическая дисперсия  - центральным эмпирическим моментом второго порядка.
- центральным эмпирическим моментом второго порядка. ) и l одноименных эмпирических моментов, являющихся функциями выборки (например
) и l одноименных эмпирических моментов, являющихся функциями выборки (например  ). Затем составляется и решается следующая система из l уравнений и l неизвестными:
). Затем составляется и решается следующая система из l уравнений и l неизвестными:  ,
,  .
. ,
,  и являются оценками параметров
и являются оценками параметров  . Для оценки неизвестного параметра
. Для оценки неизвестного параметра  , то есть
, то есть  . Но
. Но  . Таким образом, получаем:
. Таким образом, получаем:  , откуда
, откуда  .
.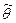 неизвестного параметра
неизвестного параметра  , где
, где  - функция правдоподобия.
- функция правдоподобия. достигают максимума в одной точке, то из технических соображений удобнее максимизировать по
достигают максимума в одной точке, то из технических соображений удобнее максимизировать по 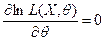 , называемого уравнением правдоподобия. При этом нужно убедиться в том, что найдена точка максимума, а не минимума, данной функции, проверив, например, выполнения условия
, называемого уравнением правдоподобия. При этом нужно убедиться в том, что найдена точка максимума, а не минимума, данной функции, проверив, например, выполнения условия  .
. верно равенство
верно равенство  . Тогда имеем:
. Тогда имеем: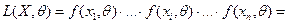
 ,
, ,
, .
. , откуда получаем
, откуда получаем  .
.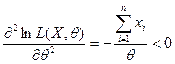 , то найденная оценка максимизирует функцию правдоподобия.
, то найденная оценка максимизирует функцию правдоподобия. при
при  . Получаем
. Получаем ,
, ,
,  .
. , откуда получаем
, откуда получаем  . Поскольку
. Поскольку  , то найденная оценка максимизирует функцию правдоподобия.
, то найденная оценка максимизирует функцию правдоподобия.


