Для характеристики отклонения оценки от оцениваемого параметра вводится следующая величина.
Определение. Пусть  - оценка параметра
- оценка параметра  . Вариация данной оценки обозначается
. Вариация данной оценки обозначается  и определяется равенством
и определяется равенством  .
.
Теорема. Вариация несмещенной оценки совпадает с ее дисперсией.
Доказательство.
Пусть  - несмещенная оценка параметра
- несмещенная оценка параметра  . Следовательно, выполняется равенство
. Следовательно, выполняется равенство  . Имеем:
. Имеем:  , что и требовалось доказать.
, что и требовалось доказать.
Ясно, что чем меньше вариация оценки, тем лучше она оценивает данный параметр. Оказывается, существует нижний предел вариации оценки. Прежде чем доказать соответствующее утверждение, дадим необходимые определения.
Определение. Пусть распределение генеральной совокупности  зависит от неизвестного параметра
зависит от неизвестного параметра  ,
, 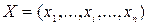 - выборка.
- выборка.
Тогда функция правдоподобия обозначается  и определяется равенством
и определяется равенством  , где
, где  , если генеральная совокупность
, если генеральная совокупность  имеет дискретное распределение, и
имеет дискретное распределение, и  , если
, если  имеет абсолютно-непрерывное распределение с плотностью
имеет абсолютно-непрерывное распределение с плотностью  .
.
Теорема. Пусть  - несмещенная оценка параметра
- несмещенная оценка параметра  , и функция правдоподобия
, и функция правдоподобия  дифференцируема по параметру
дифференцируема по параметру  . Тогда справедливо неравенство
. Тогда справедливо неравенство  , называемое неравенством Рао-Крамера.
, называемое неравенством Рао-Крамера.
Доказательство.
Доказательство проведем для случая, когда генеральная совокупность  имеет абсолютно-непрерывное распределение с плотностью
имеет абсолютно-непрерывное распределение с плотностью  . Тогда функция правдоподобия
. Тогда функция правдоподобия  является плотностью распределения случайного вектора
является плотностью распределения случайного вектора 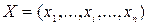 и математическое ожидание оценки
и математическое ожидание оценки  вычисляется по формуле
вычисляется по формуле  . Поскольку
. Поскольку  является несмещенной оценкой параметра
является несмещенной оценкой параметра  , имеем:
, имеем:  . Дифференцируя данное равенство по параметру
. Дифференцируя данное равенство по параметру  , получаем
, получаем  (*). Так как
(*). Так как  - плотность распределения случайного вектора
- плотность распределения случайного вектора 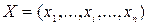 , то верно равенство
, то верно равенство  . Дифференцируя данное равенство по параметру
. Дифференцируя данное равенство по параметру  , получаем
, получаем  . Умножим обе части получившегося равенства на
. Умножим обе части получившегося равенства на  , имеем:
, имеем:  (**). Вычитая из (*) (**), получаем
(**). Вычитая из (*) (**), получаем  . Данное равенство можно преобразовать следующим образом:
. Данное равенство можно преобразовать следующим образом:  ,
,
 .
.
 (***).
(***).
Для любых случайных величин  и
и  выполняется следующее неравенство
выполняется следующее неравенство
 , называемое неравенством Шварца, причем равенство в неравенстве Шварца достигается тогда и только тогда, когда
, называемое неравенством Шварца, причем равенство в неравенстве Шварца достигается тогда и только тогда, когда  с вероятностью 1. Полагая в (***)
с вероятностью 1. Полагая в (***)  ,
,  , получаем:
, получаем:
 (****).
(****).
Но  . Следовательно, верно соотношение
. Следовательно, верно соотношение
 , и доказательство теоремы завершено.
, и доказательство теоремы завершено.
Определение. Несмещенная оценка  параметра
параметра  называется эффективной, если для нее достигается равенство в неравенстве Рао-Крамера, то есть ее вариация минимальна.
называется эффективной, если для нее достигается равенство в неравенстве Рао-Крамера, то есть ее вариация минимальна.
Следствие (Критерий эффективности оценки).
Для того, чтобы несмещенная оценка  параметра
параметра  была эффективной, необходимо и достаточно выполнение равенства
была эффективной, необходимо и достаточно выполнение равенства
 .
.
Доказательство.
Несмещенная оценка  параметра
параметра  является эффективной тогда и только тогда, когда для нее достигается равенство в неравенстве Рао-Крамера, равносильном неравенству (****). Но равенство в неравенстве Шварца достигается тогда и только тогда, когда
является эффективной тогда и только тогда, когда для нее достигается равенство в неравенстве Рао-Крамера, равносильном неравенству (****). Но равенство в неравенстве Шварца достигается тогда и только тогда, когда  с вероятностью 1. Положив
с вероятностью 1. Положив  ,
,  получаем:
получаем:  , что и требовалось доказать.
, что и требовалось доказать.
Рассмотрим примеры применения полученного критерия.
Пример 1. Пусть генеральная совокупность  имеет нормальное распределение с неизвестным математическим ожиданием
имеет нормальное распределение с неизвестным математическим ожиданием  и известной дисперсией
и известной дисперсией  , то есть выполняется равенство
, то есть выполняется равенство  . Тогда для функции правдоподобия
. Тогда для функции правдоподобия  справедлива цепочка равенств:
справедлива цепочка равенств:


 .
.
Логарифмируя данную функцию, получаем:
 .
.
Вычисляя  , имеем:
, имеем:

 .
.
Таким образом, для оценки  выполнен критерий эффективности, и в данном случае эмпирическое среднее
выполнен критерий эффективности, и в данном случае эмпирическое среднее  является эффективной оценкой математического ожидания генеральной совокупности.
является эффективной оценкой математического ожидания генеральной совокупности.
Пример 2. Пусть генеральная совокупность  имеет распределение Коши с неизвестным параметром
имеет распределение Коши с неизвестным параметром  , то есть верно равенство
, то есть верно равенство  . Тогда имеем:
. Тогда имеем:

 ,
,
 ,
,
 .
.
Видно, что в данном случае  нельзя представить в виде
нельзя представить в виде  , и эффективной оценки параметра
, и эффективной оценки параметра  не существует.
не существует.
Контрольные вопросы.
1) Чем отличается вариационный ряд от выборки?
2) Чем отличается гистограмма от полигона?
3) Как вычисляется длина интервала при группировке данных?
4) Что представляют собой числа  ,
,  в интервальном ряду?
в интервальном ряду?
5) Как из интервального ряда можно получить вариационный ряд?
6) Как определяется оценка параметра  ?
?
7) Какая оценка называется несмещенной?
8) Какая оценка называется асимптотически несмещенной?
9) Как определяется эмпирическое среднее?
10) Как определяется эмпирическая дисперсия?
11) Какими свойствами обладает эмпирическое среднее?
12) Какими свойствами обладает эмпирическая дисперсия?
13) Как определяется исправленная эмпирическая дисперсия?
14) Какая оценка называется состоятельной?
15) Как определяется вариация оценки?
16) Каким свойством обладает вариация несмещенной оценки?
17) Как определяется функция правдоподобия для дискретного распределения?
18) Как определяется функция правдоподобия для абсолютно-непрерывного распределения?
19) Как формулируется неравенство Рао-Крамера?
20) Какая оценка называется эффективной?
21) Как формулируется критерий эффективности оценки?

 - оценка параметра
- оценка параметра  . Вариация данной оценки обозначается
. Вариация данной оценки обозначается  и определяется равенством
и определяется равенством  .
. . Имеем:
. Имеем:  , что и требовалось доказать.
, что и требовалось доказать. зависит от неизвестного параметра
зависит от неизвестного параметра 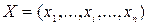 - выборка.
- выборка. и определяется равенством
и определяется равенством  , где
, где  , если генеральная совокупность
, если генеральная совокупность  , если
, если  .
. , называемое неравенством Рао-Крамера.
, называемое неравенством Рао-Крамера. вычисляется по формуле
вычисляется по формуле  . Поскольку
. Поскольку  . Дифференцируя данное равенство по параметру
. Дифференцируя данное равенство по параметру  (*). Так как
(*). Так как  . Дифференцируя данное равенство по параметру
. Дифференцируя данное равенство по параметру  . Умножим обе части получившегося равенства на
. Умножим обе части получившегося равенства на  (**). Вычитая из (*) (**), получаем
(**). Вычитая из (*) (**), получаем  . Данное равенство можно преобразовать следующим образом:
. Данное равенство можно преобразовать следующим образом:  ,
, .
. (***).
(***). выполняется следующее неравенство
выполняется следующее неравенство , называемое неравенством Шварца, причем равенство в неравенстве Шварца достигается тогда и только тогда, когда
, называемое неравенством Шварца, причем равенство в неравенстве Шварца достигается тогда и только тогда, когда  с вероятностью 1. Полагая в (***)
с вероятностью 1. Полагая в (***)  ,
,  , получаем:
, получаем: (****).
(****). . Следовательно, верно соотношение
. Следовательно, верно соотношение .
. и известной дисперсией
и известной дисперсией  , то есть выполняется равенство
, то есть выполняется равенство  . Тогда для функции правдоподобия
. Тогда для функции правдоподобия 

 .
. .
. , имеем:
, имеем:
 .
. выполнен критерий эффективности, и в данном случае эмпирическое среднее
выполнен критерий эффективности, и в данном случае эмпирическое среднее  является эффективной оценкой математического ожидания генеральной совокупности.
является эффективной оценкой математического ожидания генеральной совокупности. . Тогда имеем:
. Тогда имеем:
 ,
, ,
, .
. нельзя представить в виде
нельзя представить в виде  , и эффективной оценки параметра
, и эффективной оценки параметра  ,
,  в интервальном ряду?
в интервальном ряду?


