Когда мы строим «точечную» оценку  неизвестного параметра
неизвестного параметра  генеральной совокупности
генеральной совокупности  , то, даже если она обладает всеми хорошими свойствами (несмещенность, состоятельность, эффективность), то все равно практически никогда не будет выполняться равенство
, то, даже если она обладает всеми хорошими свойствами (несмещенность, состоятельность, эффективность), то все равно практически никогда не будет выполняться равенство  . Поэтому возникла идея не оценивать неизвестный параметр
. Поэтому возникла идея не оценивать неизвестный параметр  одним числом
одним числом  , а строить интервал со случайными границами, содержащий неизвестный параметр с заранее заданной вероятностью
, а строить интервал со случайными границами, содержащий неизвестный параметр с заранее заданной вероятностью  , близкой к 1. Такие интервалы называются доверительными интервалами. Дадим точное определение доверительного интервала.
, близкой к 1. Такие интервалы называются доверительными интервалами. Дадим точное определение доверительного интервала.
Определение. Пусть распределение генеральной совокупности  зависит от неизвестного параметра
зависит от неизвестного параметра  ,
,  и
и  - две измеримые функции выборки, удовлетворяющее условию
- две измеримые функции выборки, удовлетворяющее условию  ,
,  . Тогда интервал со случайными границами
. Тогда интервал со случайными границами  называется доверительным интервалом для параметра
называется доверительным интервалом для параметра  с уровнем доверия
с уровнем доверия  , если выполняется условие
, если выполняется условие  .
.
Замечание. Значение уровня доверия  берется близким к 1, например,
берется близким к 1, например,  ;
;  ;
;  ;
;  .
.
Рассмотрим примеры построения доверительных интервалов.
Пример 1. Пусть генеральная совокупность  имеет нормальное распределение с неизвестным математическим ожиданием
имеет нормальное распределение с неизвестным математическим ожиданием  и известной дисперсией
и известной дисперсией  (то есть распределение
(то есть распределение  ). Построим доверительный интервал для неизвестного параметра
). Построим доверительный интервал для неизвестного параметра  . По теореме о распределении выборочных характеристик из нормальной совокупности случайная величина
. По теореме о распределении выборочных характеристик из нормальной совокупности случайная величина  имеет распределение
имеет распределение  . Следовательно, случайная величина
. Следовательно, случайная величина  имеет распределение
имеет распределение  . Отсюда для любого
. Отсюда для любого 
 получаем равенство
получаем равенство
 , где
, где  - функция Лапласа, определяемая равенством
- функция Лапласа, определяемая равенством  . Следовательно, если задать
. Следовательно, если задать  , то по таблицам функции Лапласа можно найти число
, то по таблицам функции Лапласа можно найти число  , для которого выполняется равенство
, для которого выполняется равенство  или
или  . Проведя элементарные преобразования, получаем:
. Проведя элементарные преобразования, получаем:

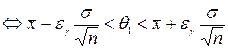 .
.
Таким образом, для любого уровня доверия  по таблицам функции Лапласа можно найти такое число
по таблицам функции Лапласа можно найти такое число  , для которого выполняется равенство
, для которого выполняется равенство
 .
.
Это равенство означает, что интервал со случайными границами  является доверительным интервалом для параметра
является доверительным интервалом для параметра  с уровнем доверия
с уровнем доверия  .
.
Замечание. Длина данного доверительного интервала равна  . Она возрастает с увеличением уровня доверия
. Она возрастает с увеличением уровня доверия  и среднего квадратического отклонения
и среднего квадратического отклонения  и убывает с увеличением числа опытов
и убывает с увеличением числа опытов  .
.
Пример 2. Пусть генеральная совокупность  имеет нормальное распределение с известным математическим ожиданием
имеет нормальное распределение с известным математическим ожиданием  и неизвестной дисперсией
и неизвестной дисперсией 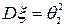 . По теореме о распределении выборочных характеристик из нормальной совокупности случайная величина
. По теореме о распределении выборочных характеристик из нормальной совокупности случайная величина  имеет распределение хи-квадрат с числом степеней свободы
имеет распределение хи-квадрат с числом степеней свободы  (распределение
(распределение  ). Зададим уровень доверия
). Зададим уровень доверия  , определим число
, определим число  равенством
равенством  и по таблицам распределения Стьюдента найдем такие числа
и по таблицам распределения Стьюдента найдем такие числа  и
и  , для которых выполняются равенства
, для которых выполняются равенства  ;
;  . Откуда вытекает неравенство
. Откуда вытекает неравенство  . Преобразовав данное неравенство, получим:
. Преобразовав данное неравенство, получим:  . Таким образом, имеем:
. Таким образом, имеем:  . Данное неравенство означает, что интервал со случайными границами
. Данное неравенство означает, что интервал со случайными границами  является доверительным интервалом для параметра
является доверительным интервалом для параметра  с уровнем доверия
с уровнем доверия  .
.
Пример 3. Пусть генеральная совокупность  имеет нормальное распределение с неизвестным математическим ожиданием
имеет нормальное распределение с неизвестным математическим ожиданием  и неизвестной дисперсией
и неизвестной дисперсией 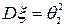 (то есть распределение
(то есть распределение  ). Построим доверительные интервалы для неизвестных параметров
). Построим доверительные интервалы для неизвестных параметров  и
и  .
.
Поскольку доверительный интервал для параметра 
 , построенный в примере 2, не содержит неизвестного параметра
, построенный в примере 2, не содержит неизвестного параметра  , то его можно использовать и в данном случае.
, то его можно использовать и в данном случае.
Доверительный интервал для параметра 
 содержит неизвестное в данном случае среднее квадратическое отклонение
содержит неизвестное в данном случае среднее квадратическое отклонение  , поэтому сейчас мы его использовать не можем. Для построения доверительного интервала для параметра
, поэтому сейчас мы его использовать не можем. Для построения доверительного интервала для параметра  воспользуемся теоремой о распределении выборочных характеристик нормальной совокупности. По этой теореме случайная величина
воспользуемся теоремой о распределении выборочных характеристик нормальной совокупности. По этой теореме случайная величина  имеет распределение Стьюдента с числом степеней свободы
имеет распределение Стьюдента с числом степеней свободы  (распределение
(распределение 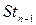 ). Следовательно, по заданному уровню доверия
). Следовательно, по заданному уровню доверия  по таблицам распределения Стьюдента можно найти такое число
по таблицам распределения Стьюдента можно найти такое число  , для которого выполняется равенство
, для которого выполняется равенство  . Проведя преобразования, аналогичные преобразованиям примера 1, получим равенство
. Проведя преобразования, аналогичные преобразованиям примера 1, получим равенство
 .
.
Данное равенство означает, что интервал со случайными границами  является доверительным интервалом для параметра
является доверительным интервалом для параметра  с уровнем доверия
с уровнем доверия  .
.

 неизвестного параметра
неизвестного параметра  генеральной совокупности
генеральной совокупности  , то, даже если она обладает всеми хорошими свойствами (несмещенность, состоятельность, эффективность), то все равно практически никогда не будет выполняться равенство
, то, даже если она обладает всеми хорошими свойствами (несмещенность, состоятельность, эффективность), то все равно практически никогда не будет выполняться равенство  . Поэтому возникла идея не оценивать неизвестный параметр
. Поэтому возникла идея не оценивать неизвестный параметр  , а строить интервал со случайными границами, содержащий неизвестный параметр с заранее заданной вероятностью
, а строить интервал со случайными границами, содержащий неизвестный параметр с заранее заданной вероятностью  , близкой к 1. Такие интервалы называются доверительными интервалами. Дадим точное определение доверительного интервала.
, близкой к 1. Такие интервалы называются доверительными интервалами. Дадим точное определение доверительного интервала. и
и  - две измеримые функции выборки, удовлетворяющее условию
- две измеримые функции выборки, удовлетворяющее условию  ,
,  . Тогда интервал со случайными границами
. Тогда интервал со случайными границами  называется доверительным интервалом для параметра
называется доверительным интервалом для параметра  .
. ;
;  ;
;  ;
;  .
. и известной дисперсией
и известной дисперсией  (то есть распределение
(то есть распределение  ). Построим доверительный интервал для неизвестного параметра
). Построим доверительный интервал для неизвестного параметра  . По теореме о распределении выборочных характеристик из нормальной совокупности случайная величина
. По теореме о распределении выборочных характеристик из нормальной совокупности случайная величина  имеет распределение
имеет распределение  . Следовательно, случайная величина
. Следовательно, случайная величина  имеет распределение
имеет распределение  . Отсюда для любого
. Отсюда для любого 
 получаем равенство
получаем равенство , где
, где  - функция Лапласа, определяемая равенством
- функция Лапласа, определяемая равенством  . Следовательно, если задать
. Следовательно, если задать  , то по таблицам функции Лапласа можно найти число
, то по таблицам функции Лапласа можно найти число  , для которого выполняется равенство
, для которого выполняется равенство  или
или  . Проведя элементарные преобразования, получаем:
. Проведя элементарные преобразования, получаем:
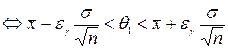 .
. .
. является доверительным интервалом для параметра
является доверительным интервалом для параметра  с уровнем доверия
с уровнем доверия  . Она возрастает с увеличением уровня доверия
. Она возрастает с увеличением уровня доверия  и убывает с увеличением числа опытов
и убывает с увеличением числа опытов  .
. и неизвестной дисперсией
и неизвестной дисперсией 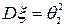 . По теореме о распределении выборочных характеристик из нормальной совокупности случайная величина
. По теореме о распределении выборочных характеристик из нормальной совокупности случайная величина  имеет распределение хи-квадрат с числом степеней свободы
имеет распределение хи-квадрат с числом степеней свободы  (распределение
(распределение  ). Зададим уровень доверия
). Зададим уровень доверия  равенством
равенством  и по таблицам распределения Стьюдента найдем такие числа
и по таблицам распределения Стьюдента найдем такие числа  и
и  , для которых выполняются равенства
, для которых выполняются равенства  ;
;  . Откуда вытекает неравенство
. Откуда вытекает неравенство  . Преобразовав данное неравенство, получим:
. Преобразовав данное неравенство, получим:  . Таким образом, имеем:
. Таким образом, имеем:  . Данное неравенство означает, что интервал со случайными границами
. Данное неравенство означает, что интервал со случайными границами  является доверительным интервалом для параметра
является доверительным интервалом для параметра  с уровнем доверия
с уровнем доверия  ). Построим доверительные интервалы для неизвестных параметров
). Построим доверительные интервалы для неизвестных параметров  , поэтому сейчас мы его использовать не можем. Для построения доверительного интервала для параметра
, поэтому сейчас мы его использовать не можем. Для построения доверительного интервала для параметра  имеет распределение Стьюдента с числом степеней свободы
имеет распределение Стьюдента с числом степеней свободы 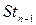 ). Следовательно, по заданному уровню доверия
). Следовательно, по заданному уровню доверия  , для которого выполняется равенство
, для которого выполняется равенство  . Проведя преобразования, аналогичные преобразованиям примера 1, получим равенство
. Проведя преобразования, аналогичные преобразованиям примера 1, получим равенство .
. является доверительным интервалом для параметра
является доверительным интервалом для параметра 


