В прошлой теме были введены основные понятия теории проверки гипотез и рассмотрен критерий знаков проверки однородности генеральных совокупностей. Сейчас мы рассмотрим еще несколько критериев, а именно критерии Пирсона, Смирнова и Колмогорова.
Критерий Пирсона (критерий хи-квадрат). Пусть имеется генеральная совокупность  , распределение которой неизвестно. Относительно распределения данной генеральной совокупности выдвигаются две гипотезы: основная
, распределение которой неизвестно. Относительно распределения данной генеральной совокупности выдвигаются две гипотезы: основная  и альтернативная
и альтернативная  . Основная гипотеза
. Основная гипотеза  состоит в том, что распределение
состоит в том, что распределение  задается данной функцией распределения F, то есть
задается данной функцией распределения F, то есть  . Альтернативная гипотеза
. Альтернативная гипотеза  состоит в том, что
состоит в том, что  . Для проверки данной гипотезы множество R разбивают на l непересекающихся отрезков
. Для проверки данной гипотезы множество R разбивают на l непересекающихся отрезков  . Для единообразия обозначим
. Для единообразия обозначим  ,
,  . Подсчитаем вероятности попаданий значений случайной величины
. Подсчитаем вероятности попаданий значений случайной величины  в отрезок
в отрезок  ,
,  при верной гипотезе
при верной гипотезе  . Имеем,
. Имеем,  ,
,  . Затем проведем эксперимент, получим в результате данного эксперимента выборку
. Затем проведем эксперимент, получим в результате данного эксперимента выборку  и подсчитаем частоты
и подсчитаем частоты  попаданий выборочных значений в интервал
попаданий выборочных значений в интервал  ,
,  . Эти частоты вычисляются по формуле
. Эти частоты вычисляются по формуле 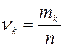 , где
, где  - количество попаданий выборочных значений в интервал
- количество попаданий выборочных значений в интервал  ,
,  . При верной гипотезе
. При верной гипотезе  частоты
частоты  должны быть «близки» к вероятностям
должны быть «близки» к вероятностям  . Для оценки меры этой близости построим величину
. Для оценки меры этой близости построим величину  . Если положить
. Если положить  ,
,  , то получим:
, то получим: 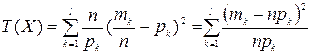 . Выбор именно таких значений
. Выбор именно таких значений  ,
,  , объясняется следующей теоремой, которую мы примем без доказательства.
, объясняется следующей теоремой, которую мы примем без доказательства.
Теорема Пирсона. Если верна гипотеза  и объем выборки стремится к
и объем выборки стремится к  , то распределение
, то распределение  сходится к хи-квадрат с числом степеней свободы
сходится к хи-квадрат с числом степеней свободы  (
(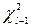 ).
).
Проверка гипотезы по критерию Пирсона производится следующим образом. Строятся интервалы  ,
,  и вычисляются теоретические вероятности
и вычисляются теоретические вероятности  попадания значений случайной величины
попадания значений случайной величины  в данные интервалы. Задается уровень значимости
в данные интервалы. Задается уровень значимости  и по таблицам распределения
и по таблицам распределения  находится такое число
находится такое число  , для которого выполняется неравенство
, для которого выполняется неравенство  . Затем проводится опыт, получают выборку
. Затем проводится опыт, получают выборку  и вычисляют
и вычисляют  ,
,  и
и  . Если выполняется неравенство
. Если выполняется неравенство  , то гипотеза
, то гипотеза  отвергается на уровне значимости
отвергается на уровне значимости  (так как произошло событие, вероятность которого при верной гипотезе
(так как произошло событие, вероятность которого при верной гипотезе  очень мала). Если же справедливо соотношение
очень мала). Если же справедливо соотношение  , то гипотеза
, то гипотеза  не отвергается на уровне значимости
не отвергается на уровне значимости  (но может быть отвергнута на некотором другом уровне значимости).
(но может быть отвергнута на некотором другом уровне значимости).
Критерий Колмогорова. Перед рассмотрением данного критерия нам понадобится ввести следующее определение.
Определение. Пусть  - выборка объема
- выборка объема  из генеральной совокупности
из генеральной совокупности  . Эмпирическая функция распределения обозначается
. Эмпирическая функция распределения обозначается  и равна отношению
и равна отношению  - количества выборочных значений, меньших
- количества выборочных значений, меньших  , к объему выборки, то есть
, к объему выборки, то есть  .
.
Замечание. Эмпирическая функция распределения совпадает с функцией распределения случайной величины  , распределение которой задается таблицей
, распределение которой задается таблицей
 .
.
Эмпирическая функция распределения стремится с увеличением числа опытов к функции распределения генеральной совокупности  .
.
Теперь перейдем непосредственно к рассмотрению критерия Колмогорова. Основной гипотезой  здесь, как и в критерии Пирсона, является предположение, что функцией распределения генеральной совокупности является заданная функция распределения
здесь, как и в критерии Пирсона, является предположение, что функцией распределения генеральной совокупности является заданная функция распределения  , только здесь на
, только здесь на  накладывается требование непрерывности. Альтернативная гипотеза
накладывается требование непрерывности. Альтернативная гипотеза  состоит в том, что
состоит в том, что  . Для проверки данной гипотезы проводится эксперимент, результатом которого является выборка
. Для проверки данной гипотезы проводится эксперимент, результатом которого является выборка  объема
объема  и вычисляется
и вычисляется  . Критерий Колмогорова опирается на следующую теорему, которую мы сформулируем без доказательства.
. Критерий Колмогорова опирается на следующую теорему, которую мы сформулируем без доказательства.
Теорема Колмогорова. Если верно равенство  и
и  - непрерывна, то для любого
- непрерывна, то для любого  справедливо соотношение
справедливо соотношение  , где
, где  - функция Колмогорова, определяемая равенством
- функция Колмогорова, определяемая равенством  .
.
Проверка гипотезы по критерию Колмогорова производится следующим образом. Задается уровень значимости  и по таблицам критерия Колмогорова находится число
и по таблицам критерия Колмогорова находится число  , удовлетворяющее условию
, удовлетворяющее условию  . Затем проводят опыт, получают выборку
. Затем проводят опыт, получают выборку  и вычисляют
и вычисляют  и
и  . Если выполняется неравенство
. Если выполняется неравенство  , то гипотеза
, то гипотеза  отвергается на уровне значимости
отвергается на уровне значимости  (так как произошло событие, маловероятное при верной гипотезе
(так как произошло событие, маловероятное при верной гипотезе  ). Если же справедливо соотношение
). Если же справедливо соотношение  , то гипотеза
, то гипотеза  не отвергается на уровне значимости
не отвергается на уровне значимости  .
.
Замечание. Если верна гипотеза  и
и  , то верно равенство
, то верно равенство  с вероятностью 1, и, следовательно,
с вероятностью 1, и, следовательно, 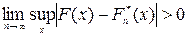 с вероятностью 1. Таким образом, с вероятностью 1 в данном случае
с вероятностью 1. Таким образом, с вероятностью 1 в данном случае  . Это означает, что при любом уровне значимости мощность критерия Колмогорова стремится к 1, когда объем выборки неограниченно увеличивается.
. Это означает, что при любом уровне значимости мощность критерия Колмогорова стремится к 1, когда объем выборки неограниченно увеличивается.
Критерий Смирнова. В данном случае имеются две независимые генеральные совокупности  и
и  . Основная гипотеза
. Основная гипотеза  состоит в том, что
состоит в том, что  ; альтернативная гипотеза
; альтернативная гипотеза  состоит в том, что
состоит в том, что  . Предполагается что
. Предполагается что  и
и  непрерывны. Для проверки гипотезы в результате эксперимента получают выборку
непрерывны. Для проверки гипотезы в результате эксперимента получают выборку  объема
объема  из первой генеральной совокупности и выборку
из первой генеральной совокупности и выборку  объема
объема  из второй генеральной совокупности. Затем вычисляют
из второй генеральной совокупности. Затем вычисляют  и
и  и определяют
и определяют  равенством
равенством  . Критерий Смирнова основан на следующей теореме, которую мы сформулируем без доказательства.
. Критерий Смирнова основан на следующей теореме, которую мы сформулируем без доказательства.
Теорема Смирнова. Если  ,
,  - непрерывна и выполняется равенство
- непрерывна и выполняется равенство  ,
,  , то при всех
, то при всех  справедливо соотношение
справедливо соотношение  , где
, где  - функция Колмогорова.
- функция Колмогорова.
Проверка гипотезы по критерию Смирнова осуществляется следующим образом. Задается уровень значимости  и по таблицам распределения Колмогорова находится такое число
и по таблицам распределения Колмогорова находится такое число  , для которого выполняется равенство
, для которого выполняется равенство  . Затем проводится опыт, получаются выборки
. Затем проводится опыт, получаются выборки  и
и 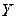 и вычисляется
и вычисляется  . Если справедливо соотношение
. Если справедливо соотношение  , то гипотеза
, то гипотеза  отвергается на уровне значимости
отвергается на уровне значимости  . Если же справедливо соотношение
. Если же справедливо соотношение  , то гипотеза
, то гипотеза  не отвергается на уровне значимости
не отвергается на уровне значимости  .
.
Замечание. При неограниченном возрастании объема выборок мощность критерия Смирнова стремится к 1.
Контрольные вопросы
1) Как определяется доверительный интервал для неизвестного параметра?
2) Как строится доверительный интервал для параметра  , если генеральная совокупность
, если генеральная совокупность  имеет нормальное распределение
имеет нормальное распределение  ?
?
3) Чему равна длина доверительного интервала для параметра  , если генеральная совокупность
, если генеральная совокупность  имеет нормальное распределение
имеет нормальное распределение  ?
?
4) Как строится доверительный интервал для параметра  , если генеральная совокупность
, если генеральная совокупность  имеет распределение
имеет распределение  ?
?
5) Как строится доверительный интервал для параметра  , если генеральная совокупность
, если генеральная совокупность  имеет нормальное распределение
имеет нормальное распределение  ?
?
6) Как строится доверительный интервал для параметра  , если генеральная совокупность
, если генеральная совокупность  имеет распределение
имеет распределение  ?
?
7) Можно ли доверительный интервал, построенный для  при ξ ~
при ξ ~  использовать для оценивания
использовать для оценивания  при ξ ~
при ξ ~  ? Почему?
? Почему?
8) Можно ли доверительный интервал, построенный для  при ξ ~
при ξ ~  использовать для оценивания
использовать для оценивания  при ξ ~
при ξ ~  ? Почему?
? Почему?
9) Какому условию должно удовлетворять критическое множество  , построенное для проверки основной гипотезы
, построенное для проверки основной гипотезы  для уровня значимости
для уровня значимости  ?
?
10) Как определяется и интерпретируется ошибка первого рода?
11) Как определяется и интерпретируется ошибка второго рода?
12) Как определяется и интерпретируется мощность критерия?
13) Какое распределение используется для нахождения «порогов»  ,
, 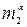 в критерии знаков?
в критерии знаков?
14) Как строится  в критерии Пирсона?
в критерии Пирсона?
15) Какое распределение используется для нахождения «порога»  в критерии Пирсона?
в критерии Пирсона?
16) Как определяется эмпирическая функция распределения?
17) Как строится  в критерии Колмогорова?
в критерии Колмогорова?
18) Какое распределение используется для нахождения «порога»  в критерии Колмогорова?
в критерии Колмогорова?
19) Как строится  в критерии Смирнова?
в критерии Смирнова?
20) Какое распределение используется для нахождения «порога»  в критерии Смирнова?
в критерии Смирнова?

 , распределение которой неизвестно. Относительно распределения данной генеральной совокупности выдвигаются две гипотезы: основная
, распределение которой неизвестно. Относительно распределения данной генеральной совокупности выдвигаются две гипотезы: основная  и альтернативная
и альтернативная  . Основная гипотеза
. Основная гипотеза  . Альтернативная гипотеза
. Альтернативная гипотеза  . Для проверки данной гипотезы множество R разбивают на l непересекающихся отрезков
. Для проверки данной гипотезы множество R разбивают на l непересекающихся отрезков  . Для единообразия обозначим
. Для единообразия обозначим  ,
,  . Подсчитаем вероятности попаданий значений случайной величины
. Подсчитаем вероятности попаданий значений случайной величины  ,
,  при верной гипотезе
при верной гипотезе  ,
,  и подсчитаем частоты
и подсчитаем частоты  попаданий выборочных значений в интервал
попаданий выборочных значений в интервал 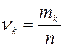 , где
, где  - количество попаданий выборочных значений в интервал
- количество попаданий выборочных значений в интервал  . Для оценки меры этой близости построим величину
. Для оценки меры этой близости построим величину  . Если положить
. Если положить  ,
,  , то получим:
, то получим: 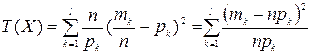 . Выбор именно таких значений
. Выбор именно таких значений  ,
,  , то распределение
, то распределение  сходится к хи-квадрат с числом степеней свободы
сходится к хи-квадрат с числом степеней свободы  (
(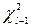 ).
). и по таблицам распределения
и по таблицам распределения  находится такое число
находится такое число  , для которого выполняется неравенство
, для которого выполняется неравенство  . Затем проводится опыт, получают выборку
. Затем проводится опыт, получают выборку  , то гипотеза
, то гипотеза  , то гипотеза
, то гипотеза  из генеральной совокупности
из генеральной совокупности  и равна отношению
и равна отношению  - количества выборочных значений, меньших
- количества выборочных значений, меньших  , к объему выборки, то есть
, к объему выборки, то есть  .
. , распределение которой задается таблицей
, распределение которой задается таблицей .
. , только здесь на
, только здесь на  . Для проверки данной гипотезы проводится эксперимент, результатом которого является выборка
. Для проверки данной гипотезы проводится эксперимент, результатом которого является выборка  . Критерий Колмогорова опирается на следующую теорему, которую мы сформулируем без доказательства.
. Критерий Колмогорова опирается на следующую теорему, которую мы сформулируем без доказательства. справедливо соотношение
справедливо соотношение  , где
, где  - функция Колмогорова, определяемая равенством
- функция Колмогорова, определяемая равенством  .
. , то верно равенство
, то верно равенство  с вероятностью 1, и, следовательно,
с вероятностью 1, и, следовательно, 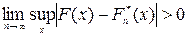 с вероятностью 1. Таким образом, с вероятностью 1 в данном случае
с вероятностью 1. Таким образом, с вероятностью 1 в данном случае  . Это означает, что при любом уровне значимости мощность критерия Колмогорова стремится к 1, когда объем выборки неограниченно увеличивается.
. Это означает, что при любом уровне значимости мощность критерия Колмогорова стремится к 1, когда объем выборки неограниченно увеличивается. ; альтернативная гипотеза
; альтернативная гипотеза  . Предполагается что
. Предполагается что  и
и  непрерывны. Для проверки гипотезы в результате эксперимента получают выборку
непрерывны. Для проверки гипотезы в результате эксперимента получают выборку  объема
объема  из второй генеральной совокупности. Затем вычисляют
из второй генеральной совокупности. Затем вычисляют  и определяют
и определяют  равенством
равенством  . Критерий Смирнова основан на следующей теореме, которую мы сформулируем без доказательства.
. Критерий Смирнова основан на следующей теореме, которую мы сформулируем без доказательства. ,
,  ,
,  , то при всех
, то при всех  , где
, где  . Затем проводится опыт, получаются выборки
. Затем проводится опыт, получаются выборки  и
и 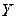 и вычисляется
и вычисляется  , то гипотеза
, то гипотеза  , то гипотеза
, то гипотеза  , если генеральная совокупность
, если генеральная совокупность  ?
? , если генеральная совокупность
, если генеральная совокупность  ?
? ?
? ?
? использовать для оценивания
использовать для оценивания  при ξ ~
при ξ ~  использовать для оценивания
использовать для оценивания  , построенное для проверки основной гипотезы
, построенное для проверки основной гипотезы  ?
? ,
, 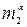 в критерии знаков?
в критерии знаков? в критерии Пирсона?
в критерии Пирсона? в критерии Смирнова?
в критерии Смирнова?


