ТЕМА 6. Распределение выборочных характеристик нормальной совокупности
В данной теме будет рассмотрена нормальная генеральная совокупность и найдено распределение ее важнейших характеристик. Полученные результаты будут широко применяться при построении доверительных интервалов и проверке статистических гипотез. Поскольку доказательство некоторых фактов требует глубокого знания линейной алгебры, в частности, теории квадратичных форм, часть утверждений следующей теоремы будет приведена без доказательства. Теорема (о распределении выборочных характеристик нормальной совокупности). Пусть генеральная совокупность 1) 2) 3) 4) Доказательство. 1) Данное утверждение примем без доказательства. 2) Поскольку
Следовательно, 3) Данное утверждение примем без доказательства. 4) Так как из второго утверждения теоремы
Из третьего утверждения теоремы случайная величина Таким образом, действительно случайная величина Доказательство теоремы завершено.
Контрольные вопросы 1) Как определяются моменты случайной величины и от чего они зависят? 2) Как определяются эмпирические моменты и от чего они зависят? 3) В чем состоит основная идея метода моментов? 4) Чему равна оценка параметра распределения Пуассона, найденная по методу моментов? Совпадает ли она с оценкой этого же параметра, найденной по методу наибольшего правдоподобия? 5) Чему равна оценка параметра показательного распределения, найденная по методу моментов? Совпадает ли она с оценкой этого же параметра, найденной по методу наибольшего правдоподобия? 6) Каким свойством логарифма руководствуемся, переходя от функции правдоподобия к ее логарифму? 7) Всегда ли оценку наибольшего правдоподобия можно находить с помощью уравнения правдоподобия? 8) Всегда ли решение уравнения правдоподобия дает оценку наибольшего правдоподобия? 9) Каким условиям должны удовлетворять случайные величины 10) Каким условиям должны удовлетворять случайные величины 11) Каким условиям должны удовлетворять случайные величины 12) Как формулируется теорема сложения для распределения 13) Если 14) Если 15) Если
|

 имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами  (
( ),
),  - выборка объема n из данной генеральной совокупности,
- выборка объема n из данной генеральной совокупности,  - эмпирическое среднее,
- эмпирическое среднее,  - эмпирическая дисперсия,
- эмпирическая дисперсия,  . Тогда справедливы следующие утверждения:
. Тогда справедливы следующие утверждения: и
и  независимы,
независимы, (
( ),
), имеет распределение
имеет распределение  -квадрат с n-1 степенью свободы (
-квадрат с n-1 степенью свободы ( ),
), имеет распределение Стьюдента с n-1 степенью свободы (
имеет распределение Стьюдента с n-1 степенью свободы ( ).
). можно рассматривать как независимые случайные величины, имеющие то же распределение, что и генеральная совокупность
можно рассматривать как независимые случайные величины, имеющие то же распределение, что и генеральная совокупность 

 . Поскольку каждая
. Поскольку каждая  ,
,  имеет нормальное распределение, то их линейная комбинация
имеет нормальное распределение, то их линейная комбинация  ,
, .
. имеет нормальное распределение с параметрами 0, 1. Действительно, нормальность данной случайной величины вытекает из нормальности
имеет нормальное распределение с параметрами 0, 1. Действительно, нормальность данной случайной величины вытекает из нормальности  ,
,  .
. имеет распределение
имеет распределение  . Преобразуем данную случайную величину. Имеем:
. Преобразуем данную случайную величину. Имеем:  .
.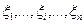 для того, чтобы случайная величина
для того, чтобы случайная величина 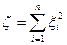 имела распределение
имела распределение  ?
? для того, чтобы случайная величина
для того, чтобы случайная величина  имела распределение
имела распределение  ?
?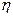 для того, чтобы случайная величина
для того, чтобы случайная величина 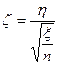 имеет распределение
имеет распределение  имеет распределение
имеет распределение  имеет распределение
имеет распределение 


