ТЕМА 2. Оценки параметров распределений. Несмещенные и состоятельные оценки. Эмпирическое среднее и эмпирическая дисперсия, их свойства
Часто распределение случайной величины зависит от одного или нескольких параметров. Например, если ξ имеет распределение Пуассона с параметром λ > 0, то при всех m =0, 1… выполняется равенство Часто бывает, что вид распределения известен, а неизвестны только параметры. Возникает задача оценки неизвестного параметра на основе опытных данных. Неизвестный параметр в математической статистике принято обозначать греческой буквой θ. Определение. Пусть распределение случайной величины ξ зависит от неизвестного параметра θ. Оценкой данного параметра называется измеримая функция от выборки Замечание. Если выборочные значения Замечание. Если требуется подчеркнуть зависимость оценки от объема выборки n, то применяют обозначение Для того чтобы оценка Определение. Оценка Определение. Оценка Несмещенность оценки означает, что она в среднем совпадает с оцениваемым параметром. Рассмотрим примеры наиболее часто применяемых оценок. Определение. Эмпирическое (выборочное) среднее обозначается Эмпирическое среднее является оценкой математического ожидания генеральной совокупности ξ. Определение. Эмпирическая (выборочная) дисперсия обозначается s2 и определяется равенством Эмпирическая дисперсия является оценкой дисперсии генеральной совокупности ξ. Теорема. Эмпирическое среднее является несмещенной оценкой математического ожидания генеральной совокупности ξ;. Эмпирическая дисперсия является смещенной, но асимптотически несмещенной оценкой дисперсии генеральной совокупности ξ. Доказательство. Для доказательства первого утверждения теоремы нужно проверить выполнение равенства
Имеем: Перейдем к доказательству второго утверждения теоремы. Сначала докажем равенство
Теперь подсчитаем
(так как
Так как Мs2≠ σ 2. то s2 является смещенной оценкой Dξ =σ 2. Так как Замечание. Из доказательства теоремы вытекает, что оценка Определение. Оценка Определение. Оценка Состоятельность оценки означает, что с увеличением числа опытов она сходится по вероятности к оцениваемому параметру. Теорема. Эмпирическое среднее Доказательство. Как уже отмечалось, выборочные значения
Но по закону больших чисел имеем
и первое утверждение теоремы доказано. Квадраты выборочных значений
Используя равенство
Следовательно,
|

 . Меняя λ, мы будем получать различные распределения Пуассона. Если же случайная величина ξ имеет нормальное распределение с параметрами a и σ, то ее плотность задается равенством
. Меняя λ, мы будем получать различные распределения Пуассона. Если же случайная величина ξ имеет нормальное распределение с параметрами a и σ, то ее плотность задается равенством  .
. .
. рассматривать как независимые случайные величины, имеющие то же распределение, что и генеральная совокупность ξ, то оценка
рассматривать как независимые случайные величины, имеющие то же распределение, что и генеральная совокупность ξ, то оценка 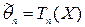 .
. оценивала параметр θ, она должна обладать определенными свойствами.
оценивала параметр θ, она должна обладать определенными свойствами. . В противном случае оценка называется смещенной.
. В противном случае оценка называется смещенной.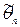 параметра θ называется асимптотически несмещенной, если выполняется равенство
параметра θ называется асимптотически несмещенной, если выполняется равенство  .
. и определяется равенством
и определяется равенством 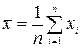 .
.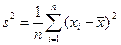 .
. , где
, где 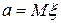 . Поскольку
. Поскольку 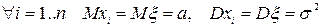 .
.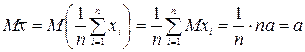 , и первое утверждение теоремы доказано.
, и первое утверждение теоремы доказано. . Действительно, верна цепочка равенств
. Действительно, верна цепочка равенств
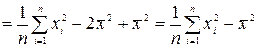 , которая доказывает наше утверждение.
, которая доказывает наше утверждение. . Имеем:
. Имеем: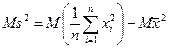 . Но
. Но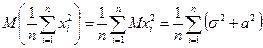
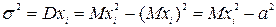 ).
).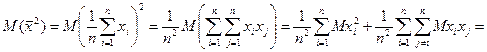
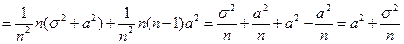 . (Здесь, пользуясь независимостью случайных величин
. (Здесь, пользуясь независимостью случайных величин 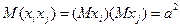 ). Таким образом, получаем:
). Таким образом, получаем: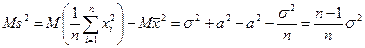 .
.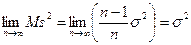 , то s2 является асимптотически несмещенной оценкой Dξ =σ 2. Доказательство теоремы завершено.
, то s2 является асимптотически несмещенной оценкой Dξ =σ 2. Доказательство теоремы завершено.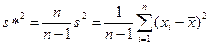 является несмещенной оценкой дисперсии генеральной совокупности ξ.
является несмещенной оценкой дисперсии генеральной совокупности ξ.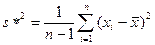 называется исправленной эмпирической дисперсией.
называется исправленной эмпирической дисперсией. называется состоятельной, если выполняется условие
называется состоятельной, если выполняется условие  ,
, 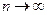 , что означает справедливость соотношения
, что означает справедливость соотношения 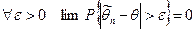 .
. является состоятельной оценкой математического ожидания генеральной совокупности ξ. Эмпирическая дисперсия S2 является состоятельной оценкой дисперсии генеральной совокупности ξ.
является состоятельной оценкой математического ожидания генеральной совокупности ξ. Эмпирическая дисперсия S2 является состоятельной оценкой дисперсии генеральной совокупности ξ. .
.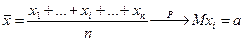 ,
,  можно рассматривать как независимые случайные величины, имеющие то же распределение, что и квадрат генеральной совокупности ξ. Тогда справедливо условие
можно рассматривать как независимые случайные величины, имеющие то же распределение, что и квадрат генеральной совокупности ξ. Тогда справедливо условие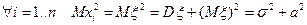 .
.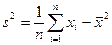 и закон больших чисел, получаем:
и закон больших чисел, получаем: ,
, 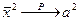 ,
,  и
и  является состоятельной оценкой дисперсии
является состоятельной оценкой дисперсии 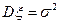 . Доказательство теоремы завершено.
. Доказательство теоремы завершено.


