Качество процессов управления определяется полностью двумя динамическими характеристиками АС, переходной функцией  и амплитудно-частотной характеристикой
и амплитудно-частотной характеристикой  .
.
Переходная функция
Для пояснения физического смысла процесса  рассмотрим фрагмент статической характеристики АС на рис.17. Статическая характеристика показывает, как угловая скорость первичного вала
рассмотрим фрагмент статической характеристики АС на рис.17. Статическая характеристика показывает, как угловая скорость первичного вала  переходит на новый уровень при скачкообразном изменении момента сопротивления
переходит на новый уровень при скачкообразном изменении момента сопротивления 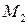 . На рисунке видно, что изменение момента сопротивления происходит на величину
. На рисунке видно, что изменение момента сопротивления происходит на величину 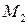 , а соответствующей ему новый уровень угловой скорости определится величиной
, а соответствующей ему новый уровень угловой скорости определится величиной  . Только
. Только 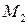 возникает мгновенно, а
возникает мгновенно, а  формируется во времени в виде переходной функции
формируется во времени в виде переходной функции  . Конечные значения
. Конечные значения 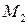 и
и  в безразмерном выражении оба равны единице.
в безразмерном выражении оба равны единице.

 Представляющие каждую из этих единиц параметры определены нами ранее по формуле (13);
Представляющие каждую из этих единиц параметры определены нами ранее по формуле (13);  =1 представляет собой величину 1 рад/с,
=1 представляет собой величину 1 рад/с, 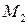 = 1 представляет собой величину 179 Н·м. То есть при мгновенном скачке дорожных сопротивлений на 179 Н·м угловая скорость
= 1 представляет собой величину 179 Н·м. То есть при мгновенном скачке дорожных сопротивлений на 179 Н·м угловая скорость  , изменяясь в виде
, изменяясь в виде  , получит к концу управления изменение на величину 1 рад/с.
, получит к концу управления изменение на величину 1 рад/с.
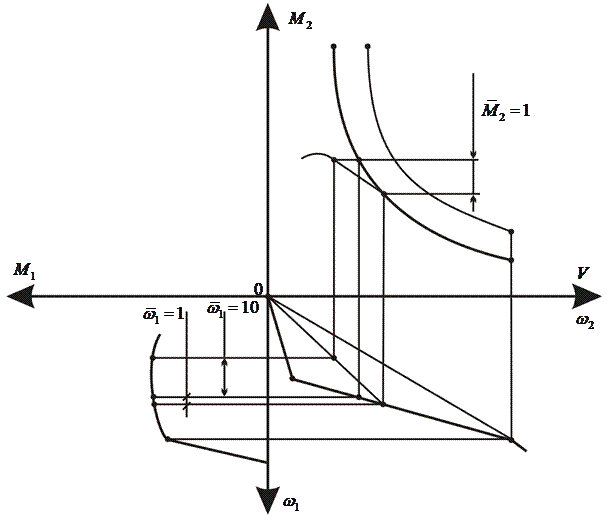
Рис.17. Статические характеристики АС, поясняющей соотношение сигналов возмущающей и управляемой величин в случае отсутствия автоматического управления
Из рис. 17 также видно, что если не управлять бесступенчатой передачей, оставить передаточное число трансмиссии фиксированным, то такой же скачок возмущений ( =1, т.е.
=1, т.е. 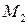 = 179 Н·м) вызывает значительно большее изменение
= 179 Н·м) вызывает значительно большее изменение  , которая равна
, которая равна  .
.
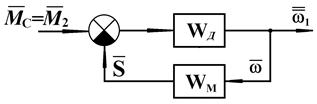
Для оценки  рассмотрим структурную схему машины, в которой нет регулятора и сервопривода, а рычаг управления бесступенчатой передачей закреплен неподвижно (рис.18):
рассмотрим структурную схему машины, в которой нет регулятора и сервопривода, а рычаг управления бесступенчатой передачей закреплен неподвижно (рис.18):
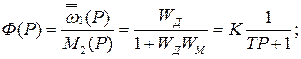 (22)
(22)
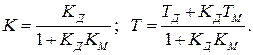 (23)
(23)

Определим численные значения коэффициентов:
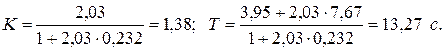
Сравнивая численные значения коэффициентов усиления передаточной функции машины при управлении передачей, формула (10)  = 0, 1375 и для машины с фиксированным передаточным числом, формула (23)
= 0, 1375 и для машины с фиксированным передаточным числом, формула (23)  = 1, 38, заключаем, что во втором случае представляющий параметр
= 1, 38, заключаем, что во втором случае представляющий параметр  будет в данном случае в десять раз больше. Если в первом случае безразмерные значения нагрузки и скорости были приняты равными единице каждое, то во втором случае при безразмерной нагрузке
будет в данном случае в десять раз больше. Если в первом случае безразмерные значения нагрузки и скорости были приняты равными единице каждое, то во втором случае при безразмерной нагрузке 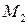 =1 значение безразмерной скорости к достижению установившегося движения будет
=1 значение безразмерной скорости к достижению установившегося движения будет  =10. Все это хорошо видно на статической характеристике (рис. 17).
=10. Все это хорошо видно на статической характеристике (рис. 17).
Отсутствие управления бесступенчатой передачей эквивалентно бездействию гидросервопривода либо, другими словами, его бесконечному замедлению, т.е. соответствует постоянной времени сервопривода  = ∞.
= ∞.
Покажем теперь преимущество автоматического управления трансмиссией. Для этого с целью сопоставления найдем переходную функцию процесса изменения ω 1 при скачкообразном возмущении 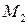 , когда нет управления трансмиссией. Из формулы (22) определим вещественную частотную характеристику при
, когда нет управления трансмиссией. Из формулы (22) определим вещественную частотную характеристику при  =1:
=1:
 (24)
(24)
График 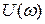 показан на рис. 15 штрихпунктирной линией. Пользуясь таблицами
показан на рис. 15 штрихпунктирной линией. Пользуясь таблицами 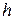 - функций, можно построить переходный процесс
- функций, можно построить переходный процесс  , т.е. при
, т.е. при 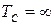 .
.
Покажем и сравним в одном масштабе времени (рис. 19) реальные переходные процессы изменения  от значения
от значения 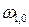 = 268 рад/с до установившегося уровня для двух условий (рис. 17). Кривую переходного процесса при максимальном быстродействии сервопривода (
= 268 рад/с до установившегося уровня для двух условий (рис. 17). Кривую переходного процесса при максимальном быстродействии сервопривода (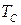 = 0) перенесем с рис. 16, а кривую изменения ω 1 ври фиксированном передаточном числе трансмиссии (
= 0) перенесем с рис. 16, а кривую изменения ω 1 ври фиксированном передаточном числе трансмиссии (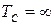 ) построим по ВЧХ, формула (24). Подчеркнем, еще раз, что кривые являются результатом одного и того же по величине скачка возмущений
) построим по ВЧХ, формула (24). Подчеркнем, еще раз, что кривые являются результатом одного и того же по величине скачка возмущений 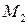 = 179 Н·м, представляющего безразмерную единицу возмущения.
= 179 Н·м, представляющего безразмерную единицу возмущения.
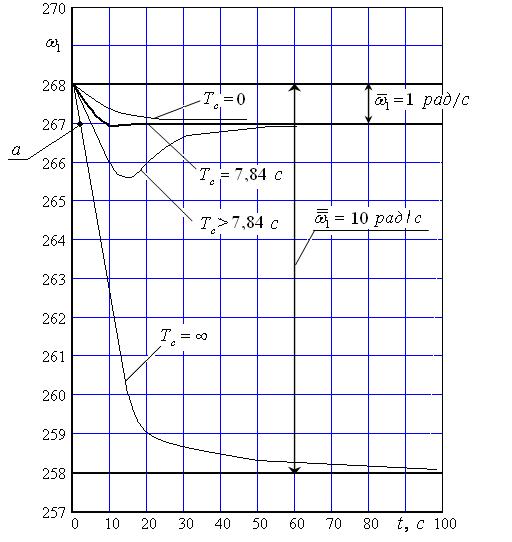
Рис. 19. Переходные процессы в автоматической системе и для случая отсутствия автоматического управления (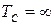 ) в реальных представляющих параметрах управляемой величины
) в реальных представляющих параметрах управляемой величины 
Из рис. 19 видно, что падение скорости  в передаче, где нет управления, будет в 10 раз больше и происходит оно за большее время. Таким образом, автоматическое управление трансмиссией (переходный процесс при
в передаче, где нет управления, будет в 10 раз больше и происходит оно за большее время. Таким образом, автоматическое управление трансмиссией (переходный процесс при 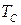 = 7, 84) стабилизирует скорость
= 7, 84) стабилизирует скорость  , а следовательно и мощность двигателя, на высоком уровне по сравнению с машиной без автоматического управления (переходный процесс при
, а следовательно и мощность двигателя, на высоком уровне по сравнению с машиной без автоматического управления (переходный процесс при 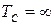 ).
).
Выбор оптимальной постоянной времени сервопривода 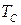 .
.
На рис. 19 показаны переходные процессы при различных выбранных величинах 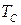 , в том числе при значении, определенном нами как оптимальное –
, в том числе при значении, определенном нами как оптимальное – 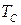 = 7, 84 с. Сравнение кривых переходного процесса при изменении
= 7, 84 с. Сравнение кривых переходного процесса при изменении 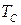 от 0 до ∞ выявляет на первый взгляд парадоксальный смысл принятого решения: снизить быстродействие сервопривода для увеличения быстродействия АС в целом.
от 0 до ∞ выявляет на первый взгляд парадоксальный смысл принятого решения: снизить быстродействие сервопривода для увеличения быстродействия АС в целом.
При 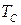 = 0, когда сервопривод действует мгновенно, передаточное число бесступенчатой передачи непрерывно изменяется в строгом соответствии с уменьшающейся скоростью
= 0, когда сервопривод действует мгновенно, передаточное число бесступенчатой передачи непрерывно изменяется в строгом соответствии с уменьшающейся скоростью  . Загрузка двигателя минимальна, и системе остается только ждать, когда инертная машина уменьшит скорость в соответствии с изменившимся скачкообразно дорожными условиями, т. е. вместе со скоростью
. Загрузка двигателя минимальна, и системе остается только ждать, когда инертная машина уменьшит скорость в соответствии с изменившимся скачкообразно дорожными условиями, т. е. вместе со скоростью 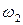 и
и  уменьшит величину до заданного нового уровня
уменьшит величину до заданного нового уровня  = 267 рад/с в апериодическом процессе.
= 267 рад/с в апериодическом процессе.
При 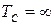 изменяется также апериодически и еще медленнее, но при десятикратном уровне конечного изменения, т.е. до уровня
изменяется также апериодически и еще медленнее, но при десятикратном уровне конечного изменения, т.е. до уровня  = 258 рад/с. А вот уровень, соответствующий
= 258 рад/с. А вот уровень, соответствующий  = 267 рад/с, достигается очень быстро (точка
= 267 рад/с, достигается очень быстро (точка  на рис.19), за время порядка 1, 4 с. Если бы на этом уровне удалось мгновенно изменить передаточное число трансмиссии в соответствии с изменившаяся на величину 179 Н·м сопротивлением, то процесс управления можно было бы считать законченным. И быстродействие было бы очень высоким:
на рис.19), за время порядка 1, 4 с. Если бы на этом уровне удалось мгновенно изменить передаточное число трансмиссии в соответствии с изменившаяся на величину 179 Н·м сопротивлением, то процесс управления можно было бы считать законченным. И быстродействие было бы очень высоким:  = 1, 4 с! Очевидно, что следует организовать замедление действия сервопривода. Правда, по конструкции АС мы не можем вначале исключить действие регулятора и сервопривода, а через 1, 4 с организовать их мгновенное быстродействие, но просто замедлить действие сервопривода - можем, и делаем это, увеличивая его постоянную времени
= 1, 4 с! Очевидно, что следует организовать замедление действия сервопривода. Правда, по конструкции АС мы не можем вначале исключить действие регулятора и сервопривода, а через 1, 4 с организовать их мгновенное быстродействие, но просто замедлить действие сервопривода - можем, и делаем это, увеличивая его постоянную времени 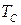 до значения 7, 84 с. В этом случае при управлении передаточное число трансмиссии вначале, при отставании сервопривода, несколько меньше, чем при
до значения 7, 84 с. В этом случае при управлении передаточное число трансмиссии вначале, при отставании сервопривода, несколько меньше, чем при 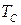 = 0, и оба вала машины, первичный и вторичный, тормозятся быстрее. К концу процесса управления передаточное число все же достигает требуемого значения и ω 1 выравнивается на требуемом уровне: 267 рад/с. При
= 0, и оба вала машины, первичный и вторичный, тормозятся быстрее. К концу процесса управления передаточное число все же достигает требуемого значения и ω 1 выравнивается на требуемом уровне: 267 рад/с. При 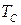 > 7, 83 с достижение требуемого уровня становится все более быстрым, но при этом, как видно из рис. 19, увеличивается перерегулирование, а вместе с перерегулированием и длительность переходного процесса.
> 7, 83 с достижение требуемого уровня становится все более быстрым, но при этом, как видно из рис. 19, увеличивается перерегулирование, а вместе с перерегулированием и длительность переходного процесса.
Возможно ли дальнейшее увеличение быстродействия в рассматриваемой АС, если того требует техническое задание? Из приведенных рассуждений следует, что невозможно. Но если в АС ввести корректирующие обратные связи с дифференцирующими звеньями, вырабатывающими сигналы, пропорциональные дифференциалу управляемой величины, т.е. 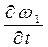 , то быстродействие можно увеличить. Сигналы
, то быстродействие можно увеличить. Сигналы 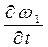 , складываясь с сигналом
, складываясь с сигналом  , вначале изменяют передаточное число в противоположном описанному направлении, интенсивно тормозя двигатель и машину, а в конце цикла управления усиливают сигнал ∆
, вначале изменяют передаточное число в противоположном описанному направлении, интенсивно тормозя двигатель и машину, а в конце цикла управления усиливают сигнал ∆  , обеспечивая быстрый выход управляемой величины на заданный уровень. Применение дифференцирующих звеньев позволяет достигнуть любого наперед заданного быстродействия АС в пределах располагаемой для управления мощности.
, обеспечивая быстрый выход управляемой величины на заданный уровень. Применение дифференцирующих звеньев позволяет достигнуть любого наперед заданного быстродействия АС в пределах располагаемой для управления мощности.
ЛИТЕРАТУРА
1. Болдырев, Р.Н. Расчет автоматической системы класса «мощность»: учебное пособие / Р.Н. Болдырев, С.В. Федоров С.В. – Челябинск: ЧПИ, 1976. – 34 с.
2. Васильев, Д. В. Основа теории и расчета следящих систем / Д. В. Васильев, Г.С. Филиппов. – М.; Л.: Госэнергоиздат, 1959. – 382 с.
3. Петров, В.А. Автоматические системы транспортных машин. – М.: Машиностроение, 1974. – 336 с.
4. Петров, В.А. Автоматическое управление бесступенчатых передач самоходных машин. – М.: Машиностроение, 1986. – 248 с.
5. Болдырев, Р.Н. Расчет автоматической системы класса «мощность»: учебное пособие. – Челябинск: ЧПИ, 1987. – 53 с.

 и амплитудно-частотной характеристикой
и амплитудно-частотной характеристикой  .
. переходит на новый уровень при скачкообразном изменении момента сопротивления
переходит на новый уровень при скачкообразном изменении момента сопротивления 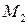 . На рисунке видно, что изменение момента сопротивления происходит на величину
. На рисунке видно, что изменение момента сопротивления происходит на величину 

 =1, т.е.
=1, т.е.  .
.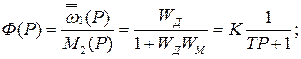 (22)
(22)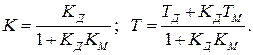 (23)
(23)

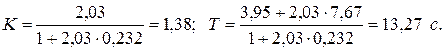
 = 0, 1375 и для машины с фиксированным передаточным числом, формула (23)
= 0, 1375 и для машины с фиксированным передаточным числом, формула (23)  = ∞.
= ∞. (24)
(24)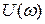 показан на рис. 15 штрихпунктирной линией. Пользуясь таблицами
показан на рис. 15 штрихпунктирной линией. Пользуясь таблицами 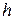 - функций, можно построить переходный процесс
- функций, можно построить переходный процесс 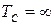 .
.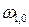 = 268 рад/с до установившегося уровня для двух условий (рис. 17). Кривую переходного процесса при максимальном быстродействии сервопривода (
= 268 рад/с до установившегося уровня для двух условий (рис. 17). Кривую переходного процесса при максимальном быстродействии сервопривода (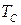 = 0) перенесем с рис. 16, а кривую изменения ω 1 ври фиксированном передаточном числе трансмиссии (
= 0) перенесем с рис. 16, а кривую изменения ω 1 ври фиксированном передаточном числе трансмиссии (
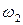 и
и  на рис.19), за время порядка 1, 4 с. Если бы на этом уровне удалось мгновенно изменить передаточное число трансмиссии в соответствии с изменившаяся на величину 179 Н·м сопротивлением, то процесс управления можно было бы считать законченным. И быстродействие было бы очень высоким:
на рис.19), за время порядка 1, 4 с. Если бы на этом уровне удалось мгновенно изменить передаточное число трансмиссии в соответствии с изменившаяся на величину 179 Н·м сопротивлением, то процесс управления можно было бы считать законченным. И быстродействие было бы очень высоким:  = 1, 4 с! Очевидно, что следует организовать замедление действия сервопривода. Правда, по конструкции АС мы не можем вначале исключить действие регулятора и сервопривода, а через 1, 4 с организовать их мгновенное быстродействие, но просто замедлить действие сервопривода - можем, и делаем это, увеличивая его постоянную времени
= 1, 4 с! Очевидно, что следует организовать замедление действия сервопривода. Правда, по конструкции АС мы не можем вначале исключить действие регулятора и сервопривода, а через 1, 4 с организовать их мгновенное быстродействие, но просто замедлить действие сервопривода - можем, и делаем это, увеличивая его постоянную времени 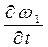 , то быстродействие можно увеличить. Сигналы
, то быстродействие можно увеличить. Сигналы 


