Примеры. 1. Найти ортогональную проекцию и ортогональную составляющую вектора на линейное подпространство L
1. Найти ортогональную проекцию
Нетрудно убедиться, что
Заметьте, что векторы
2. Требуется найти расстояние от точки, заданной вектором
Расстояние между точкой
Для вычисления расстояния удобно перейти к параметрическому уравнению плоскости. Имеем
где
Затем
Векторы
Правая часть этого неравенства и есть искомое расстояние. Осталось вычислить вектор 3. Пусть
с равенством тогда и только тогда, когда Так как
Далее,
или
С равенством тогда и только тогда, когда Задачи 1. Показать, что в пространстве Rn скалярное произведение векторов
где 2. Применяя процесс ортогонализации, построить ортогональный базис подпространства, натянутого на данную систему векторов: а)
б)
3. Найти векторы, дополняющие следующую систему векторов до ортонормированного базиса 4. Найти базис ортогонального дополнения
5. Линейное подпространство L задано уравнениями
Найти уравнения, задающие ортогональное дополнение 6. Показать, что задание линейного подпространства L пространства En и его ортогонального дополнения 7. Доказать, что
Найти ортогональную проекцию 8.
9.
10. Найти расстояние от точки, заданной вектором
11. Найти расстояние между двумя плоскостями
ЛИТЕРАТУРА 1. Воеводин В. В. Линейная алгебра. — М.: «Наука», 1974. — 400 с. 2. Ефимов Н. В., Розендорн Э. Р. Линейная алгебра и многомерная геометрия. — М.: «Наука», 1974. — 250 с. 3. Проскуряков И. В. Сборник задач по линейной алгебре. — М.: «Наука», 1970. — 355 с.
СОДЕРЖАНИЕ 1. Линейные пространства. Определение 3 1.1. Задачи 4 2. Линейная зависимость. Базис и координаты вектора 5 2.1. Задачи 10 3. Подпространства линейного пространства 11 3.1. Задачи 16 4. Точечно-векторное аффинное пространство 19 4.1.Система координат в пространстве 4.2. Прямая и плоскость в 4.3. Задачи 23 5. Евклидовы и унитарные пространства 25 5.1.Ортонормированный базис евклидова и унитарного пространств 27 5.2.Ортогональное дополнение 30 5.3. Проектирование вектора на подпространства 31 5.4. Задачи 35 Литература 37
|

 и ортогональную составляющую
и ортогональную составляющую  вектора
вектора  на линейное подпространство L, натянутое на векторы
на линейное подпространство L, натянутое на векторы  . Все векторы заданы координатами относительно ортонормированного базиса.
. Все векторы заданы координатами относительно ортонормированного базиса. ,
, 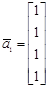 ,
,  ,
, 
 и что за базис можно принять векторы
и что за базис можно принять векторы  и
и  . Нам будет удобно перейти к ортонормированному базису в L. Применяя процедуру ортогонализации к векторам
. Нам будет удобно перейти к ортонормированному базису в L. Применяя процедуру ортогонализации к векторам  ,
, 
 и
и  линейно выражаются через
линейно выражаются через 
 до плоскости (линейного многообразия), заданной системой уравнений
до плоскости (линейного многообразия), заданной системой уравнений
 и множеством L определится следующим образом
и множеством L определится следующим образом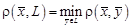
 и поэтому всякий вектор
и поэтому всякий вектор  представляется в виде
представляется в виде
 — фиксированный радиус-вектор точки плоскости;
— фиксированный радиус-вектор точки плоскости;  и
и  — базис направляющего линейного подпространства, которое задается соответствующей однородной системой. Решая уравнение, получим, например,
— базис направляющего линейного подпространства, которое задается соответствующей однородной системой. Решая уравнение, получим, например, ,
,  ,
, 

 . Так как
. Так как  , а
, а  , то
, то
 и найти его норму. Проделав для этого аналогичные вычисления и вычислив длину вектора, получим, что
и найти его норму. Проделав для этого аналогичные вычисления и вычислив длину вектора, получим, что  .
. — ортонормированная система векторов евклидова пространства En. Нужно доказать, что для любого вектора
— ортонормированная система векторов евклидова пространства En. Нужно доказать, что для любого вектора  имеет место неравенство Бесселя
имеет место неравенство Бесселя
 , т.е. векторы
, т.е. векторы  образуют ортонормированный базис в En.
образуют ортонормированный базис в En. — ортонормированная система, то ее всегда можно векторами
— ортонормированная система, то ее всегда можно векторами  достроить до ортонормированного базиса в En. Разложим вектор
достроить до ортонормированного базиса в En. Разложим вектор 




 или когда
или когда  .
. и
и 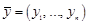 может быть определено выражением
может быть определено выражением
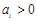 .
. ,
,  ,
, 
 ,
,  ,
,  ,
, 
 ,
,  .
. подпространства L, натянутого на векторы:
подпространства L, натянутого на векторы: ,
,  ,
, 
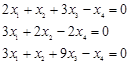

 и ортогональную составляющую
и ортогональную составляющую  вектора
вектора  , а L натянуто на векторы
, а L натянуто на векторы ;
;  ,
, 
 , а L задано системой уравнений
, а L задано системой уравнений
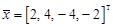 до плоскости (линейного многообразия), заданного системой уравнений
до плоскости (линейного многообразия), заданного системой уравнений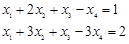
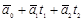 и
и  , где
, где ,
,  ,
,  ,
, ,
, 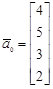 ,
, 
 19
19


