Примеры. 1. Пространство V3. В этом пространстве всякие три некомпланарных вектора линейно независимы, а всякие четыре вектора линейно зависимы
1. Пространство V 3. В этом пространстве всякие три некомпланарных вектора линейно независимы, а всякие четыре вектора линейно зависимы. Следовательно, 2. Пространство Rn. В этом пространстве всякие Если в линейном пространстве X существует базис из n векторов, то Всякие два базиса
где невырожденные матрицы Если
Пример: Доказать, что каждая из данных двух систем векторов является базисом R 3 и найти связь координат одного и того же вектора
Для доказательства того, что данные системы векторов являются базисными, вычислим, как и в предыдущем примере, ранги матриц
Нетрудно убедиться, что
Откуда получаем систему девяти скалярных уравнений
Решая системы уравнений, получаем матрицу перехода
и связь между «старыми»
Задачи 1. Доказать, что если система векторов 2. Доказать, что если часть из векторов Векторы 3.
4.
5.
6. Доказать, что каждая из двух систем векторов является базисом, и найти связь координат одного и того же вектора в этих двух базисах.
7. Доказать линейную независимость системы функций 8. Определить размерность линейного пространства квадратных матриц n -го порядка. 9. Как изменится матрица перехода от одного базиса к другому, если: а) поменять местами два вектора первого базиса; б) поменять местами два вектора второго базиса; в) записать векторы обоих базисов в обратном порядке?
|

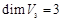 .
. вектор линейно зависимы и существуют системы из n линейно независимых векторов, например, система векторов (2). Следовательно,
вектор линейно зависимы и существуют системы из n линейно независимых векторов, например, система векторов (2). Следовательно, 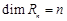
 , обратно, если
, обратно, если  и
и 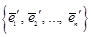 пространства X связаны между собой симметричными формулами
пространства X связаны между собой симметричными формулами
 (2.4)
(2.4)
 (2.5)
(2.5) и
и  являются взаимно обратными, i -й столбец матрицы A образуют координаты вектора
являются взаимно обратными, i -й столбец матрицы A образуют координаты вектора  в базисе из векторов
в базисе из векторов  . Формулы (2.4) и (2.5) называются формулами перехода, матрицы A и
. Формулы (2.4) и (2.5) называются формулами перехода, матрицы A и  — матрицами перехода.
— матрицами перехода. и
и  – координаты вектора
– координаты вектора  в базисах
в базисах  , соответственно, то
, соответственно, то


 и
и 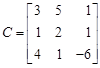
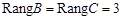 , и, следовательно, в R 3 данные системы векторов образуют базисы. Для определения связи координат необходимо получить формулы перехода (2.4) и (2.5). Имеем
, и, следовательно, в R 3 данные системы векторов образуют базисы. Для определения связи координат необходимо получить формулы перехода (2.4) и (2.5). Имеем




 и «новыми»
и «новыми»  координатами:
координатами:
 содержит нулевой вектор, то совокупность векторов линейно зависима.
содержит нулевой вектор, то совокупность векторов линейно зависима. ,
,  ,
, 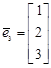 ,
, 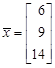
 ,
,  ,
, 
 ,
,  ,
,  ,
,  ,
, 
 ,
,  ,
,  ,
, 
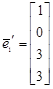 ,
,  ,
,  ,
, 
 , где
, где  – попарно различные действительные числа.
– попарно различные действительные числа.


