Примеры. 1. Рассмотрим пространство геометрических векторов V3
1. Рассмотрим пространство геометрических векторов V 3. В нем два вектора линейно зависимы, когда они коллинеарны; три вектора линейно зависимы, когда они компланарны. Всякие четыре вектора этого пространства всегда линейно зависимы. 2. Рассмотрим арифметическое пространство Rn. Попытаемся построить линейно независимую систему векторов этого пространства. Рассмотрим k векторов
Если
где
Получаем в результате относительно ti систему n линейных однородных уравнений с k неизвестными и матрицей
и имеет ненулевое решение, если
Отсюда следует, что в пространстве Rn не может быть больше, чем n линейно независимых векторов. Линейно независимыми являются всякие векторы, компоненты которых образуют матрицу полного ранга. Например, n векторов
Определение. Совокупность линейно независимых векторов
Соотношение (2.3) называется разложением вектора В силу линейной независимости векторов базиса разложение (2.3) определяется единственным образом. Определение. Коэффициенты Пример. Совокупность векторов (2.2) образует очевидно базис пространства Rn, так как для всякого вектора
При решении задач полезно помнить, что векторы линейно зависимы тогда и только тогда, когда линейно зависимы вектор-столбцы из их координат относительно произвольного базиса. Определение. Если в линейном пространстве X существует n линейно независимых векторов, а всякие
Само линейное пространство X называется при этом n -мерным. Линейное пространство, в котором можно указать сколь угодно большое число линейно независимых векторов называется бесконечно мерным.
|

 ,
, 
 линейно зависимы, то
линейно зависимы, то  одновременно такие, что
одновременно такие, что
 – ноль пространства Rn. По определению Rn отсюда следует, что
– ноль пространства Rn. По определению Rn отсюда следует, что ,
, 
 размера
размера 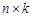 . Такая система имеет только нулевое решение, если
. Такая система имеет только нулевое решение, если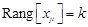
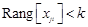
 (2.2)
(2.2) пространства X называется базисом этого пространства, если
пространства X называется базисом этого пространства, если 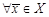 найдутся такие числа
найдутся такие числа  , что справедливо равенство
, что справедливо равенство (2.3)
(2.3) по базису.
по базису. разложения вектора
разложения вектора  называются координатами вектора
называются координатами вектора  имеет место разложение
имеет место разложение
 вектор этого пространства линейно зависимы, то число, n называется размерностью линейного пространства
вектор этого пространства линейно зависимы, то число, n называется размерностью линейного пространства



