Примеры. 1. Необходимо найти условия, необходимые и достаточные для того, чтобы две прямые и пространства лежали в одной двумерной плоск
1. Необходимо найти условия, необходимые и достаточные для того, чтобы две прямые
где λ1, λ2 — параметры. Тогда при некоторых
а при некоторых Поэтому вектор
Значит и
Очевидно, что теперь оба уравнения содержатся в уравнении плоскости H:
где t и τ параметры, и, следовательно, прямые принадлежат плоскости H. 2. Найти необходимые и достаточные условия для того, чтобы две прямые Предположим, что при некоторых значениях параметров
Отсюда следует, что векторы
единственно. Значит ранг матрицы системы равен 2 и векторы Задачи 1. Найти точку пересечения двух прямых
а)
б)
2. Найти прямую, проходящую через точку, заданную вектором а) б) 3. Описать все случаи взаимного расположения двух плоскостей
в n -мерном пространстве и указать необходимые и достаточные условия для каждого из этих случаев. 4. Доказать, что всякая система 5. Доказать, что линейное многообразие может быть охарактеризовано как множество векторов, содержащее вместе с любыми двумя векторами 6. Найти параметрические уравнения плоскости, заданной общими уравнениями:
7. Найти общие уравнения плоскости, заданной параметрическими уравнениями в координатной форме
|

 и
и  пространства
пространства  лежали в одной двумерной плоскости.
лежали в одной двумерной плоскости. Предположим вначале, что две данные прямые лежат в одной плоскости с уравнением
Предположим вначале, что две данные прямые лежат в одной плоскости с уравнением
 ,
,  ,
,  ,
, ,
,  ,
,  .
. принадлежит линейной оболочке векторов
принадлежит линейной оболочке векторов  и
и  . Далее для произвольной точки 1 прямой найдутся такие λ1 и λ2, что
. Далее для произвольной точки 1 прямой найдутся такие λ1 и λ2, что
 . Аналогично
. Аналогично  . Но всякие три вектора из двумерного подпространства линейно зависимы. Следовательно, необходимым условием принадлежности прямых плоскости является линейная зависимость векторов
. Но всякие три вектора из двумерного подпространства линейно зависимы. Следовательно, необходимым условием принадлежности прямых плоскости является линейная зависимость векторов  . Обратно, пусть
. Обратно, пусть 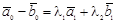 . Поэтому уравнение второй прямой можно переписать в виде
. Поэтому уравнение второй прямой можно переписать в виде
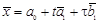
 и
и  проходили через одну точку, но не совпадали.
проходили через одну точку, но не совпадали. для первой прямой и
для первой прямой и  для второй прямые пересекаются. Тогда
для второй прямые пересекаются. Тогда
 рассматривать как систему линейных уравнений (в координатной форме) на определение t 1 и t 2. Так как прямые не совпадают, то решение системы
рассматривать как систему линейных уравнений (в координатной форме) на определение t 1 и t 2. Так как прямые не совпадают, то решение системы (4.1)
(4.1) должны быть линейно независимы. Обратно пусть
должны быть линейно независимы. Обратно пусть  и
и  .
. ,
,  ,
,  ,
, 
 ,
,  ,
,  ,
, 
 и пересекающую прямые
и пересекающую прямые  ,
,  ,
,  ,
,  ,
, 
 ,
,  ,
,  ,
,  ,
, 
 ,
, 
 точки пространства Vn определяет плоскость размерности
точки пространства Vn определяет плоскость размерности  .
.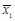 и
и 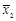 их линейные комбинации
их линейные комбинации  при любых α.
при любых α.




