Примеры
1. Рассмотрим векторы пространства Rn, координаты которых удовлетворяют уравнению
Покажем, что они образуют линейное подпространство в Rn. Пусть
и для координат векторов
2. Рассмотрим подмножество симметричных матриц линейного пространства квадратных матриц n -го порядка. Покажем, что они образуют линейное подпространство. Пусть Основные свойства линейных подпространств вытекают из следующих утверждений: Размерность всякого линейного подпространства L пространства X не превосходит размерности самого пространства. Если в подпространстве L Координаты
ранга n-k. Определение. Пусть M – подмножество векторов пространства X. Совокупность всех линейных комбинаций векторов из М называется линейной оболочной L(M) векторов М. Всякая линейная оболочка является линейным подпространством. Размерность линейной оболочки L (M), натянутой на векторы множества M, равна числу линейно независимых векторов данного множества. Определение. Суммой L двух подпространств L 1 и L 2 одного и того же пространства X называется множество векторов вида Сумма линейных подпространств Определение. Пересечением L линейных подпространств L 1 и L 2 называется совокупность векторов, принадлежащих одновременно L 1 и L 2. Обозначается Пересечение линейных подпространств Определение. Прямой суммой L двух подпространств L 1 и L 2 называется сумма этих подпространств при условии, что их пересечение состоит лишь из нулевого вектора. Обозначается Размерности суммы и пересечения подпространств L 1 и L 2 связаны между собой следующим соотношением
Примеры 1. Определим размерность и базис линейного подпространства, натянутого на следующие векторы, заданные своими координатами
Для определения размерности линейной оболочки нужно определить число линейно независимых векторов в исходной системе. Воспользуемся тем, что векторы линейно независимы тогда и только тогда, когда линейно независимы вектор-столбцы из их координат. Составим матрицу из координат векторов и найдем ее ранг
Ранг матрицы равен трем. Следовательно, 2. Найдем систему линейных уравнений, которая задает линейное подпространство, натянутое на следующую систему векторов, заданных своими координатами в некотором базисе
Для решения задачи удобно найти сначала базис в
Остается перейти теперь к системе уравнений относительно старых координат
где
Исключая
3. Найти размерности и базисы суммы и пересечения линейных подпространств L 1 и L 2, натянутых на векторы, заданные своими координатами:
Нетрудно убедиться, что векторы
Остается найти базисный вектор в М. Пусть
Получаем для значений
Решая эту систему, получим
Вектор Адачи Доказать, что следующие системы векторов из Rn образуют линейные подпространства и найти их размерность и базис: 1. Все n -мерные векторы, у которых первая и последняя координата равны между собой. 2. Все n -мерные векторы, у которых координаты с четными номерами равны нулю. 3. Все n -мерные векторы вида 4. Показать, что всякое линейное пространство есть линейная оболочка любого своего базиса. 5. Показать, что решение системы линейных однородных уравнений с n неизвестными ранга K образуют подпространство Rn размерности 6. Доказать, что если размерность суммы двух линейных подпространств пространства Rn на единицу больше размерности их пересечения, то сумма совпадает с одним из этих подпространств, а пересечение с другим. 7. Доказать, что пространство Rn есть прямая сумма двух линейных подпространств: L 1 — заданного уравнением 8. Найти размерность и базис линейного подпространства, натянутого на следующую систему векторов, заданных своими координатами
9. Найти систему линейных уравнений, задающую линейное подпространство, натянутое на следующую систему векторов:
Найти размерности суммы и пересечения линейных подпространств: L 1, натянутого на векторы 10.
11.
Найти базисы суммы и пересечения линейных подпространств, натянутых на системы векторов 12.
13.
14. Линейным многообразием называется совокупность векторов пространства Rn, координаты которых
Показать, что если к каждому вектору
|

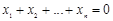 ,
, 
 . Тогда
. Тогда

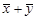 и
и 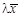 выполняются условия 1 и 2:
выполняются условия 1 и 2:

 и
и 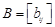 симметричные матрицы. Матрицы
симметричные матрицы. Матрицы  и
и  будут, очевидно, также симметричными, и, следовательно, данное подмножество является линейным подпространством.
будут, очевидно, также симметричными, и, следовательно, данное подмножество является линейным подпространством.
 пространства X
пространства X 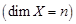 задан базис
задан базис  , то его можно всегда дополнить векторами
, то его можно всегда дополнить векторами 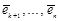 из X так, что система
из X так, что система  образует базис пространства X.
образует базис пространства X.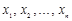 всякого вектора
всякого вектора  k -мерному подпространству n -мерного пространства X в любом базисе удовлетворяют некоторой системе линейных однородных уравнений
k -мерному подпространству n -мерного пространства X в любом базисе удовлетворяют некоторой системе линейных однородных уравнений
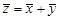 , где
, где  и
и  . Обозначается
. Обозначается  .
. .
. .
.
 ,
,  ,
,  ,
,  ,
, 



 . Базис образуют, например, следующие линейно независимые векторы
. Базис образуют, например, следующие линейно независимые векторы  .
.
 ,
,  ,
, 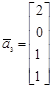
 . Аналогично предыдущей задаче убеждаемся, что базис образуют векторы
. Аналогично предыдущей задаче убеждаемся, что базис образуют векторы  и
и  , например. Некоторыми векторами
, например. Некоторыми векторами  и
и 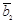 достроим базис
достроим базис  . В новом базисе любой вектор
. В новом базисе любой вектор  из L будет иметь координаты, удовлетворяющие системе уравнений
из L будет иметь координаты, удовлетворяющие системе уравнений
 вектора
вектора  относительно базиса
относительно базиса  . Они будут связаны с новыми координатами формулами перехода
. Они будут связаны с новыми координатами формулами перехода ,
,  ,
,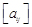 – матрица перехода от
– матрица перехода от 
 и
и 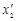 , окончательно получаем
, окончательно получаем

 ,
, 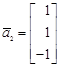 ,
, 

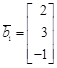 ,
,  ,
, 
 , а всякий вектор из L 2
, а всякий вектор из L 2  . Если
. Если 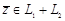 , то
, то 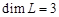 , а базис, например,
, а базис, например,  . Пусть
. Пусть  . Тогда
. Тогда
 , тогда
, тогда  . Значит, существуют такие числа
. Значит, существуют такие числа  и
и  , что
, что

 ,
, 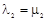 ,
,  , где
, где  - произвольно. Поэтому всякий вектор
- произвольно. Поэтому всякий вектор 
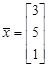 можно принять за базис в
можно принять за базис в  , где a и b — любые числа.
, где a и b — любые числа.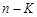 .
. .
. ,
,  ,
,  ,
,  ,
, 
 ,
,  ,
,  ,
, 
 и L 2, натянутого на векторы
и L 2, натянутого на векторы 
 ,
,  ,
,  ,
, 
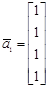 ,
,  ,
,  ,
, 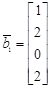 ,
, 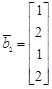 ,
, 
 и
и 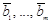
 ,
,  ,
,  ,
,  ,
,  ,
, 
 ,
,  ,
,  ,
,  ,
, 
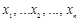 удовлетворяют системе линейных уравнений
удовлетворяют системе линейных уравнений



