Ортонормированный базис евклидова и унитарного пространств
Определение. Вектор Определение. Два вектора Определение. Система векторов
Всякая ортогональная система линейно независима. Определение. Базис евклидова (унитарного) пространства, векторы которого Заметьте себе, что, в зависимости от того, как введено скалярное произведение, различные системы векторов могут быть или не быть ортонормированными. Процедура ортогонализации Грама-Шмидта. Для построения ортонормированной системы векторов и, в частности, ортонормированного базиса
Второй вектор
Наконец, векторы
Пример. Необходимо ортогонализировать систему векторов
Скалярное произведение векторов
Для построения первого вектора
Для построения второго вектора вычислим вначале
и вектор
Для построения третьего вектора вычислим
И вектор
Во всяком ортонормированном базисе
Координаты вектора
|

 называется нормированным, если
называется нормированным, если  .
. называются ортогональными, если
называются ортогональными, если  .
. евклидова (унитарного) пространства называется ортогональной, если она либо состоит из одного ненулевого вектора, либо ее векторы попарно ортогональны. Ортогональная система, состоящая из нормированных векторов, называется ортонормированной. Для нее
евклидова (унитарного) пространства называется ортогональной, если она либо состоит из одного ненулевого вектора, либо ее векторы попарно ортогональны. Ортогональная система, состоящая из нормированных векторов, называется ортонормированной. Для нее
 — линейно независимы. Первый вектор ортонормированной системы
— линейно независимы. Первый вектор ортонормированной системы
 ,
, 

 определяются соотношениями
определяются соотношениями ,
, 
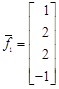 ,
,  ,
, 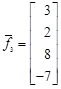
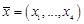 и
и 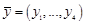 определяется как
определяется как
 считаем
считаем  . Вектор
. Вектор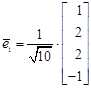
 . Вектор
. Вектор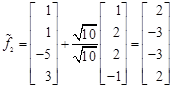

 и
и  . Вектор
. Вектор
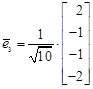
 и
и 





