Евклидовы и унитарные пространства
Определение. Вещественная функция 1. 2. 3. 4. Определение. Вещественное линейное пространство E, на котором задано скалярное произведение, называется евклидовым пространством. Пример. Рассмотрим арифметическое пространство Rn и определим скалярное произведение векторов
Прямой подстановкой убеждаемся, что условия 1-4 выполняются. Получим n -мерное евклидово пространство, которое обычно обозначается как En. В случае комплексного линейного пространства скалярное произведение определяется несколько иным образом. Определение. Комплексная функция 1. 2. 3. 4. Комплексное линейное пространство U, на котором задано скалярное произведение, называется унитарным пространством. Во всяком унитарном (евклидовом) пространстве имеет место неравенство Коши-Шварца:
с равенством лишь в случае, когда Введение скалярного произведения позволяет распространить на линейные пространства различные метрические понятия: 1. Норма (длина) вектора
Введенная функция удовлетворяет следующим условиям 1. 2. 3. 2. Угол φ между векторами
3. Расстояние между точками аффинного пространства
|
двух векторных аргументов 
и 
, заданная на линейном пространстве E, называется скалярным произведением, если выполняются следующие условия:
, 
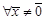и 
соотношением
.
