Производные и дифференциалы высших порядков
1. Частные производные высших порядков Пусть функция z = f (x, y) задана на области G. Пусть на G существуют частные производные
Частные производные
Аналогично определяются частные производные и более высоких порядков. Если известны частные производные (n -1)-го порядка, то частные производные от этих частных производных называются частными производными п-го порядка и обозначаются:
Т.о., частные производные высших порядков определяются индуктивно, т.е. последовательно, начиная от первой. Частные производные Теорема 1. Пусть функция z = f (x, y) и ее частные производные Доказательство.
Введем вспомогательную функцию
Здесь числитель равен разности значений функции f (x, y) в точках сторон АD и В С с одинаковыми абсциссами. Тогда ω; можно записать в виде:
По условию существует
Т.к. функция φ;(х) дифференцируема на отрезке [ x 0; x 0+Δ x ], то она непрерывна на этом отрезке. Следовательно, к ней можно применить формулу Лагранжа:
= Т.к. по условию существует и
где
Теперь вместо функции φ;(х) рассмотрим функцию
Тогда
Применим формулу Лагранжа к функции ψ;(у)на отрезке [ у 0; у 0+Δ у ]:
а затем к функции
Из соотношений (3), (4) следует
Пусть
Т.к. по условию
Тогда, переходя в равенстве (5) к пределу при
Замечание. Утверждение, аналогичное теореме 1, может быть доказано и для смешанных производных любого порядка. Т.е. смешанные производные любого порядка при условии их непрерывности не зависят от порядка дифференцирования, например,
Теорема 2. Если смешанные производные n – го порядка, отличающиеся только порядком дифференцирования, непрерывны на области G, то они на этой области равны.
2. Дифференциалы высших порядков I. Пусть z = f (x; y), где х, у – независимые переменные, определена на области G и имеет на этой области непрерывные частные производные. Тогда она дифференцируема, и ее дифференциал равен
Следовательно, dz – функция четырех переменных: х, у, dx, dy. Зафиксируем dx и dy. Тогда dz = φ;(x; y). Если функция f на G имеет непрерывные частные производные второго порядка, то функция dz = φ;(x; y) на этой области имеет непрерывные частные производные, следовательно, она дифференцируема на G и имеет дифференциал. Определение. Дифференциалом второго порядка d 2 z функции z = f (x; y) называется дифференциал от ее дифференциала первого порядка dz: d 2 z = d (dz).
Т.к.
Символическая запись второго дифференциала: Если функция f на G имеет непрерывные частные производные третьего порядка, то функция d 2 z = ψ;(x; y) на этой области имеет непрерывные частные производные, следовательно, она имеет дифференциал. Дифференциал от этой функции называется дифференциалом третьего порядка функции z = f (x; y) и обозначается d 3 z. Таким образом,
Символическая запись: Если функция f на G имеет непрерывные частные производные n -го порядка, то на G существует дифференциал n -го порядка, и он определяется с. о.: dnz = d (dn- 1 z).
II. Дифференциалы высших порядков от сложной функции. Пусть z = f (x; y) определена на области G, x = φ;(u; v), y = ψ;(u; v) определены на области H, где u, v – независимые переменные, причем "(u; v)Î H
dz – функция от u и v.
Следовательно, Вывод. Сравнивая (6) и (7) видим, что дифференциал второго порядка не имеет инвариантной формы. Дифференциалы высших порядков также не обладают свойством инвариантности формы. Частный случай. Пусть z = f (x; y) определена на G,
Значит, dx и dy не зависят от u и v, и поэтому d 2 x = d (dx)=0, d 2 y = d (dy)=0. Подставляя эти равенства в (7), получим (6). Т.о., в частном случае, когда x и y – линейные функции, форма второго дифференциала инвариантна. Аналогично, и формы дифференциалов высших порядков в этом случае инвариантны.
3. Формула Тейлора для функции двух переменных Пусть функция F (t) в некоторой окрестности V (t 0) имеет производные до (n +1)-го порядка включительно. Тогда справедлива формула Тейлора:
Обозначим t-t 0=Δ t, F (t) -F (t 0)=Δ F (t 0), F' (t 0)(t-t 0)= F' (t 0)Δ t = dF (t 0), F'' (t 0)(t-t 0)2= F'' (t 0)(Δ t)2= d 2 F (t 0) и т.д. Тогда (8) можно записать в виде
В виде (9) формула Тейлора распространяется и на случай функций нескольких переменных. Теорема. Пусть функция z = f (x; y), где х, у – независимые переменные, определена и имеет непрерывные частные производные до (n +1)-го порядка включительно в некоторой окрестности точки М (х 0; y 0) Vδ (х 0; y 0). Тогда "Δ х, Δ у, удовлетворяющих условию
Доказательство.
Функция на [0;1] становится сложной функцией от переменной t: f (x; y)= f (х 0+ t Δ x; y 0+ t Δ y)= F (t). (12) По условию f (x; y) имеет непрерывные частные производные до (n +1)-го порядка включительно на Vδ (х 0; y 0). Функции х и у, как линейные, имеют непрерывные производные любого порядка. Поэтому F (t) имеет непрерывные производные до (n +1)-го порядка включительно на [0;1]. Тогда для F (t) на [0;1] справедлива формула Тейлора (9).Положим в ней t 0=1, t 0+Δ t =1, Δ t =1:
Перейдем здесь к f (x; y), используя (12). Δ F (0)= F (1) -F (0)= f (х 0+Δ x; y 0+Δ y) -f (х 0; y 0)=Δ f (х 0; y 0). Форма первого дифференциала инвариантна. Тогда, учитывая (11) при вычислении dx и dy, получим
т.к. dt =Δ t =1. Поскольку х = х 0+ t Δ x, y = y 0+ t Δ y – линейные функции, то дифференциалы высших порядков от функции F (t)= f (x; y) обладают свойством инвариантности.. Следовательно, для их вычисления мы можем использовать простейшую форму:
Аналогично,
Подставляя все выражения в (13), получим (10). Формула Тейлора имеет большое значение при вычислении приращений и значений функции с большой степенью точности.
|

 и
и  . Они называются частными производными первого порядка функции f. Эти производные на G являются функциями от x и y:
. Они называются частными производными первого порядка функции f. Эти производные на G являются функциями от x и y:  ,
,  . Они тоже могут иметь частные производные G. Частные производные этих функций φ; и ψ; называются частными производными второго порядка функции f:
. Они тоже могут иметь частные производные G. Частные производные этих функций φ; и ψ; называются частными производными второго порядка функции f: ,
, ,
, ,
, .
. и
и  взяты по различным переменным, они называются смешанными. Если частные производные второго порядка определены на G, то они сами являются функциями от x и y и могут иметь частные производные по этим переменным. Частные производные от частных производных второго порядка называются частными производными третьего порядка функции f и обозначаются:
взяты по различным переменным, они называются смешанными. Если частные производные второго порядка определены на G, то они сами являются функциями от x и y и могут иметь частные производные по этим переменным. Частные производные от частных производных второго порядка называются частными производными третьего порядка функции f и обозначаются: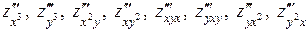 (8 штук, 6 смешанных).
(8 штук, 6 смешанных).
 определены в некоторой окрестности точки (х 0; у 0), и в этой точке
определены в некоторой окрестности точки (х 0; у 0), и в этой точке 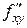 и
и  непрерывны. Тогда
непрерывны. Тогда 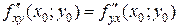 .
. Придадим значениям х 0 и у 0 приращения Δ х и Δ у так, чтобы точка (х 0+Δ х; у 0+Δ у) находилась в окрестности точки (х 0; у 0). Составим выражение
Придадим значениям х 0 и у 0 приращения Δ х и Δ у так, чтобы точка (х 0+Δ х; у 0+Δ у) находилась в окрестности точки (х 0; у 0). Составим выражение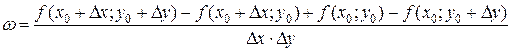 .
. Чтобы легче запомнить, как строится выражение, рассмотрим прямоугольник АBСD с вершинами А (х 0+Δ х; у 0+Δ у), B (х 0+Δ х; у 0), С (х 0; у 0), D (х 0; у 0+Δ у). Тогда числитель равен алгебраической сумме значений функции f (x, y) в вершинах прямоугольника, причем значение в точке А берется со знаком «+», и при обходе прямоугольника против часовой стрелки знаки перед остальными слагаемыми чередуются.
Чтобы легче запомнить, как строится выражение, рассмотрим прямоугольник АBСD с вершинами А (х 0+Δ х; у 0+Δ у), B (х 0+Δ х; у 0), С (х 0; у 0), D (х 0; у 0+Δ у). Тогда числитель равен алгебраической сумме значений функции f (x, y) в вершинах прямоугольника, причем значение в точке А берется со знаком «+», и при обходе прямоугольника против часовой стрелки знаки перед остальными слагаемыми чередуются. .
.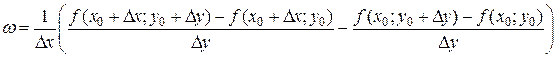 =
=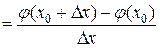 .
. , значит, существует и
, значит, существует и .
.
 , где
, где 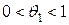 . (1)
. (1) , то к функции
, то к функции  , как к функции от у, на отрезке [ у 0; у 0+Δ у ] можно тоже применить формулу Лагранжа:
, как к функции от у, на отрезке [ у 0; у 0+Δ у ] можно тоже применить формулу Лагранжа: , (2)
, (2) . Тогда из (1) и (2) следует
. Тогда из (1) и (2) следует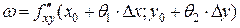 , где
, где  . (3)
. (3) .
. =
= .
.

 ,
, , как к функции от х, на отрезке [ x 0; x 0+Δ x ]:
, как к функции от х, на отрезке [ x 0; x 0+Δ x ]: , где
, где  . (4)
. (4)
 . (5)
. (5) . Тогда
. Тогда ,
,  .
. и
и .
. .
. 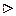
 .
. , где dx =Δ x, dy =Δ y.
, где dx =Δ x, dy =Δ y.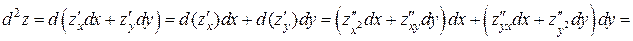
 .
. , то
, то . (6)
. (6) .
. .
.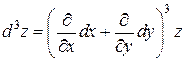 .
. .
. . Тогда
. Тогда  определена на H. Если функция z = f (x; y) имеет непрерывные частные производные n -го порядка на G, и функции x и y имеют непрерывные частные производные n -го порядка на H, то сложная функция h имеет непрерывные частные производные n -го порядка на H. Тогда существуют дифференциалы 1, 2,…, n -го порядков от сложной функции h (u; v) на H.
определена на H. Если функция z = f (x; y) имеет непрерывные частные производные n -го порядка на G, и функции x и y имеют непрерывные частные производные n -го порядка на H, то сложная функция h имеет непрерывные частные производные n -го порядка на H. Тогда существуют дифференциалы 1, 2,…, n -го порядков от сложной функции h (u; v) на H. - функции от u и v),
- функции от u и v), ,
,  ,
,
 .
. . (7)
. (7) , где u, v – независимые переменные, α;1,…, γ;2 – числа. Тогда
, где u, v – независимые переменные, α;1,…, γ;2 – числа. Тогда .
. ,
, .
.
 . (8)
. (8) , где 0< θ;<1. (9)
, где 0< θ;<1. (9)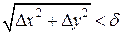 , имеет место формула Тейлора:
, имеет место формула Тейлора:
 , где 0< θ;<1. (10)
, где 0< θ;<1. (10) , где
, где  .
. Тогда ММ 0Î Vδ (х 0; y 0). Параметрические уравнения отрезка ММ 0:
Тогда ММ 0Î Vδ (х 0; y 0). Параметрические уравнения отрезка ММ 0: (11)
(11) . (13)
. (13)
 ,
,
 .
. ,…,
,…,  ,
, .
.


