1. Дифференцирование сложной функции
Пусть функция z = f (x;y) определена в области G Ì  , а х и у сами являются функциями от переменной t: х = φ;(t), у = ψ;(t). Пусть t изменяется в промежутке
, а х и у сами являются функциями от переменной t: х = φ;(t), у = ψ;(t). Пусть t изменяется в промежутке  так, что (х; у)=(φ;(t); ψ;(t))Î G. В этом случае функция
так, что (х; у)=(φ;(t); ψ;(t))Î G. В этом случае функция
z = f (φ;(t); ψ;(t))= F (t) (1)
является сложной функцией одной переменной t.
Теорема 1. Если существуют производные  ,
,  в точке t
в точке t 
 и существуют непрерывные частные производные
и существуют непрерывные частные производные  ,
,  в соответствующей точке (х; у)=(φ;(t); ψ;(t)), то существует производная
в соответствующей точке (х; у)=(φ;(t); ψ;(t)), то существует производная  от сложной функции (1), и она может быть вычислена по формуле:
от сложной функции (1), и она может быть вычислена по формуле:
 . (2)
. (2)
Доказательство.
 Придадим переменной t приращение
Придадим переменной t приращение  тогда x и y получат соответствующие приращения
тогда x и y получат соответствующие приращения  и
и  , а функция z = f (x; у) получит приращение
, а функция z = f (x; у) получит приращение  . Так как z = f (x; у) в точке (x;y) имеет непрерывные частные производные, то по теореме 3 §4 она дифференцируема в этой точке. Следовательно, ее полное приращение может быть записано в следующем виде:
. Так как z = f (x; у) в точке (x;y) имеет непрерывные частные производные, то по теореме 3 §4 она дифференцируема в этой точке. Следовательно, ее полное приращение может быть записано в следующем виде:
 =
=  , где
, где  ,
, 
 .
.
Разделим равенство на  :
:
 . (3)
. (3)
Пусть  . Так как функции х = φ;(t) и у = ψ;(t) дифференцируемы в точке t, то они непрерывны в этой точке. Тогда
. Так как функции х = φ;(t) и у = ψ;(t) дифференцируемы в точке t, то они непрерывны в этой точке. Тогда  при
при  . Значит, и
. Значит, и  ,
,  при
при  . Т.к. функции x и у по условию имеют производные
. Т.к. функции x и у по условию имеют производные  и
и  в точке t, то
в точке t, то
 ,
, 
 .
. 
Это означает, что правая часть (3) имеет предел при  :
:
 .
.
Тогда существует предел и левой части (3) при  :
:  .
.
Переходя в (3) к пределу при  , получим (2).
, получим (2). 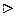
Частный случай:  , то есть
, то есть  . Тогда
. Тогда
 .
.
Пример 1.
z (
x,
y)=

,
x =e

,
y =ln(1
-t). Найти

.
D z определена на  ,
,  . z является функцией от t:
. z является функцией от t:
(*) z (t)=  ,
,  .
.
Вычислим  по формуле (2).
по формуле (2).
 .
.
Но  можно найти и непосредственно из (*). D
можно найти и непосредственно из (*). D
Эффективность дифференцирования по формуле (2) проявляется в более сложных примерах.
Пример2.  .
.
D  .
.
Непосредственно отсюда вычислить  сложно.
сложно.


 …
…
(подставить вместо х и у выражения через t). D
Пример 3.  .
.
D Пусть 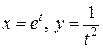 , тогда z = f (x, y), х = φ;(t), у = ψ;(t),
, тогда z = f (x, y), х = φ;(t), у = ψ;(t),
 . D
. D
Пусть теперь функция z = f (x, y) задана в некоторой области G а x и y являются функциями от переменных u и v: 
 . Причём u и v определены в такой области Н, что "(u, v)
. Причём u и v определены в такой области Н, что "(u, v)  Н точка (х, у)=
Н точка (х, у)=  Î G. Тогда z является сложной функцией от переменных u и v:
Î G. Тогда z является сложной функцией от переменных u и v:
 . (4)
. (4)
Теорема 2. Если существуют частные производные  на H и непрерывные частные производные
на H и непрерывные частные производные  на области G, то существуют частные производные
на области G, то существуют частные производные  от сложной функции (4) на H, которые могут быть вычислены по формулам:
от сложной функции (4) на H, которые могут быть вычислены по формулам:
 (5)
(5)
 . (6)
. (6)
Доказательство.
 Пусть (u, v)
Пусть (u, v)  Н. Зафиксируем v. Тогда (4) обращается в сложную функцию одной переменной u вида (1), к которой можно применить теорему 1. На основании этой теоремы
Н. Зафиксируем v. Тогда (4) обращается в сложную функцию одной переменной u вида (1), к которой можно применить теорему 1. На основании этой теоремы
 .
.
Аналогично, фиксируя u, получим сложную функцию одной переменной v:  к которой можно применить теорему 1, получим (6).
к которой можно применить теорему 1, получим (6). 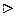
Пример 4. Найти частные производные сложной функции  .
.
D Обозначим  - промежуточные переменные, x, y, z – независимые переменные.
- промежуточные переменные, x, y, z – независимые переменные.
 ,
,
 ,
,
 . D
. D
2. Инвариантность формы дифференциала
I. Пусть z = f (x, y), где x, y – независимые переменные, определена в области G. Пусть на G функция f имеет непрерывные частные производные. Тогда она дифференцируема и её дифференциал
 , (1)
, (1)
где  , т.е. dx, dy – произвольные числа не зависящие от x и y.
, т.е. dx, dy – произвольные числа не зависящие от x и y.
II. Пусть теперь z является сложной функцией от переменных u и v, т.е. z = f (x, y),  ,
,  . Независимые переменные u и v определены в области Н так, что
. Независимые переменные u и v определены в области Н так, что  . Тогда
. Тогда  . Пусть на Н существуют непрерывные частные производные
. Пусть на Н существуют непрерывные частные производные  и на G - непрерывные частные производные
и на G - непрерывные частные производные  и
и  тогда существуют непрерывные частные производные
тогда существуют непрерывные частные производные  и
и  от сложной функции z = h (u, v):
от сложной функции z = h (u, v):
 , (2)
, (2)
 . (3)
. (3)
Тогда сложная функция z = h (u, v) дифференцируема и её дифференциал
 , (4)
, (4)
du, dv – произвольные числа.
Подставляя (2) и (3) в (4), получим

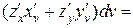
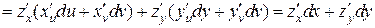 .
.
Итак,  , (5)
, (5)
dx – дифференциал функции  ,
,  ,
,
dy - дифференциал функции  ,
,  .
.
Сравнив (1) и (5), можем сделать вывод. Дифференциал функции f имеет одну и ту же форму относительно x и y:  , как в случае, когда x и y - независимые переменные, так и в случае, когда x и y – функции от других переменных. Это свойство называется инвариантностью формы полного дифференциала. Хотя форма (1) инвариантна (т.е. неизменна), но смысл символов dx и dy не один и тот же. Если x и y - независимые переменные, то dx и dy – числа, не зависящие от x, y. Если же x и y – функции, то dx и dy – дифференциалы этих функций.
, как в случае, когда x и y - независимые переменные, так и в случае, когда x и y – функции от других переменных. Это свойство называется инвариантностью формы полного дифференциала. Хотя форма (1) инвариантна (т.е. неизменна), но смысл символов dx и dy не один и тот же. Если x и y - независимые переменные, то dx и dy – числа, не зависящие от x, y. Если же x и y – функции, то dx и dy – дифференциалы этих функций.
Итак, так как форма (1) инвариантна, то полный дифференциал функции всегда может быть записан в виде (1).
Замечание. Если x и y – независимые переменные, то существуют две формы записи дифференциала:  . Если x и y функции, то
. Если x и y функции, то  .
.
 , x =e
, x =e  , y =ln(1 -t). Найти
, y =ln(1 -t). Найти  .
.

 , а х и у сами являются функциями от переменной t: х = φ;(t), у = ψ;(t). Пусть t изменяется в промежутке
, а х и у сами являются функциями от переменной t: х = φ;(t), у = ψ;(t). Пусть t изменяется в промежутке  так, что (х; у)=(φ;(t); ψ;(t))Î G. В этом случае функция
так, что (х; у)=(φ;(t); ψ;(t))Î G. В этом случае функция ,
,  в точке t
в точке t 
 ,
,  в соответствующей точке (х; у)=(φ;(t); ψ;(t)), то существует производная
в соответствующей точке (х; у)=(φ;(t); ψ;(t)), то существует производная  . (2)
. (2) Придадим переменной t приращение
Придадим переменной t приращение  тогда x и y получат соответствующие приращения
тогда x и y получат соответствующие приращения  и
и  , а функция z = f (x; у) получит приращение
, а функция z = f (x; у) получит приращение  . Так как z = f (x; у) в точке (x;y) имеет непрерывные частные производные, то по теореме 3 §4 она дифференцируема в этой точке. Следовательно, ее полное приращение может быть записано в следующем виде:
. Так как z = f (x; у) в точке (x;y) имеет непрерывные частные производные, то по теореме 3 §4 она дифференцируема в этой точке. Следовательно, ее полное приращение может быть записано в следующем виде: , где
, где  ,
, 
 .
. :
: . (3)
. (3) . Так как функции х = φ;(t) и у = ψ;(t) дифференцируемы в точке t, то они непрерывны в этой точке. Тогда
. Так как функции х = φ;(t) и у = ψ;(t) дифференцируемы в точке t, то они непрерывны в этой точке. Тогда  при
при  ,
,  при
при  ,
, 
 .
.  .
. .
.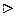
 , то есть
, то есть  . Тогда
. Тогда .
. . z является функцией от t:
. z является функцией от t: ,
,  по формуле (2).
по формуле (2). .
. .
. .
.

 …
… .
.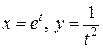 , тогда z = f (x, y), х = φ;(t), у = ψ;(t),
, тогда z = f (x, y), х = φ;(t), у = ψ;(t), . D
. D
 . Причём u и v определены в такой области Н, что "(u, v)
. Причём u и v определены в такой области Н, что "(u, v)  Î G. Тогда z является сложной функцией от переменных u и v:
Î G. Тогда z является сложной функцией от переменных u и v: . (4)
. (4) на H и непрерывные частные производные
на H и непрерывные частные производные  на области G, то существуют частные производные
на области G, то существуют частные производные  от сложной функции (4) на H, которые могут быть вычислены по формулам:
от сложной функции (4) на H, которые могут быть вычислены по формулам: (5)
(5) . (6)
. (6) .
. к которой можно применить теорему 1, получим (6).
к которой можно применить теорему 1, получим (6).  .
. - промежуточные переменные, x, y, z – независимые переменные.
- промежуточные переменные, x, y, z – независимые переменные. ,
, ,
, . D
. D , (1)
, (1) , т.е. dx, dy – произвольные числа не зависящие от x и y.
, т.е. dx, dy – произвольные числа не зависящие от x и y. . Тогда
. Тогда  . Пусть на Н существуют непрерывные частные производные
. Пусть на Н существуют непрерывные частные производные  и
и  от сложной функции z = h (u, v):
от сложной функции z = h (u, v): , (2)
, (2) . (3)
. (3) , (4)
, (4)
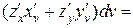
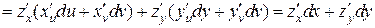 .
. ,
, .
. . Если x и y функции, то
. Если x и y функции, то  .
.


