Экстремум функции нескольких переменных
1. Понятие экстремума, необходимое и достаточное условия Пусть функция z = f (x; y) задана в некоторой окрестности точки M 0(x 0; y 0) V (M 0). Определение 1. Функция z = f (x; y) имеет в точке M 0(x 0; y 0) строгий максимум (строгий минимум), если Определение 2. Функция z = f (x; y) имеет в точке M 0(x 0; y 0) максимум (минимум), если Определение 3. Функция z = f (x; y) имеет в точке M 0(x 0; y 0)(строгий) экстремум, если она имеет в этой точке (строгий) максимум или (строгий) минимум. Точку М 0 называют точкой (строгого) экстремума, а значение функции в ней, т.е. f (M 0) – (строгим) экстремумом. Теорема 1 (необходимое условие экстремума). Пусть функция z = f (x; y) достигает экстремума в точке M 0(x 0; y 0). Если в этой точке существуют частные производные Доказательство.
f (x; y)£ f (х 0; y 0). (1) Рассмотрим точки окрестности Vd (M 0), для которых y=y 0. На этом множестве точек, т.е. на Аналогично, рассмотрим точки окрестности Vd (M 0), для которых х=х 0. На этом множестве точек, функция f (x; y) становится функцией f (x 0; y) одной переменной у. Из (1) следует, что f (x 0; y)£ f (х 0; y 0) Замечание. Если функция z = f (x; y) дифференцируема в точке (х 0; y 0), то условие Следствие. Если функция z = f (x; y) имеет экстремум в точке (х 0; y 0) и дифференцируема этой точке, то df (х 0; y 0)=0. Определение 3. Точки, в которых частные производные равны нулю, называются стационарными точками функции z = f (x; y). Определение 4. Точки, в которых частные производные равны нулю (или не существуют) называются критическими точками функции z = f (x; y). Из теоремы 1 и определения 3 следует, что если функция дифференцируема, то точки экстремума являются стационарными точками. Обратное неверно. Не всякая стационарная точка является точкой экстремума. Пример. D Рассмотрим функцию z=f (x; y)= x 2 -y 2, f (0;0)=0.
Рассмотрим Теорема 2 (достаточное условие экстремума). Пусть функция z = f (x; y) определена иимеет непрерывные частные производные до второго порядка включительно в некоторой окрестности точки М 0(x 0; y 0) V (x 0; y 0). Пусть М 0(x 0; y 0) - стационарная точка, то есть
Тогда 1) если 2) если 3) если Доказательство.
Т.к. М 0(x 0; y 0) - стационарная точка, то df (x 0; y 0)=0, следовательно,
где D х = х-х 0, D у = y-y 0. Положим
Положим Тогда
1) Пусть В этом случае АС >0, следовательно, А ¹0, и первый трехчлен в скобках в формуле (2) можно записать следующим образом:
Очевидно, что при
Теперь рассмотрим второй трехчлен в (2). Если выбрать r достаточно малым (а, значит, и D х, D у малы), то, поскольку a, b, g ®0 при D х,D у ®0, будем иметь
Но тогда все выражение в скобках в (2) будет сохранять тот же знак, что и первый трехчлен, то есть знак коэффициента А. Итак, если A >0, то и D f (x 0; y 0)>0. Следовательно, f (x; y)> f (x 0; y 0). Т.е. в точке (x 0; y 0) функция имеет строгий минимум. А если A <0, то и D f (x 0; y 0)<0. Следовательно, f (x; y)< f (x 0; y 0). Значит, в точке (x 0; y 0) функция имеет строгий максимум. 2) Предположим теперь, что а) Пусть А ¹0. Тогда можно использовать преобразование (3). Если j = j 1=0, то из (3) следует, что выражение в квадратных скобках равно Если j = j 2 определить так, что A cos j 2+ B sin j 2=0 (ясно, что при этом sin j 2¹0, т. к. иначе будет А =0), то выражение в квадратных скобках равно Если r достаточно мало, то второй трехчлен в скобках в (2) будет сколь угодно мал. Следовательно, знак D f определяется знаком первого трехчлена. Из (3) следует: при A >0 и j = j 1 он положителен, j = j 2 он отрицателен, при A <0 и j = j 1 он отрицателен, j = j 2 он положителен. Итак, в любой окрестности точки (х 0; y 0) D f будет иметь значения противоположных знаков на лучах j = j 1 и j = j 2. Следовательно, точка (х 0; y 0) не может быть точкой экстремума. б) Пусть А =0. Тогда первый трехчлен в (2) равен
Если А =0, то из условия Теорема 2 равносильна следующей теореме. Теорема 3. Пусть df (х 0; y 0)=0. Если d 2 f (х; y) сохраняет знак в некоторой достаточно малой окрестности точки (х 0; y 0), то в этой точке функция имеет строгий экстремум, причем, если d 2 f (х 0; y 0)<0, то строгий максимум, а если d 2 f (х 0; y 0)>0, то строгий минимум. В таком виде достаточное условие экстремума переносится на случай функций любого числа переменных. Пример. Исследовать функцию f (x; y)= xy (a-x-y), a >0 на экстремум.
 . .
Найдем стационарные точки. f¢x = y (a-x-y) -xy = y (a- 2 x-y), f¢y = x (a-x-y) -xy = x (a-x- 2 y)
Стационарные точки: О (0;0), М (а;0), N (0;a), Проверим, являются ли они точками экстремума.
О (0;0): А =0, В=а, С =0, АС-В 2=0 -а 2<0 Þ экстремума нет; М (а;0): А =0, В=-а, С = - 2 а, АС-В 2=0 -а 2<0 Þ экстремума нет; N (0; a): А =-2 a, В=-а, С =0, АС-В 2=0 -а 2<0 Þ экстремума нет;
2. Экстремум неявно заданной функции
 дважды непрерывно дифференцируема в дважды непрерывно дифференцируема в  . Если (х 0; у 0) – стационарная точка, то в ней выполнены равенства: . Если (х 0; у 0) – стационарная точка, то в ней выполнены равенства:
Очевидно, верно и обратное утверждение. Следовательно, стационарные точки неявной функции могут быть найдены из системы:
Достаточное условие формулируется так же, как в случае явного задания функции.
3. Нахождение наибольших и наименьших значений Пусть функция z = f (x; y) определена и дифференцируема на ограниченной замкнутой области G. Тогда она на имеет наибольшее и наименьшее значения. Если наибольшее (наименьшее) значение функция f принимает во внутренней точке области, то эта точка является точкой максимума (минимума). Т.о., ²подозрительными² точками внутри области являются стационарные точки. Но функция f может принимать наибольшее (наименьшее) значения и на границе области G. План нахождения наибольшего и наименьшего значений функции 1. Найти стационарные точки внутри области и значения функции в них. 2. Найти наибольшее и наименьшее значения на границе области и значения функции в них. Для этого границу области следует задать либо одним уравнением, либо параметрически. Тогда на границе исходная функция будет функцией одного переменного. 3. Если в области существуют точки, в которых функция не дифференцируема, то надо вычислить в них значения функции. 4. Из полученных чисел выбрать наибольшее и наименьшее. Пример. Найти наибольшее и наименьшее значения функции z=f (x; y)=2 x 2 - 2 y 2 в круге х 2+ у 2£9. D 1) z 1= f (0;0)=0. 2) Граница области задана уравнением х 2+ у 2=9. Отсюда у 2=9- х 2. Тогда на границе получаем функцию одной переменной: z= 2 x 2 - 2(9- х 2), z =4 х 2-18, x Î[-3;3]. z ¢=8 x, z ¢=0 при х =0. Тогда у =±3. Значения функции в стационарных точках границы: z 2= f (0;3)=-18, z 3= f (0;-3)=-18. Значения функции на концах отрезка [-3;3]: z 4= f (3;0)=18, z 5= f (-3;0)=18. 3) zнаиб. = f (3;0)= f (-3;0)=18, zнаим. = f (0;3)= f (0;-3)=-18. D
|

 , такая, что
, такая, что  выполнено неравенство f (x; y)< f (х 0; y 0) (f (x; y)> f (х 0; y 0)).
выполнено неравенство f (x; y)< f (х 0; y 0) (f (x; y)> f (х 0; y 0)). и
и  , то они в этой точке равны нулю, то есть
, то они в этой точке равны нулю, то есть  Пусть z = f (x; y) имеет в точке M 0(x 0; y 0) максимум. Тогда
Пусть z = f (x; y) имеет в точке M 0(x 0; y 0) максимум. Тогда  выполнено
выполнено , функция f (x; y) превращается в функцию f (x; y 0) одной переменной х. Из (1) следует, что f (x; y 0)£ f (х 0; y 0)
, функция f (x; y) превращается в функцию f (x; y 0) одной переменной х. Из (1) следует, что f (x; y 0)£ f (х 0; y 0)  . Это означает, что функция одной переменной f (x; y 0)имеет в точке х 0 максимум. По условию
. Это означает, что функция одной переменной f (x; y 0)имеет в точке х 0 максимум. По условию  . Она совпадает с
. Она совпадает с  в точке х 0, т.е
в точке х 0, т.е  .На основании необходимого условия экстремума функции одной переменной
.На основании необходимого условия экстремума функции одной переменной 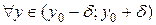 . Значит, функция одной переменной f (x 0; y)имеет в точке у 0 максимум.По необходимому условию экстремума функции одной переменной
. Значит, функция одной переменной f (x 0; y)имеет в точке у 0 максимум.По необходимому условию экстремума функции одной переменной  =0. Следовательно,
=0. Следовательно, 
 равносильно условию df (х 0; y 0)=0.
равносильно условию df (х 0; y 0)=0. ,
,  Þ (0;0) – стационарная точка.
Þ (0;0) – стационарная точка. . На оси О х f (x;0)= x 2>0, на оси О у f (0; y)= -y 2<0. Следовательно, в любой окрестности
. На оси О х f (x;0)= x 2>0, на оси О у f (0; y)= -y 2<0. Следовательно, в любой окрестности  и
и  . Обозначим
. Обозначим .
. то z = f (x; y) имеет в точке М 0(x 0; y 0) экстремум, причем при A <0 (C <0)- локальный максимум, при A >0 (C >0) - локальный минимум;
то z = f (x; y) имеет в точке М 0(x 0; y 0) экстремум, причем при A <0 (C <0)- локальный максимум, при A >0 (C >0) - локальный минимум; , то точка М 0(x 0; y 0) не является точкой экстремума;
, то точка М 0(x 0; y 0) не является точкой экстремума;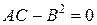 , то никакого заключения о характере стационарной точки сделать нельзя, требуются дополнительные исследования.
, то никакого заключения о характере стационарной точки сделать нельзя, требуются дополнительные исследования. (0< q <1).
(0< q <1).
 ,
, , где
, где 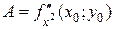 ,
,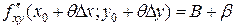 , где
, где  ,
, , где
, где 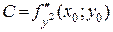 .
. Т.к. частные производные второго порядка непрерывны, то
Т.к. частные производные второго порядка непрерывны, то  . Полное приращение функции запишется в виде:
. Полное приращение функции запишется в виде:
 .
. , где
, где  .
.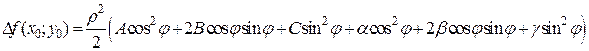 .(2)
.(2)

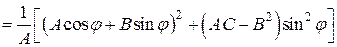 . (3)
. (3)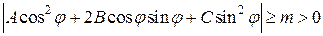 .
. .
. .
. .
. .
.







 .
. ,
,  ,
,  .
. ,
,  ,
,  ,
, Þ К – точка экстремума, т.к. A <0, то
Þ К – точка экстремума, т.к. A <0, то  ,
, 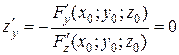 ,
, ,
,  .
.
 ,
,  Þ (0;0) – стационарная точка.
Þ (0;0) – стационарная точка.


