Примеры.
 , ,
  - однозначная функция от х. - однозначная функция от х.

 , то оно определяет однозначную функцию , то оно определяет однозначную функцию 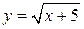 . .
3) Из примеров видно, что уравнение F (x; y)=0 не всегда определяет функцию y = f (x) (кроме того, далеко не всегда уравнение (1) можно разрешить относительно y). Поэтому необходимо знать условия существования неявной функции. Теорема 1. (достаточные условия существования и дифференцируемости неявной функции). Пусть дано уравнение F (x; y)=0 (1), и выполнены условия: 1) функция F (x; y) и ее частные производные 2) 3) Тогда справедливы следующие утверждения: а) в некотором прямоугольнике (x 0 -d, x 0+ d; y 0 -d¢;, y 0+ d¢;) уравнение (1) определяет неявную функцию y = f (x); б) f (x 0)= y 0; в) функция y = f (x) непрерывна в промежутке [ x 0 -d; x 0+ d ]; г) функция y = f (x) в промежутке [ x 0 -d; x 0+ d ] имеет непрерывную производную, причем Доказательство. а) (существование неявной функции y = f (x)) Согласно условию (3)
Пусть этой окрестностью является квадрат со сторонами 2 d¢; и центром в точке (x 0; y 0):[ x 0 -d¢;, x 0+ d¢;; y 0 -d¢;, y 0+ d¢;]. Будем передвигаться по вертикали А 0 В 0, проходящей через точку М 0, т. е. фиксируем х=х 0. Тогда рассматриваемая функция F (x; y) является функцией одной переменной у: F (x 0; y), у Î[ y 0 -d¢;, y 0+ d¢;]. В силу условия (2) эта функция возрастает. Т. к. при у = у 0 y 0 -d¢;< y 0 Þ F (x 0; y 0 -d¢;)< F (x 0; y 0)=0, y 0 +d¢;> y 0 Þ F (x 0; y 0 +d¢;)> F (x 0; y 0)=0.
F (x 0; y 0 +d¢;)>0. (4) Теперь будем двигаться по горизонтали, проходящей через точку А 0, т. е. фиксируем у = y 0 -d¢;. Получим функцию одной переменной х: F (x; y 0 -d¢;). Согласно (3) при х=х 0 эта функция принимает отрицательное значение. Т. к. по условию 1) теоремы функция F (x; y) непрерывна по совокупности переменных, то она непрерывна и по переменной х. Следовательно, в некоторой достаточно малой окрестности точки х 0 Аналогично, будем передвигаться по горизонтали, проходящей через точку В 0, т. е. фиксируем у = y 0 +d¢;. Т.к. F (x 0; y 0 +d¢;)>0 (по (4)), и функция F (x; y 0 +d¢;) непрерывна, то F (x; y 0 -d¢;)<0, F (x; y 0 +d¢;)>0. (5) Т. о., мы установили, что функция F (x; y) принимает отрицательные значения на горизонтали А 1 А 2 и положительные – на горизонтали В 1 В 2. Зафиксируем теперь произвольное б) По условию 2) в) (непрерывность неявной функции y = f (x)) Докажем непрерывность функции y = f (x) в точке х 0. Зафиксируем Пусть теперь г) (существование непрерывной производной функции y = f (x)) Придадим значению х приращение D х, неявная функция получит приращение D у. Т.к. F (x; y)=0 и F (x +D х; y +D у)=0, то и D F = F (x +D х; y +D у)- F (x; y)=0. (6) Преобразуем D F:
Здесь применили формулу Лагранжа к функции F (x; y +D у) на отрезке [ x; x +D х ] и к функции F (x; y) на отрезке [ у; у +D у ]. Из (6), (7) следует
Отсюда Пусть D х ®0. Т. к. y = f (x) непрерывная функция, то D у ®0. Т. к. Следовательно,
Мы доказали существование производной неявной функции и способ ее вычисления. Докажем непрерывность. Она следует из (9). По доказанному у = f (x) – непрерывная функция, по условию Замечание 1. Формулу (9) можно получить следующим образом. Продифференцируем равенство F (x;f (x))º0 по x (F – сложная функция от x):
Замечание 2. В уравнении (1) F (x;y)=0 переменные x и y равноправны. Следовательно, можно ставить вопрос о существовании функции Пример 1. Вычислить производные первого и второго порядка функции, заданной неявно уравнением D 1 способ вычисления
2 способ вычисления (*) Найдем
Далее надо преобразовать и подставить Второй способ вычисления 2. Уравнения касательной и нормали к кривой Пусть дано уравнение (1) F (x;y)=0, и для функции F (x;y) в окрестности точки (х 0; y 0) выполнены условия теоремы 1. Тогда в окрестности точки х 0 V (х 0) уравнение (1) задает функцию у = f (х), определенную, непрерывную и дифференцируемую в некоторой окрестности точки х 0 и f (х 0)= y 0. Графиком этой функции является некоторая кривая. Так как существует Для функции y = f (x) уравнение касательной точке х 0 имеет вид:
нормали: Из теоремы 1 следует Подставляя (12) в (10), (11), получим
3. Неявные функции нескольких переменных Пусть дано уравнение
 - функция (n +1)-й переменной. Если в каждой точке - функция (n +1)-й переменной. Если в каждой точке  существует единственное значение y, которое совместно с x удовлетворяет уравнению (13), то уравнение (13) на множестве G определяет функцию n переменных существует единственное значение y, которое совместно с x удовлетворяет уравнению (13), то уравнение (13) на множестве G определяет функцию n переменных  , (14) , (14)
и имеет место тождество Теорема 2 (достаточное условие существования и дифференцируемости неявной функции n переменных). Пусть функция F и ее частные производные
  . .
Рассмотрим частный случай. Пусть на F (x; y; z)=0. (15)
 , т.е. справедливо тождество (16) F (x; y; f (x; y)) , т.е. справедливо тождество (16) F (x; y; f (x; y))  0. Правая часть (16) – сложная функция от х и у. в силу условий теоремы (2) (существуют непрерывные 0. Правая часть (16) – сложная функция от х и у. в силу условий теоремы (2) (существуют непрерывные  ) эта функция дифференцируема на D. Дифференцируя (16) по x, получим: ) эта функция дифференцируема на D. Дифференцируя (16) по x, получим:
Отсюда Дифференцируя (16) по y, получим:
Отсюда Пример 2. Пусть уравнение D По формулам (17), (18):
Подставляя сюда выражение для Тогда
4. Уравнения касательной плоскости и нормали к поверхности Пусть уравнение (15) F (x; y; z)=0 определяет поверхность. Тогда (15) называется уравнением поверхности. Пусть в окрестности (x 0; y 0; z 0) выполняется условия теоремы 2. Тогда в окрестности точки (x 0; y 0) определена функция z = f (x; y), дифференцируемая в этой окрестности. Тогда поверхность z = f (x; y) имеет касательную плоскость и нормаль в точке (x 0; y 0).
Так как
уравнение касательной плоскости,
Неявные функции могут определяться системой функциональных уравнений.
|

 F (x; y)=
F (x; y)=  . Данное уравнение представляет двузначную функцию
. Данное уравнение представляет двузначную функцию  .
. не определяет функции y = f (x).
не определяет функции y = f (x).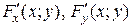 определены и непрерывны в некотором прямоугольнике [ x 0 -a, x 0+ a; y 0 -b, y 0+ b ];
определены и непрерывны в некотором прямоугольнике [ x 0 -a, x 0+ a; y 0 -b, y 0+ b ]; ;
; .
.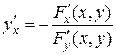 .
. . Предположим для определенности, что
. Предположим для определенности, что 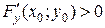 . Т. к. согласно условию (1)
. Т. к. согласно условию (1) 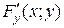 непрерывна, то в некоторой окрестности точки М 0(x 0; y 0) выполнено неравенство
непрерывна, то в некоторой окрестности точки М 0(x 0; y 0) выполнено неравенство (по условию 2) теоремы), то на концах отрезка [ y 0 -d¢;, y 0+ d¢;] она принимает значения разных знаков. Учитывая возрастание функции, получим:
(по условию 2) теоремы), то на концах отрезка [ y 0 -d¢;, y 0+ d¢;] она принимает значения разных знаков. Учитывая возрастание функции, получим: Итак, F (x 0; y 0 -d¢;)<0, (3)
Итак, F (x 0; y 0 -d¢;)<0, (3) выполнено F (x; y 0 -d¢;)<0.
выполнено F (x; y 0 -d¢;)<0. , такое, что в окрестности
, такое, что в окрестности  выполнено F (x; y 0 +d¢;)>0. Положим
выполнено F (x; y 0 +d¢;)>0. Положим  . Тогда для х: x 0 -d < x < x 0+ d имеем
. Тогда для х: x 0 -d < x < x 0+ d имеем ,
,  и будем изменять у от у 0 -d¢; до у 0 +d¢;, т. е. будем двигаться по АВ. При этом получаем функцию одной переменной у:
и будем изменять у от у 0 -d¢; до у 0 +d¢;, т. е. будем двигаться по АВ. При этом получаем функцию одной переменной у:  , которая непрерывна. Т. к. на концах отрезка [ у 0 -d¢;; у 0 +d¢;] она принимает значения разных знаков, то существует значение
, которая непрерывна. Т. к. на концах отрезка [ у 0 -d¢;; у 0 +d¢;] она принимает значения разных знаков, то существует значение  . Т. к. согласно (2) функция
. Т. к. согласно (2) функция  существует единственное значение
существует единственное значение  , которое вместе с х удовлетворяет уравнению (1). Следовательно, в прямоугольнике (x 0 -d, x 0+ d; y 0 -d¢;, y 0+ d¢;) уравнение (1) определяет у как неявную функцию от х. Обозначим ее y = f (x).
, которое вместе с х удовлетворяет уравнению (1). Следовательно, в прямоугольнике (x 0 -d, x 0+ d; y 0 -d¢;, y 0+ d¢;) уравнение (1) определяет у как неявную функцию от х. Обозначим ее y = f (x).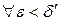 . Тогда, рассуждая, как и в пункте а), для этого e найдем
. Тогда, рассуждая, как и в пункте а), для этого e найдем  соответствующее ему единственное значение y = f (x), которое вместе с этим х удовлетворяет условию (1), окажется между
соответствующее ему единственное значение y = f (x), которое вместе с этим х удовлетворяет условию (1), окажется между  и
и 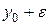 . То есть
. То есть  выполнено
выполнено  . По определению это означает, что функция y = f (x) непрерывна в точке х 0.
. По определению это означает, что функция y = f (x) непрерывна в точке х 0.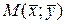 , где
, где  , удовлетворяет тем же условиям, что и точка М 0(x 0; y 0), т. к.
, удовлетворяет тем же условиям, что и точка М 0(x 0; y 0), т. к.  . Поэтому, как и выше, в некоторой окрестности точки
. Поэтому, как и выше, в некоторой окрестности точки  . Но именно ввиду однозначности эта функция совпадает с f (x). Следовательно, функция y = f (x) непрерывна в точке
. Но именно ввиду однозначности эта функция совпадает с f (x). Следовательно, функция y = f (x) непрерывна в точке 
 , где
, где  . (7)
. (7) .
. . (8)
. (8)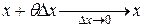 ,
,  ,
, 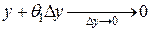 , и
, и  ,
,  - непрерывные функции, то
- непрерывные функции, то  ,
, 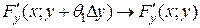 .
. правой части равенства (8), равный
правой части равенства (8), равный  . Значит,
. Значит,  . Переходя в (8) к пределу, получим
. Переходя в (8) к пределу, получим . (9)
. (9) - непрерывные функции от х и у. Следовательно, сложные функции от х
- непрерывные функции от х и у. Следовательно, сложные функции от х  и
и  непрерывны. В силу условия 3) знаменатель в (9) не равен нулю. Из всего сказанного следует, что
непрерывны. В силу условия 3) знаменатель в (9) не равен нулю. Из всего сказанного следует, что  - непрерывная функция.
- непрерывная функция. 
 ,
, Þ (9)
Þ (9) . В этом случае в теореме (1) надо изменить условие 3) – требовать, чтобы
. В этом случае в теореме (1) надо изменить условие 3) – требовать, чтобы  . Но если одновременно
. Но если одновременно 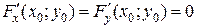 , то нельзя утверждать, что уравнение (1) определяет какую-либо неявную функцию.
, то нельзя утверждать, что уравнение (1) определяет какую-либо неявную функцию. (x >0).
(x >0). .
. .
. ,
,  .
. , учитывая, что у = у (х), а х – независимая переменная:
, учитывая, что у = у (х), а х – независимая переменная: .
. , то существует касательная и нормаль к кривой (1).
, то существует касательная и нормаль к кривой (1). , (10)
, (10) . (11)
. (11) . (12)
. (12) Þ
Þ – уравнение касательной;
– уравнение касательной; или
или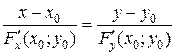 – уравнение нормали.
– уравнение нормали. . (13)
. (13) на G.
на G. непрерывны в некоторой окрестности точки
непрерывны в некоторой окрестности точки  , и пусть
, и пусть  , а
, а  . Тогда уравнение (13) определяет функцию
. Тогда уравнение (13) определяет функцию  , а частные производные
, а частные производные 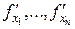 находятся по формулам:
находятся по формулам: дано уравнение
дано уравнение .
. . (17)
. (17) .
. . (18)
. (18)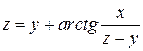 определяет функцию z = f (x; y). Найти
определяет функцию z = f (x; y). Найти 
 .
.

 ,
, ,
,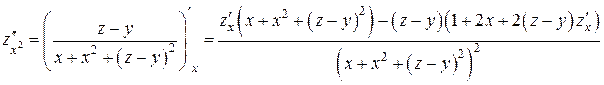 .
. и заменяя z на f (x; y), найдем
и заменяя z на f (x; y), найдем  .
. . D
. D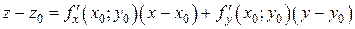 – уравнение касательной плоскости,
– уравнение касательной плоскости, – уравнение нормали.
– уравнение нормали. , то
, то –
– – уравнение нормали.
– уравнение нормали.


