Функции нескольких переменных
1. Понятие частных производных
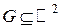 , (х 0, у 0) – внутренняя точка множества G. , (х 0, у 0) – внутренняя точка множества G.
Определение. Если существует конечный предел
то он называется частной производной функции z = f (x, y) по переменной х в точке (х 0, у 0) и обозначается Если существует конечный предел
то он называется частной производной функции z = f (x, y) по переменной у в точке (х 0, у 0) и обозначается Итак, Из определения следует, что частная производная функции z = f (x, y) по переменной х в точке (х 0, у 0) является обычной производной функции одной переменной f (х, у 0) в точке х 0. Если функция z = f (x, y) имеет частную производную Пример 1. Найти частные производные функции
 D D  . .
Аналогично определяются частные производные функции трех и большего числа переменных.
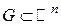 , , 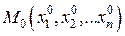 - внутренняя точка множества G. - внутренняя точка множества G.
Определение. Если существует конечный предел
то он называется частной производной функции u = f (x 1, x 2,… xn) по переменной xj в точке
Геометрический смысл частных производных
 Пусть функция z = f (x, y) определена на множестве Пусть функция z = f (x, y) определена на множестве 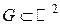 . Рассмотрим поверхность z = f (x, y), являющуюся графиком этой функции. Пусть точка M 0(x 0, y 0, z 0) принадлежит поверхности. Проведем через точку M 0 плоскость x = x 0, параллельную плоскости y O z. Кривая z = f (x 0, y) является линией пересечения поверхности и плоскости. Частная производная данной функции по переменной у совпадает с производной функции f (x 0, y) в точке у = у 0: . Рассмотрим поверхность z = f (x, y), являющуюся графиком этой функции. Пусть точка M 0(x 0, y 0, z 0) принадлежит поверхности. Проведем через точку M 0 плоскость x = x 0, параллельную плоскости y O z. Кривая z = f (x 0, y) является линией пересечения поверхности и плоскости. Частная производная данной функции по переменной у совпадает с производной функции f (x 0, y) в точке у = у 0:
Следовательно,
2. Дифференцируемость и дифференциал функции нескольких переменных
Пусть функция z = f (x, y) определена на множестве Пример 2. Найти полное приращение функции z = x 2 -xy + y 2 в точке (х 0, у 0).
Если координатам фиксированной точки (х 0, у 0) придают фиксированные приращения, то D z –число. Если фиксируется только точка (х 0, у 0), то D z =D z (D x,D y) - функция переменных D x и D y. Если ничего не фиксируется, то D z =D z (х 0, у 0,D x,D y)– функция четырех переменных. В примере D z можно представить в виде D z = А D х + В D у + a D х + b D у, где Но не для каждой функции двух переменных ее полное приращение можно представить таким образом.
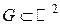 . Функция f (x, y) называется дифференцируемой в точке (х 0, у 0)Î G, если ее полное приращение в этой точке можно представить в виде . Функция f (x, y) называется дифференцируемой в точке (х 0, у 0)Î G, если ее полное приращение в этой точке можно представить в виде
D z = А D х + В D у + a D х + b D у, (1) где А, В - постоянные, a=a (D x,D y), b=b (D x,D y)- бесконечно малые функции при D х ®0, D у ®0. Полное приращение дифференцируемой функции можно записать также в виде: D z = А D х + В D у + e × r, (2) где Покажем, что (1) эквивалентно (2). 1) (1)Þ(2). Т. к. первые два слагаемых одинаковые, то надо показать, что a D х + b D у можно представить в виде e × r (с выполнением соответствующих условий).
т.к. Пусть 2) (2)Þ(1). где
Пусть D x ®0, D y ®0. Тогда r ®0. Отсюда, по условию, e ®0. А, значит, в силу неравенств (**), a ®0, b ®0. Итак, условия (1) и (2) эквивалентны. Замечание. Т.к. D z = А D х + В D у + o (r). (3) Определение. Пусть функция z = f (x, y) дифференцируема в точке (х 0, у 0). Дифференциалом функции f в точке (х 0, у 0). Называется линейная относительно D x и D y часть полного приращения функции в точке (х 0, у 0). Обозначается dz, df (х 0, у 0). dz = А D х + В D у. (4) Т.о., D z = dz + a D х + b D у или D z = dz + o (r). (5) Т.к. D z-dz = o (r), то D z и dz одного порядка малости при r ®0. Из (5) также следует, что dz ¹0 – главная часть полного приращения функции при r ®0. Т.о., дифференциал обладает двумя свойствами: 1) является линейной частью приращения функции; 2) если dz ¹0, то он является главной частью полного приращения при r ®0. Из второго свойства следует применение дифференциала к приближенным вычислениям: D f (х 0, у 0)» df (х 0, у 0) при r ®0, f (х 0+D х, у 0+D у)= f (х, у)» f (х 0, у 0)+ df (х 0, у 0). Теорема 1 (непрерывность дифференцируемой функции). Если функция z = f (x, y) дифференцируема в точке (х 0, у 0), то она непрерывна в этой точке. Доказательство.
D z = А D х + В D у + a D х + b D у, где А, В - постоянные, Пусть D x ®0, D y ®0. Тогда a ®0, b ®0, и, значит, D f (х 0, у 0)®0. Т.е. бесконечно малым приращениям аргументов в точке (х 0, у 0) соответствует бесконечно малое полное приращение функции. Следовательно, по определению, функция z = f (x, y) непрерывна в точке (х 0, у 0). Теорема 2 (необходимое условие дифференцируемости). Если функция z = f (x, y) дифференцируема в точке (х 0, у 0), то в этой точке существуют конечные частные производные
т.е. всегда Доказательство.
Обозначим
Разделим обе части этого равенства на D х ¹0: Т.к. существует предел правой части при D х ®0:
Аналогично доказывается, что Замечание 1. Теорема, обратная к теореме 1, неверна. Функция, непрерывная в точке (х 0, у 0), может быть не дифференцируема в ней.
 , функция непрерывна на , функция непрерывна на 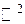 . .
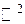 , кроме точек оси О у. , кроме точек оси О у.
Следовательно, " у Замечание 2. Теорема, обратная к теореме 2, не имеет места. Функция f (x, y), имеющая частные производные
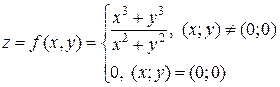 имеет в точке (0;0) частные производные, но не дифференцируема в этой точке. имеет в точке (0;0) частные производные, но не дифференцируема в этой точке.
D
Итак, частные производные существуют в точке (0;0). Докажем, что функция не дифференцируема в точке (0;0). От противного. Пусть функция дифференцируема в точке (0;0). Тогда
может быть представлено в виде:
Т.к.
Докажем, что этот предел не существует. Пусть D х ®0, D у ®0, так, что D у = k D x, k ¹0. Тогда
Предел зависит от k, значит, он не существует. Поэтому сделанное предположение неверно, и функция не дифференцируема в точке (0;0). D
Доказательство.
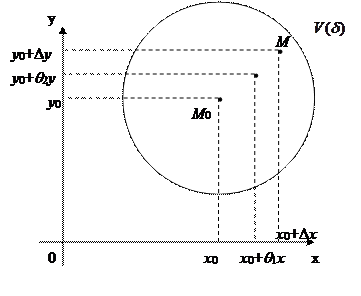
Придадим х 0, у 0 произвольные приращения D х и D у, не равные нулю одновременно и такие, чтобы
Первая скобка является частным приращением по переменной х функции f (x, y) в точке В силу условия функция
Подставим (8) и (9) в (7):
Добавим и вычтем справа
Обозначим
Тогда Пусть
Следовательно,
3. Выражение дифференциала через частные производные
 . Тогда в этой точке имеет место соотношение . Тогда в этой точке имеет место соотношение
и функция имеет дифференциал
Под дифференциалами независимых переменных понимают произвольные приращения этих переменных, т. е. dx =D x, dy =D y. Тогда Обозначим
dz = dxz + dyz. Очевидно, что дифференциал функции в точке (х 0; у 0) есть функция двух переменных D х и D у: df (х 0; у 0)= j (D x;D y). Если функция дифференцируема в каждой точке множества G, то говорят, что она дифференцируема на G. В этом случае f на G имеет дифференциал
и dz = j (x; y;D x;D y) – функция четырех переменных.
4. Касательная плоскость и нормаль к поверхности Напомним вначале понятие касательной к кривой.
Определение. Прямая М 0 Т называется касательной к кривой в точке М 0, если угол j между этой прямой и секущей стремится к нулю, когда r ®0, независимо от способа передвижения точки М по кривой к точке М 0. Аналогично вводится понятие касательной плоскости к поверхности.
Определение. Плоскость Q, проходящая через точку Р 0, принадлежащую поверхности, называется касательной плоскостью в этой точке, если угол j между этой плоскостью и секущей Р 0 Р стремится к 0, когда точка Р стремится к точке Р 0, т.е. r (Р 0; Р)®0. Определение. Нормалью к поверхности в точке Р 0 на ней называется прямая, проходящая через точку Р 0 и перпендикулярная касательной плоскости в этой точке. На рисунке P 0 N – нормаль. Теорема 4. Если функция z = f (x; y) дифференцируема в точке (х 0; у 0), то в точке P 0(x 0; y 0; z 0), где z 0= f (x 0; y 0) существуют касательная плоскость и нормаль к поверхности z = f (x; y). Уравнение касательной плоскости имеет вид
Нормаль задается уравнением:
Доказательство.
где
Из курса аналитической геометрии известно, что это уравнение определяет в декартовой системе координат плоскость, проходящую через точку P 0(x 0; y 0; z 0) и имеющую нормальный вектор 1) плоскость Q проходит через точку Р 0 поверхности; 2) угол j между нормальным вектором 1) очевидно. Докажем 2). Вычислим косинус угла j между векторами
Þ Из (13) следует, что
Значит, Т.о., касательная плоскость к поверхности z = f (x; y) в точке (x 0; y 0; z 0) задается уравнением (11), а условие дифференцируемости функции в точке (x 0; y 0) с геометрической точки зрения означает существование касательной плоскости к графику функции z = f (x; y) в точке P 0(x 0; y 0; z 0). Напомним, что уравнение прямой, проходящей через точку P 0(x 0; y 0; z 0) и имеющей направляющий вектор
Так как направляющим вектором нормали является вектор
5. Геометрический смысл дифференциала Пусть функция z = f (x; y) дифференцируема в точке (х 0; у 0). Тогда в этой точке существует дифференциал
KP = MP – МК = MP – M 0 P 0= z–z 0=∆ z. ∆ z – приращение аппликаты на поверхности в точке Р 0, соответствующее приращениям ∆ x, ∆ y абсциссы и ординаты. KL = ML – MK = ML – M 0 P 0= ML – z 0.(*) Из уравнения касательной плоскости ML = z 0+ dz. Отсюда dz = ML – z 0. (**) Из соотношений (*) и (**) следует, что KL = dz. Следовательно, дифференциал функции в точке M 0(x 0, y 0) численно равен приращению КL аппликаты точки Р 0 на касательной плоскости, соответствующему приращению аргументов ∆ x и ∆ y.
|

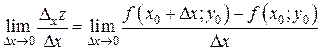 ,
, ,
,  ,
,  ,
, 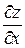 .
.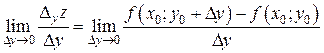 ,
,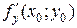 ,
, 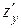 ,
, 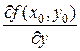 ,
, 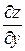 .
. ,
, 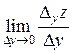 .
. в каждой точке (х, у)Î G, то говорят, что частная производная существует на G. В этом случае каждой точке (х, у)Î G соответствует число
в каждой точке (х, у)Î G, то говорят, что частная производная существует на G. В этом случае каждой точке (х, у)Î G соответствует число 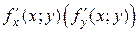 . Этим на множестве G определяются две функции, которые обозначаются
. Этим на множестве G определяются две функции, которые обозначаются  и
и 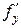 , и называются частными производными функции f на множестве G. Т.к. частная производная
, и называются частными производными функции f на множестве G. Т.к. частная производная 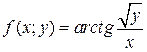 .
. ,
,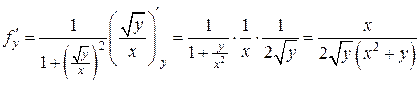 .
.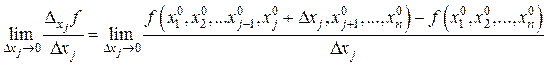
 ,
,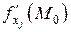 ,
, 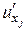 ,
, 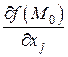 ,
,  .
. .
.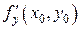 равна угловому коэффициенту касательной к кривой z = f (x 0, y) в точке M 0(x 0, y 0, z 0).
равна угловому коэффициенту касательной к кривой z = f (x 0, y) в точке M 0(x 0, y 0, z 0). 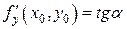 , где a - угол между касательной и положительным направлением оси О у.
, где a - угол между касательной и положительным направлением оси О у.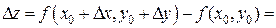



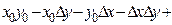

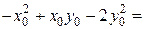
 .
.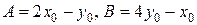 - постоянные,
- постоянные, 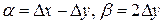 - функции от D x,D y, такие, что
- функции от D x,D y, такие, что 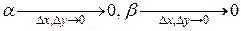 .
. ,
,  .
. , где
, где 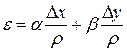 .
.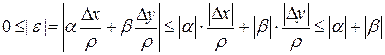 , (*)
, (*)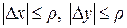 . Лекция 2 (1с)
. Лекция 2 (1с) , тогда D x ®0, D y ®0. Значит, по условию, a ®0, b ®0. Следовательно, в силу неравенства (*), e ®0. Итак, e ®0 при r ®0.
, тогда D x ®0, D y ®0. Значит, по условию, a ®0, b ®0. Следовательно, в силу неравенства (*), e ®0. Итак, e ®0 при r ®0. ,
,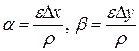 .
.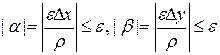 . (**)
. (**) Пусть функция z = f (x, y) дифференцируема в точке (х 0, у 0). Тогда ее полное приращение может быть представлено в виде (1)
Пусть функция z = f (x, y) дифференцируема в точке (х 0, у 0). Тогда ее полное приращение может быть представлено в виде (1)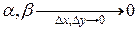 .
.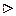
 ,
,  , (6)
, (6)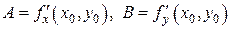 .
. .
. ,
,  . Тогда
. Тогда .
.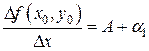 .
. , то существует и предел левой части:
, то существует и предел левой части: 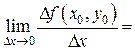
 Пример 3. z = f (x, y)=| x |.
Пример 3. z = f (x, y)=| x |.
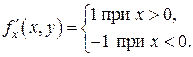
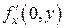 не существует. Из теоремы 2 следует, что функция не дифференцируема на оси О у. D
не существует. Из теоремы 2 следует, что функция не дифференцируема на оси О у. D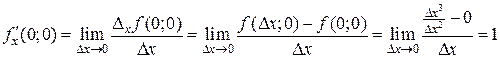 ,
, .
.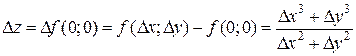
 , где
, где 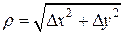 .
. , то
, то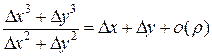
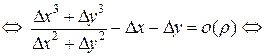

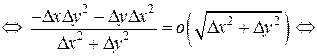

 .
. .
. Теорема 3 (достаточное условие дифференцируемости функции двух переменных). Пусть функция f (x, y) в некоторой окрестности точки (х 0, у 0) имеет частные производные
Теорема 3 (достаточное условие дифференцируемости функции двух переменных). Пусть функция f (x, y) в некоторой окрестности точки (х 0, у 0) имеет частные производные  .
. . Тогда функция f получит приращение
. Тогда функция f получит приращение  , которое можно представить в виде:
, которое можно представить в виде: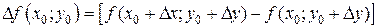
 (7)
(7)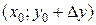 ; вторая скобка является частным приращением функции f (x, y) по переменной у в точке (х 0, у 0). Т. к. первая скобка является приращением функции одной переменной
; вторая скобка является частным приращением функции f (x, y) по переменной у в точке (х 0, у 0). Т. к. первая скобка является приращением функции одной переменной 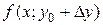 в точке х 0, а вторая - приращением функции одной переменной
в точке х 0, а вторая - приращением функции одной переменной  в точке у 0, то к ним можно применить теорему Лагранжа.
в точке у 0, то к ним можно применить теорему Лагранжа. имеет производную на
имеет производную на  , а функция
, а функция  .Тогда применяя теорему Лагранжа, получим
.Тогда применяя теорему Лагранжа, получим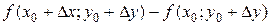 =
=  , (8)
, (8)

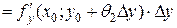 ,
,  . (9)
. (9)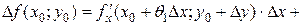
 ,
,  .
. и
и  :
: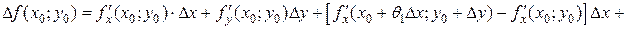
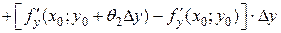 . (10)
. (10) ,
, 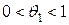 ,
,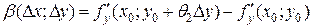 ,
,  . Если доказать, что
. Если доказать, что 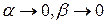 при
при 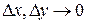 , то функция f (x, y) будет дифференцируема в точке (х 0, у 0) по определению.
, то функция f (x, y) будет дифференцируема в точке (х 0, у 0) по определению. . Так как
. Так как 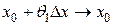 ,
,  ,
, 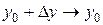 . Тогда в силу непрерывности частных производных в точке (х 0, у 0)
. Тогда в силу непрерывности частных производных в точке (х 0, у 0)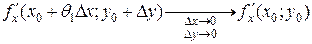 ,
, 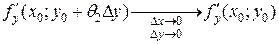 .
.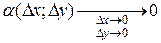 ,
, 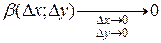 . По определению функция f (x, y) дифференцируема в точке (х 0, у 0).
. По определению функция f (x, y) дифференцируема в точке (х 0, у 0).  ,
, .
.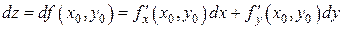 .
. - частный дифференциал функции по переменной х,
- частный дифференциал функции по переменной х, 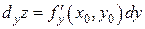 - частный дифференциал функции по переменной у. Тогда
- частный дифференциал функции по переменной у. Тогда , (х, у)Î G,
, (х, у)Î G, Пусть дана кривая и точка М 0 на ней. Возьмем произвольную точку М, принадлежащую кривой, и проведем секущую М 0 М. Пусть r = r (М 0; М).
Пусть дана кривая и точка М 0 на ней. Возьмем произвольную точку М, принадлежащую кривой, и проведем секущую М 0 М. Пусть r = r (М 0; М). Пусть точка Р 0 принадлежит поверхности, Р – произвольная точка поверхности. Проведем секущую Р 0 Р, r = r (Р 0; Р). Рассмотрим плоскость Q: P 0Î Q.
Пусть точка Р 0 принадлежит поверхности, Р – произвольная точка поверхности. Проведем секущую Р 0 Р, r = r (Р 0; Р). Рассмотрим плоскость Q: P 0Î Q.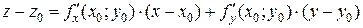 , (11)
, (11) . (12)
. (12) , (13)
, (13) ,
, 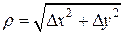 . Рассмотрим уравнение
. Рассмотрим уравнение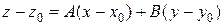 или
или  .
.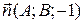 . Докажем, что эта плоскость Q является касательной в точке Р 0 к поверхности. Для этого достаточно показать, что
. Докажем, что эта плоскость Q является касательной в точке Р 0 к поверхности. Для этого достаточно показать, что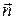 к этой плоскости и любой секущей Р 0 Р стремится к
к этой плоскости и любой секущей Р 0 Р стремится к 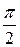 , когда точка Р, принадлежащая поверхности, стремится к точке Р 0, т.е. когда r ®0.
, когда точка Р, принадлежащая поверхности, стремится к точке Р 0, т.е. когда r ®0.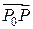 .
. ,
, 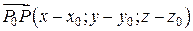 ,
,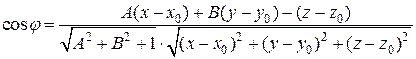 .
.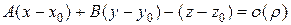 . Следовательно,
. Следовательно, .
. Þ
Þ  , и, следовательно, 2) доказано.
, и, следовательно, 2) доказано. , имеет вид
, имеет вид .
. , то уравнение нормали:
, то уравнение нормали: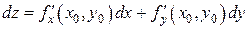 , а график функции в точке (x 0; y 0; z 0) имеет касательную плоскость, задаваемую уравнением (11).
, а график функции в точке (x 0; y 0; z 0) имеет касательную плоскость, задаваемую уравнением (11). Р 0 – точка касания, Q – касательная плоскость, т. L Î Q, [ P 0 L ]Î Q,
Р 0 – точка касания, Q – касательная плоскость, т. L Î Q, [ P 0 L ]Î Q,  принадлежит поверхности z = f (x; y). P 0 K ║ М 0 М, М 0 – проекция точки Р 0 на х O у.
принадлежит поверхности z = f (x; y). P 0 K ║ М 0 М, М 0 – проекция точки Р 0 на х O у.


