Предел и непрерывность функции двух переменных
1. Понятие предела функции двух переменных Пусть функция z = f (x, y) определена на множестве G Í Rn. Пусть М 0(х 0, у 0) – предельная точка множества G. Определение 1 (по Коши). Число А называется пределом функции f (x, y) в точке М 0(х 0, у 0), если " e >0 $ d = d (e)>0: " M (x, y)Î G: 0< r (M 0, M)< d выполнено неравенство | f (x, y) -A |< e. Обозначается Напомним, что в R2
 , таких что , таких что  выполнено выполнено  . .
Равносильность этих определений доказывается аналогично случаю функции одной действительной переменной. Аналогично вводится понятие предела функции n действительных переменных. Для предела функции n переменных справедливы все свойства предела функции одной переменной. Пример 1. Вычислить D Т. к. функции 3 ху и х 2 у являются бесконечно малыми при х ®1, у ®0, то tg3 xy ~3 xy, sin x 2 y ~ x 2 y. Тогда
 не имеет предела в точке О(0;0). не имеет предела в точке О(0;0).
D 1 способ. Пусть М (х; у)®О(0;0) по прямой у = kx, проходящей через точку О. Тогда
Т.о., приближаясь к точке О(0;0) по различным прямым, соответствующим различным значениям k, получаем, что функция стремится к различным значениям. Например, при k =0, т.е. приближаясь к точке О(0;0) по оси О х 2 способ. Рассмотрим две различные последовательности точек, стремящиеся к О(0;0). Первая последовательность Вторая последовательность
Т.о., двум различным последовательностям точек, стремящимся к О(0;0) по разным направлениям, соответствуют две последовательности значений функции, имеющие разные пределы. Согласно определению предела функции по Гейне это означает, что функция не имеет предела в точке (0;0).D Пример 3. Найти D Перейдем к полярным координатам с центром в точке О(0;0):
т.к. функция
2. Повторные пределы Для функций нескольких переменных наряду с обычным понятием предела функции (при одновременном стремлении всех аргументов к их пределам) вводится понятие повторного предела, получаемого в результате ряда последовательных предельных переходов по каждому аргументу в отдельности в том или ином порядке. (Обычный предел функции n переменных называется n -кратным: двойным, тройным и т.д.) Рассмотрим случай функции двух переменных. Пусть функция определена в области G. Пусть область G такова, что х может принимать (независимо от у) любые значения в некотором множестве Х, для которого х 0 – предельная точка, а переменная у (независимо от х) изменяется на множестве Y. Тогда G можно символически обозначить G = X ´ Y. При фиксированном значении переменной у функция f (x; y) становится функцией одной переменной х. Если при фиксированном y Î Y существует
При этом Другой повторный предел
получится, если предельные переходы произвести в обратном порядке. В (2) внутренний предел - Повторные пределы (1) и (2) вовсе не обязательно равны. Пример 4. Вычислить повторные пределы функции D О(0;0)Ï D (f), является предельной точкой D (f).
Может случиться, что один из повторных пределов существует, а другой – нет. Пример 5. Вычислить повторные пределы функции D
Всякая перестановка двух предельных переходов по разным переменным должна быть обоснована. Одно из таких обоснований дает следующая теорема. Она также устанавливает связь между двойными и повторными пределами. Вообще говоря, из существования двойного предела не следует существование повторных пределов, и из существования повторных не следует существование двойного. Теорема. Пусть в точке (х 0; у 0) существует (конечный или бесконечный) двойной предел Если $ Замечание. Обратное утверждение неверно. Если существуют и равны оба повторных предела, то двойной не обязательно существует. Пример 6. D
но
3. Непрерывность функции n переменных Определение 1. Функция z = f (x, y) называется непрерывной в точке M 0(x 0; y 0), если она определена в некоторой окрестности этой точки, и предел функции равен значению функции в этой точке:
Аналогично определяется непрерывность в точке функции n переменных. Обозначим х = х 0+D х, у = у 0+D у. Тогда (1) можно переписать с. о.:
Величина Определение 2. Функция z = f (x, y) называется непрерывной в точке M 0(x 0; y 0), если бесконечно малым приращениям аргументов х и у соответствует бесконечно малое полное приращение функции: Если переменную у 0 оставить постоянной, а переменной х 0 придать некоторое приращение D х, то функция z = f (x, y) получит приращение Для функций нескольких переменных вводится понятие непрерывности по каждой из независимых переменных. Определение. Частным приращением функции u = f (x 1, x 2,… xn) в точке
Определение. Функция u = f (x 1, x 2,…, xn) называется непрерывной в точке М 0 по переменной xj
Пример 7. Доказать, что функция непрерывна в точке О(0;0) по каждой переменной х и у, но не является непрерывной по совокупности переменных. D Частное приращение функции по переменной х в точке О(0;0):
Следовательно, функция непрерывна в т. О(0;0) по переменной х. Частное приращение функции по переменной у в точке О(0;0):
Следовательно, функция непрерывна в т. О(0;0) по переменной у. Но функция не является непрерывной в т.О(0;0) по совокупности переменных, т.к. предел функции в этой точке не существует (см. пример 2 из п.2). D Определение. Функция называется непрерывной на множестве, если она непрерывна в каждой точке этого множества. Определение. Точка M 0(x 0; y 0), в которой не выполняется условие непрерывности, называется точкой разрыва функции z = f (x; y). Это может быть, например, в следующих случаях: 1. z = f (x; y) определена во всех точках некоторой окрестности точки М 0, кроме самой точки М 0; 2. функция определена во всех точках V (М 0), но 3. функция определена во всех точках V (М 0), и существует Пример 2. Найти точки разрыва функции D Функция может иметь разрыв лишь в точках, где Итак, данная функция имеет разрыв на прямых у = х, у = -х, х =2. D
|

 или
или 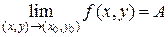 .
. .
. .
. .
.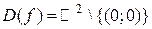 . Т.о., (0;0) – предельная точка D (f). Покажем, что
. Т.о., (0;0) – предельная точка D (f). Покажем, что  не существует.
не существует. .
. и т.д. Следовательно,
и т.д. Следовательно, 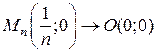 по положительной части оси О х. Тогда
по положительной части оси О х. Тогда  .
.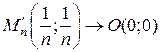 по направлению биссектрисы первого координатного угла (по прямой у=х). Тогда
по направлению биссектрисы первого координатного угла (по прямой у=х). Тогда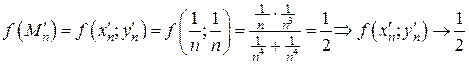 .
. .
. ,
, - бесконечно малаяпри r ®¥, а функция (cos j +sin j) ограничена.D
- бесконечно малаяпри r ®¥, а функция (cos j +sin j) ограничена.D , то, вообще говоря, этот предел зависит от наперед зафиксированного у:
, то, вообще говоря, этот предел зависит от наперед зафиксированного у:  . Теперь можно рассматривать
. Теперь можно рассматривать  . Пусть он существует и равен А:
. Пусть он существует и равен А:  . (1)
. (1) называется внутренним пределом в повторном пределе (1).
называется внутренним пределом в повторном пределе (1). (2)
(2) .
. в точке О(0;0).
в точке О(0;0). ,
, . D
. D в О(0;0).
в О(0;0). - не существует,
- не существует, . D
. D . Тогда существует повторный предел
. Тогда существует повторный предел  , то существует повторный предел
, то существует повторный предел 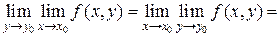
 ,
, ,
, не существует (см. пример 2). D
не существует (см. пример 2). D . (1)
. (1) или
или 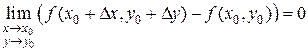 .
. называется полным приращением функции z = f (x, y) в точке (x 0; y 0). Т. о., получаем эквивалентное определение непрерывности функции в точке.
называется полным приращением функции z = f (x, y) в точке (x 0; y 0). Т. о., получаем эквивалентное определение непрерывности функции в точке. .
. , которое называется частным приращением функции z в точке (х 0, у 0) по переменной х. Аналогично, если переменная х 0 остается постоянной, а у 0 получает приращение D у, то
, которое называется частным приращением функции z в точке (х 0, у 0) по переменной х. Аналогично, если переменная х 0 остается постоянной, а у 0 получает приращение D у, то  - частное приращение функции z в точке (х 0, у 0) по переменной у.
- частное приращение функции z в точке (х 0, у 0) по переменной у.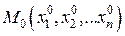 по переменной xj называется величина
по переменной xj называется величина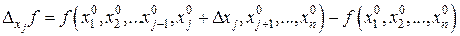 .
. , если
, если .
.

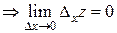 .
.
 .
.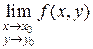 не существует;
не существует; .
. .
. =0 Û
=0 Û 



