Понятие функции нескольких переменных
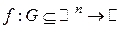 называется действительной функцией n действительных переменных. называется действительной функцией n действительных переменных.
Обозначается Множество G называется областью определения функции, а множество значений, которые принимает u – множеством значений функции f.
Пример. Найти область определения функции D D (z):
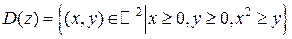 . D . D
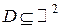 . Функция f задается множеством точек . Функция f задается множеством точек 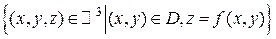 . Значит, это множество можно изобразить в трехмерном координатном пространстве. Получим множество точек, которое называется графиком функции z = f (x, y). Часто (но не обязательно) графиком такой функции является поверхность. Не каждая поверхность может быть графиком функции двух переменных. Если поверхность является графиком функции двух переменных, то любая прямая, параллельная оси О z пересекает ее не более, чем в одной точке. . Значит, это множество можно изобразить в трехмерном координатном пространстве. Получим множество точек, которое называется графиком функции z = f (x, y). Часто (но не обязательно) графиком такой функции является поверхность. Не каждая поверхность может быть графиком функции двух переменных. Если поверхность является графиком функции двух переменных, то любая прямая, параллельная оси О z пересекает ее не более, чем в одной точке.
Пример. D Рассмотрим функцию
Пусть функция z = f (x, y) задана на D Í Rn. Пересечем график функции плоскостью z = a. В сечении получим линию
Спроектируем ортогонально эту линию на плоскость х О у. Линия f (x, y)= a лежит в D и называется линией уровня функции f.
Придавая а разные значения, будем получать различные линии уровня. Значит, если а – параметр, то f (x, y)= a – семейство линий уровня. Обычно в качестве а берут числа а 1, а 2, а 3,…, образующие арифметическую прогрессию. В этом случае линии уровня дают некоторое наглядное представление о графике функции z = f (x, y). В тех местах, где линии уровня сгущены, функция возрастает быстрее, чем в тех местах, где они разрежены. Аналогично вводится понятие поверхностей уровня функции трех переменных u = f (x, y, z):
|

 .
. В случае n =2 обычно пишут z = f (x, y), а при n =3 u = f (x, y, z).
В случае n =2 обычно пишут z = f (x, y), а при n =3 u = f (x, y, z).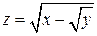 .
.
 .
.
 - круг с центром в (0;0), радиусом R =2.
- круг с центром в (0;0), радиусом R =2.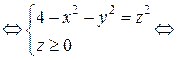
 - верхняя полусфера с центром в (0;0;0), радиусом R =2. D
- верхняя полусфера с центром в (0;0;0), радиусом R =2. D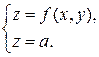
 Определение. Линией уровня функции z = f (x, y) называется множество точек (x, y) из области определения функции, в которых функция принимает одно и то же значение а.
Определение. Линией уровня функции z = f (x, y) называется множество точек (x, y) из области определения функции, в которых функция принимает одно и то же значение а. . Если а – параметр, то f (x, y, z)= а – семейство поверхностей уровня.
. Если а – параметр, то f (x, y, z)= а – семейство поверхностей уровня.


