Функций нескольких переменных
1. Обязанности снайперов………………………………………………..3 2. Материальная часть снайперской винтовки Драгунова (СВД)……10 3. Приёмы и правила стрельбы из СВД………………………………..15 4. Упражнения учебных стрельб из СВД ……………………………...21 5. Назначение и боевые свойства малокалиберной винтовки ТОЗ-18/01 с оптическим прицелом…………………………………………………..27 6. Приёмы и правила стрельбы из ТОЗ-18/01………………………….32 7. Упражнения стрельб из малокалиберной винтовки………………...36 8. Боеприпасы к СВД и малокалиберным винтовкам…………………40 9. Боевая работа снайперской пары…………………………………….40 10.Волевая настройка снайпера…………………………………………53 12.Первая помощь при ранениях………………………………………..54 13.Список литературы для самостоятельного изучения снайперами………………………………………………………………..55
Фролов Евгений Петрович
СПРАВОЧНИК СНАЙПЕРСКОЙ ПАРЫ Редактирование и корректоры: Усынина Е.Е. Компьютерная верстка: Овчинников М.В. _______
Лицензия ЛР № 021212 от 25.04.97 г.
______________________
Подписано в печать 25. 03.98 г. Формат 60х84/16 Усл.-печ.л. 3,5. Бумага писчая. Печать офсетная. Заказ № 472. Тираж 200 экз.
454081, г. Челябинск, ул. Лебединского, 41 Участок оперативной полиграфии Дифференциальное исчисление функций нескольких переменных §1. Метрические пространства. Пространство Rn Раньше изучались функции одной переменной f (x), которые были определены на D Í Rn. Рассмотрим некоторые свойства множеств, на которых задаются функции нескольких переменных. Множество { x, y }, состоящее из двух элементов, называется парой. Пара, как и любое множество, определяется своими элементами. Упорядоченная пара (x, y) определяется еще и порядком следования элементов, т.е. Декартовым (прямым) произведением множеств
Если A1=A2=R, то R ´ R = R2 называется числовой плоскостью. Каждой упорядоченной паре чисел (x, y) соответствует на плоскости, где введена декартова система координат, точка М (x, y), и наоборот, каждой точке на плоскости соответствует пара (x, y). Поэтому точка на плоскости отождествляется с упорядоченной парой. Прямое произведение R ´ R ´ R = R3 называется числовым трехмерным пространством. R ´ R ´....´ R = Rn - n-мерное пространство (nÎN,n > 2).
 называется точкой пространства Rn, число называется точкой пространства Rn, число  - i-й координатой этой точки. - i-й координатой этой точки.
Обозначается В пространстве Rn определяется сложение элементов, умножение элемента на действительное число. Пусть 1) 2) Пусть Е – непустое множество. Определение. Метрикой (расстоянием) на множестве Е называется неотрицательная функция r = r (х, у)³0, определенная " х, у Î Е и удовлетворяющая следующим условиям (аксиомам метрики): 1. r (х, у)=0 Û х = у (аксиома тождества); 2. r (х, у)= r (у, х) (аксиома симметрии); 3. r (х, y)£ r (х, z)+ r (z, y) " z Î Е (аксиома треугольника). Определение. Множество Е с введенной на нем метрикой r называется метрическим пространством и обозначается (Е, r). Т. о., метрическим пространством называется пара, состоящая из множества Е и метрики r на Е. Элементы метрического пространства Е называются его точками. В пространстве Rn метрика определяется следующим образом:
где
 - метрическое пространство, n -мерное евклидово пространство (можно задать другую метрику - метрическое пространство, n -мерное евклидово пространство (можно задать другую метрику  и получить и получить  - другое метрическое пространство). - другое метрическое пространство).
 ; в случае n =2, т.е. в R ´ R = R2, ; в случае n =2, т.е. в R ´ R = R2,  . .
Покажем, что расстояние в 1) 2) r (х, у)= r (у, х), т.к. 3) Пусть
 имеют место неравенства: имеют место неравенства:
Доказательство (3).
Извлекая из обеих частей квадратный корень, получим (3).
Доказательство (4).
Извлекая корень из обеих частей, получим (4). Полагая в неравенстве Минковского a = x-z, b = z-y, получим (2), т.е. аксиома 3 для r (х, у) выполнена.
Пусть
 в пространстве Rn называется множество всех точек в пространстве Rn называется множество всех точек  , удовлетворяющих неравенству , удовлетворяющих неравенству  : :  . .
Фиксированная точка a называется центром шара, число
 . .
 - открытый круг с центром в точке а (а 1, а 2), радиусом e. - открытый круг с центром в точке а (а 1, а 2), радиусом e.
При n =3,
 . .
Определение 3. Окрестностью точки Обозначается
 . .
Определение 4. Точка a называется внутренней точкой множества Е, если существует окрестность точки а, целиком лежащая во множестве Е: Совокупность всех внутренних точек множества Е называется внутренностью множества Е. Обозначается int E. Например,
 называется внешней точкой множества Е, если называется внешней точкой множества Е, если  , не содержащая ни одной точки множества Е. , не содержащая ни одной точки множества Е.
Определение 6. Точка Граничная точка может как принадлежать, так и не принадлежать множеству.
 называется предельной точкой множества Е, если в любой окрестности точки а содержится хотя бы одна точка множества Е, отличная от а. называется предельной точкой множества Е, если в любой окрестности точки а содержится хотя бы одна точка множества Е, отличная от а.
Определение 8. Точка У изолированной точки а множества Е Пример. Внутренние точки (1;3), внешние точки граничные точки {1;3;7}, предельные точки [1;3], изолированная точка {7}. Теорема 1. Точка а - предельная точка множества Е тогда и только тогда, когда в любой окрестности точки а содержится бесконечно много точек множества Е. Определение 9. Множество Е называется открытым, если все его точки являются внутренними. Определение 10. Множество Е называется замкнутым, если оно содержит все свои предельные точки. Примеры. 1) (а; b), 2) [ a; b ], 3)
Определение 11. Множество Теорема 2. Если множество Е открыто, то СЕ – замкнуто, если множество Е замкнуто, то СЕ – открыто. Определение 12. Множество Е называется ограниченным, если существует замкнутый шар, содержащий в себе множество Е: Теорема 3. Множество Е ограничено
 и и  называется множество называется множество  , где функции , где функции  непрерывны на [ a; b ], непрерывны на [ a; b ],  . .
Определение 14. Множество Е называется связным (линейно связным), если любые две его точки можно соединить непрерывной кривой, целиком лежащей в этом множестве. Определение 15. Множество
|

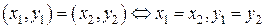 . Аналогично определяется упорядоченная тройка, четверка и т.д. Упорядоченный набор из n элементов обозначается
. Аналогично определяется упорядоченная тройка, четверка и т.д. Упорядоченный набор из n элементов обозначается  .
.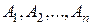 называется множество, содержащее все упорядоченные наборы
называется множество, содержащее все упорядоченные наборы  , где
, где  , т.е.
, т.е. .
. , М
, М 
 ;
;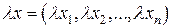 .
. , (1)
, (1)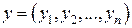 .
. , определяемое формулой (1), удовлетворяет всем аксиомам метрики.
, определяемое формулой (1), удовлетворяет всем аксиомам метрики. Û
Û  .
. .
.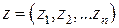 . Покажем, что
. Покажем, что . (2)
. (2) - неравенство Коши-Буняковского (3)
- неравенство Коши-Буняковского (3) - неравенство Минковского (4)
- неравенство Минковского (4) Рассмотрим квадратный трехчлен относительно
Рассмотрим квадратный трехчлен относительно  :
:

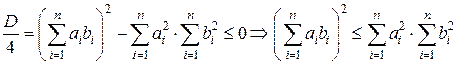 .
.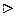

 .
. .
. .
. - проколотая окрестность точки а.
- проколотая окрестность точки а. .
. .
. называется изолированной точкой множества Е, если она не является предельной точкой множества Е.
называется изолированной точкой множества Е, если она не является предельной точкой множества Е. .
. ,
, - открытые множества,
- открытые множества, - замкнутые множества,
- замкнутые множества, называется дополнением множества Е.
называется дополнением множества Е. .
.
 .
. называется областью, если оно открыто и связно.
называется областью, если оно открыто и связно.


