Похибки обчислень
Джерела похибок. На деяких етапах розв’язування задачі на ЕОМ можуть виникати похибки, які спотворюють результати обчислень. Оцінка ступеня достовірності отриманих результатів є найважливішим питанням при організації обчислювальних робіт. Це особливо важливо за відсутності дослідних або інших даних для порівняння, які могли б в деякій мірі показати надійність чисельного методу, що використовується, і достовірність отриманих результатів. Розглянемо джерела похибок на окремих етапах розв’язування задачі. Математична модель, прийнята для опису даного процесу або явища, може внести істотні похибки, якщо в ній не враховані які-небудь важливі риси даної задачі. Зокрема, математична модель може чудово працювати в одних умовах і бути абсолютно неприйнятною в інших; тому важливо правильно враховувати область її застосування. Початкові дані задачі часто є основним джерелом похибок. Це так звані неусувні похибки, оскільки вони не можуть бути зменшені обчислювачем ні до початку розв’язування задачі, ні в процесі її розв’язування. Проведений раніше аналіз оцінки похибок при виконанні арифметичних операцій показує, що слід прагнути того, щоб всі початкові дані були приблизно однаковій точності. Істотне уточнення одних початкових даних за наявності великих похибок в інших, як правило, не приводить до підвищення точності результатів. Чисельний метод також є джерелом похибок. Це зв'язано, наприклад, із заміною інтеграла сумою, усіканням рядів при обчисленнях значень функцій, інтерполяцією табличних даних і т.п. Як правило, похибка чисельного методу регульована, тобто вона може бути зменшена до будь-якого розумного значення шляхом зміни деякого параметра (наприклад, кроку інтеграції, числа членів усіченого ряду і т. п.). Похибку методу звичайно прагнуть довести до величини, у декілька разів меншої похибки початкових даних. Подальше зниження похибки не приведе до підвищення точності результатів, а лише збільшить вартість розрахунків через необґрунтоване збільшення об'єму обчислень. Докладніше похибки методів розглядатимемо при аналізі конкретних чисельних методів. При обчисленнях за допомогою ЕОМ неминучі похибки округлень, пов'язані з обмеженістю розрядної сітки машини. Звичайно після виконання операції проводиться не округлення результату, а просте відкидання зайвих розрядів з метою економії машинного часу. Правда, в сучасних машинах передбачена свобода вибору програмістом способу округлення; відповідні засоби має в своєму розпорядженні більшість алгоритмічних мов. Максимальна відносна похибка при округленні є В сучасних машинах з пам'яттю, що виміряється в байтах, прийнята шіснадцяткова система числення, і будь-яке число з плаваючою комою містить шість значущих цифр. Отже, в цьому випадку a = 16, k = 6 і максимальна відносна похибка округлення Не дивлячись на те, що при рішенні великих задач виконуються мільярди операцій, це зовсім не означає механічного множення похибки при одному округленні на число операцій, оскільки при окремих діях похибки можуть компенсувати одна одну (наприклад, при складанні чисел різних знаків). Разом з тим, іноді похибки округлень в поєднанні з погано організованим алгоритмом можуть сильно спотворити результати. Переклад чисел з однієї системи числення в іншу також може бути джерелом похибки через те, що основа однієї системи числення не є ступенем основи іншої (наприклад, 10 і 2), Це може привести до того, що в новій системі числення число стає ірраціональним. Наприклад, число 0,1 при перекладі в двійкову систему числення приймає вигляд 0,1 = 0,00011001100... Може виявитися, що якщо з кроком 0,1 потрібно при обчисленнях пройти відрізок [0; 1] від х = 1 до х = 0, то десять кроків не дадуть точного значення х = 0. Зменшення похибок. При розгляді похибок результатів арифметичних операцій наголошувалося, що віднімання близьких чисел приводить до збільшення відносної похибки; тому в алгоритмах слід уникати подібних ситуацій. Розглянемо також деякі інші випадки, коли можна уникнути втрати точності правильною організацією обчислень. Нехай потрібно знайти суму п'яти чотирьох-розрядних чисел: S = 0.2764 + 0.3944 + 1.475 + 26.46 + 1364. Складаючи всі ці числа, а потім, округлюючи отриманий результат до чотирьох значущих цифр, одержуємо S = 1393. Проте, при обчисленні на машині, округлення відбувається після кожного складання. Припускаючи умовно сітку чотирьох-розрядною, прослідимо обчислення на машині суми чисел від найменшого до найбільшого, тобто в порядку їх запису: 0.2764 + 0.3944 = 0.6708; 0.6708 + 1.475 = 2.156; 2.156 + 26.46 = 28.62; 28.62 + 1364 = 1393. Отримали S1 = 1393, тобто вірний результат. Змінимо тепер порядок обчислень і почнемо складати числа послідовно від останнього до першого: 1364 + 26.46 = 1390, 1390 + 1.475 = 1391, 1391 + 0.3944 = 1391, 1391 + 0.2764 = 1391. Тут остаточний результат S1 = 1391, він менш точний. Аналіз процесу обчислень показує, що втрата точності тут відбувається через те, що добавляння до великого числа малих чисел не відбувається, оскільки вони виходять за рамки розрядної сітки (а + b = а при а» b). Цих малих чисел може бути дуже багато, але на результат вони все одно не вплинуть, оскільки додаються поодинці. Тут необхідно дотримуватися правила, відповідно до якого додавання чисел потрібно проводити у міру їх зростання. В машинній арифметиці через похибку округлення істотним є порядок виконання операцій, і відомі з алгебри закони комутативності (і дистрибутивності) тут не завжди виконуються. При розв’язуванні задачі на ЕОМ потрібно використовувати подібного роду «маленькі хитрощі» для поліпшення алгоритму і зниження похибок результатів. Наприклад, при обчисленні на ЕОМ значення (а + х)2 величина х може виявитися такою, що результатом складання а + х вийде а (при х «а); в цьому випадку може допомогти заміна Розглянемо ще один важливий приклад — використовування рядів для обчислення значень функцій. Запишемо, наприклад, розкладання функції sin(х) по ступенях аргументу:
За ознакою Лейбніца залишок збіжного знакозмінного ряду, тобто похибка суми скінченого числа членів, не перевищує значення першого з відкинутих членів (по абсолютній величині). Обчислимо значення функції sin (х) при х = 0.5236 (30°). Члени ряду, менші sin(0.5236)» 0.5236 - 0.2393 • Це відмінний результат в рамках прийнятої точності. Знаючи з курсу вищої математики, що це розкладання синуса справедливо при будь-якому значенні аргументу (-¥ < х < ¥), використовуємо його для обчислення функції при х =6.807 (390°). Опускаючи обчислення, одержуємо sin(6.807)» 0.5493. Відносна похибка складає тут близько 10% (замість очікуваного значення 0.01% за ознакою Лейбніца). Це пояснюється похибками округлень і способом підсумовування ряду (зліва направо, без урахування величини членів). В програмах, що використовують степеневі ряди для обчислення значень функцій, можуть бути вжиті різні заходи по запобіганню подібної втрати точності. Так, для тригонометричних функцій можна використовувати формули приведення, завдяки чому аргумент знаходитиметься на відрізку [0, 1]. При обчисленні експоненти аргумент х можна розбити на суму цілої і дробової частин Таким чином, при організації обчислень можна своєчасно розпізнати подібне «підводне каміння», коли можлива втрата точності, і спробувати потім виправити положення.
|

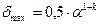 , де a — основа системи числення, k— кількість розрядів мантиси числа. При простому відкиданні зайвих розрядів ця похибка збільшується удвічі.
, де a — основа системи числення, k— кількість розрядів мантиси числа. При простому відкиданні зайвих розрядів ця похибка збільшується удвічі. .
. .
.
 , не враховуватимемо. Обчислення проведемо з чотирма вірними знаками. Отримаємо:
, не враховуватимемо. Обчислення проведемо з чотирма вірними знаками. Отримаємо: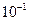 + 0.3281 •
+ 0.3281 •  = 0.500.
= 0.500.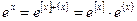 і використати розкладання в ряд тільки для
і використати розкладання в ряд тільки для 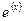 , а
, а 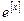 обчислювати множенням.
обчислювати множенням.


