Схемная интерпретация метода Ньютона-Рафсона при решении нелинейного уравнения
При простейшей цепи с одним нелинейным двухполюсником (см. рис.4.4) можно составить следующую систему уравнений (математическую модель схемы – ММС) в базисе узловых потенциалов:
Рисунок 4.4-Электрическая цепь с нелинейным резистором
Применим к уравнению итерационную формулу Ньютона, получим:
или
Это можно интерпретировать таким образом: мы линеаризуем нелинейный двухполюсник (рис. 4.5,а), используя разложение в ряд Тейлора:
где
что соответствует схеме замещения, приведенной на рис.4.5, б).
а) б) Рисунок 4.5 – Нелинейный двухполюсник а) и схемная интерпретация линеаризации нелинейного двухполюсника б)
Рисунок 4.6 – Электрическая цепь со схемой замещения нелинейного резистора Для преобразованной схемы на рис 4.6 узловое уравнение
или
что соответствует методу Ньютона для заданной схемы. Рассмотрим применение метода Ньютона для более сложной схемы, показанной на рис. 4.7.
а) б) Рисунок 4.7-Электрическая цепь с диодом а) и его итерационная схема замещения б) Модель вольтамперной характеристики диода
где
Итерационная модель диода
Для схемы на рис 4.7,б) имеем:
Рисунок 4.8 – Геометрическая иллюстрация применения метода Ньютона для схемы, приведенной на рис. 4.7
|
,
.
.
,
,
,
,
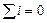- ток насыщения,
- тепловой потенциал.
.
,
,
,
