Рівняння хорди АВ:
 .
.
Звідси, поклавши  та
та  , отримаємо:
, отримаємо:
 . (1)
. (1)
Далі, застосовуючи цей прийом до відрізка  , отримаємо друге наближення кореня:
, отримаємо друге наближення кореня:
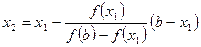 .
.
Продовжуючи процес далі, отримаємо формулу методу хорд:
 (2)
(2)
Умова 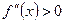 забезпечувала нам розташування точного значення кореня
забезпечувала нам розташування точного значення кореня 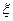 всередині відрізка
всередині відрізка 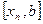 на кожному етапі процесу обчислення (на кожній ітерації). Це випливає з аналізу мал. 1.
на кожному етапі процесу обчислення (на кожній ітерації). Це випливає з аналізу мал. 1.
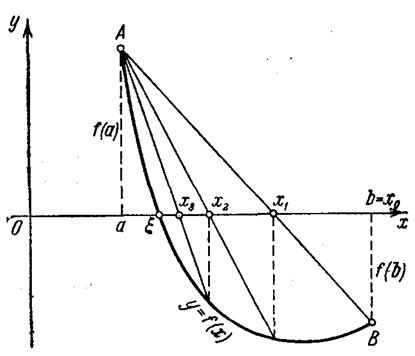
Мал. 2
Якщо  і
і 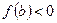 (мал. 2), то потрібно користуватися такою формулою методу хорд (при цьому, як і раніше, вважаємо, що
(мал. 2), то потрібно користуватися такою формулою методу хорд (при цьому, як і раніше, вважаємо, що 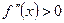 ):
):
 (3)
(3)
Якщо 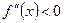 , то можна розглядувати рівняння
, то можна розглядувати рівняння  .
.
Узагальнюємо отримані результати:
1) нерухомим є той кінець відрізка  , для якого знак функції
, для якого знак функції  співпадає зі знаком її другої похідної
співпадає зі знаком її другої похідної  , тобто
, тобто  ; за
; за 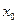 приймаємо інший (протилежний до нерухомого) кінець відрізка;
приймаємо інший (протилежний до нерухомого) кінець відрізка;
2) послідовні наближення  лежать по той бік від кореня
лежать по той бік від кореня 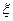 , де функція
, де функція  має знак, протилежний знаку її другої похідної
має знак, протилежний знаку її другої похідної  . У обох випадках кожне наступне наближення
. У обох випадках кожне наступне наближення  ближче до кореня
ближче до кореня 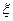 , ніж попереднє
, ніж попереднє  .
.
Для оцінки точності наближення можна скористатися формулою (5) §1:
 ,
,
де  при
при 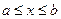 ;
;
а також формулою:
 .
.
Приклад. Знайти додатний корінь рівняння
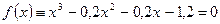
з точністю до 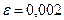 .
.
Розв’язок. Перш за все відділимо корінь. Так як
 ,
, 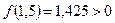 , то
, то  .
.
Перша похідна:
 .
.
Друга похідна
 при
при  .
.
Отже: нерухомий кінець  ,
,  .
.
Послідовно застосовуючи формулу (2), матимемо:

| 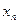
| 
| 
| 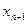
|
|
|
| -0,6
| 
| 
|
|
| 1,15
| -0,173
| 
| 
|
|
| 1,190
| -0,036
| 
| 
|
|
| 1,198
| -0,0072
| 
|
|
|
|
|
|
|
|
Так як при  маємо
маємо
 ,
,
то можна оцінити похибку точніше:
 .
.
Зауважимо, що точний корінь рівняння є  .
.

 .
. та
та  , отримаємо:
, отримаємо: . (1)
. (1) , отримаємо друге наближення кореня:
, отримаємо друге наближення кореня: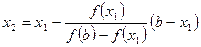 .
. (2)
(2)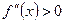 забезпечувала нам розташування точного значення кореня
забезпечувала нам розташування точного значення кореня 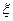 всередині відрізка
всередині відрізка 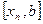 на кожному етапі процесу обчислення (на кожній ітерації). Це випливає з аналізу мал. 1.
на кожному етапі процесу обчислення (на кожній ітерації). Це випливає з аналізу мал. 1.
 і
і 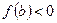 (мал. 2), то потрібно користуватися такою формулою методу хорд (при цьому, як і раніше, вважаємо, що
(мал. 2), то потрібно користуватися такою формулою методу хорд (при цьому, як і раніше, вважаємо, що 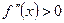 ):
): (3)
(3)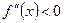 , то можна розглядувати рівняння
, то можна розглядувати рівняння  .
. , для якого знак функції
, для якого знак функції  співпадає зі знаком її другої похідної
співпадає зі знаком її другої похідної  , тобто
, тобто  ; за
; за 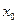 приймаємо інший (протилежний до нерухомого) кінець відрізка;
приймаємо інший (протилежний до нерухомого) кінець відрізка; лежать по той бік від кореня
лежать по той бік від кореня  . У обох випадках кожне наступне наближення
. У обох випадках кожне наступне наближення  ближче до кореня
ближче до кореня  ,
, при
при 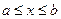 ;
; .
.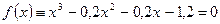
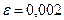 .
. ,
, 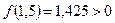 , то
, то  .
. .
. при
при  .
. ,
,  .
.
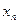

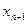







 маємо
маємо ,
, .
. .
.


