Процес відділення коренів починається з встановлення знаків функції  у граничних точках
у граничних точках  и
и  області її існування.
області її існування.
Потім встановлюються знаки функції  у ряді проміжних точок
у ряді проміжних точок  , вибір яких враховує особливості функції
, вибір яких враховує особливості функції  . Якщо виявиться, що для деякого
. Якщо виявиться, що для деякого  матиме місце нерівність
матиме місце нерівність  , то в силу теореми 1 на інтервалі
, то в силу теореми 1 на інтервалі  матимемо корінь рівняння
матимемо корінь рівняння  . Потім потрібно впевнитися, чи є цей корінь єдиний. Для відділення коренів практично часто буває достатньо здійснити процес половинного поділу, наближено ділячи даний інтервал
. Потім потрібно впевнитися, чи є цей корінь єдиний. Для відділення коренів практично часто буває достатньо здійснити процес половинного поділу, наближено ділячи даний інтервал  на дві, чотири, вісім і т. д. рівних частин (до деякого кроку) та визначаючи знаки функції
на дві, чотири, вісім і т. д. рівних частин (до деякого кроку) та визначаючи знаки функції  в точках поділу. Корисно пам’ятати, що алгебраїчне рівняння
в точках поділу. Корисно пам’ятати, що алгебраїчне рівняння  -го степеня
-го степеня
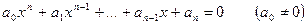
має не більше  дійсних коренів. Тому, якщо для такого рівняння ми отримали
дійсних коренів. Тому, якщо для такого рівняння ми отримали  змін знаків, то всі корені його відділені.
змін знаків, то всі корені його відділені.
Приклад 1. Відділити корені рівняння
 . (2)
. (2)
Рішення. Складаємо приблизну схему:
- 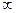
| -
|
| -3
| -
|
| -1
| +
|
|
| +
|
|
| -
|
|
| +
|
+ 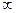
| +
|
Отже, рівняння (2) має три дійсні корені, що лежать в інтервалах  .
.
Якщо існує неперервна похідна  і корені рівняння
і корені рівняння  легко обчислюються, то процес відділення коренів рівняння (1) можна упорядкувати. Для цього, очевидно, достатньо підрахувати лише знаки функції
легко обчислюються, то процес відділення коренів рівняння (1) можна упорядкувати. Для цього, очевидно, достатньо підрахувати лише знаки функції  в точках нулів її похідної і в граничних точках
в точках нулів її похідної і в граничних точках  і
і  .
.
Приклад 2. Відділити корені рівняння
 . (3)
. (3)
Розв’язок. Тут  , тому
, тому  при
при 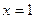 .
.
Маємо
 .
.
Отже, рівняння (3) має тільки два дійсні корені, з яких один лежить в інтервалі  , а інший — в інтервалі
, а інший — в інтервалі  .
.
Приклад 3. Визначити число дійсних коренів рівняння
 . (4)
. (4)
Розв’язок. Оскільки  і
і  ,
,  те рівняння (4) має тільки один дійсний корінь.
те рівняння (4) має тільки один дійсний корінь.
Дамо тепер оцінку похибки наближеного кореня.
Теорема 2 (без доведення). Нехай 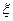 — точний, а
— точний, а  — наближений корені рівняння
— наближений корені рівняння  , що знаходяться на одному і тому ж відрізку
, що знаходяться на одному і тому ж відрізку  , причому
, причому  при
при  .
.
У такому разі справедлива оцінка
 . (5)
. (5)
Зауваження. Формула (5) може дати грубі результати, і її не завжди зручно застосовувати. Тому на практиці тим або іншим способом звужують загальний інтервал  , що містить корінь
, що містить корінь 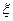 і його наближене значення
і його наближене значення  , і вважають
, і вважають  .
.
Приклад 4. Наближеним коренем рівняння  є
є  . Оцінити абсолютну похибку цього кореня.
. Оцінити абсолютну похибку цього кореня.
Розв’язок. Маємо  .
.
Оскільки при  одержуємо
одержуємо
 ,
,
то точний корінь 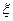 міститься в інтервалі
міститься в інтервалі  . Похідна
. Похідна  монотонно зростає. Тому її якнайменшим значенням в даному інтервалі є:
монотонно зростає. Тому її якнайменшим значенням в даному інтервалі є:
 .
.
Звідси по формулі (5) отримаємо:
 .
.
§2. Метод половинного поділу (метод дихотомії)
Нехай дано рівняння
 , (1)
, (1)
де функція  неперервна на
неперервна на 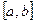 і
і  .
.
Для пошуку кореня рівняння (1), що належить відрізку 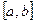 ділимо цей відрізок навпіл (на дві рівні частини). Якщо
ділимо цей відрізок навпіл (на дві рівні частини). Якщо  , то
, то  є коренем рівняння. Якщо
є коренем рівняння. Якщо  , то вибираємо ту з половин
, то вибираємо ту з половин  чи
чи  , на кінцях якої функція
, на кінцях якої функція  має протилежні знаки. Новий звужений відрізок
має протилежні знаки. Новий звужений відрізок  знову ділимо навпіл і вибираємо ту з половин
знову ділимо навпіл і вибираємо ту з половин  чи
чи  , на кінцях якої функція
, на кінцях якої функція  має протилежні знаки, і так далі. У результаті отримаємо на деякому етапі точний корінь рівняння (1), або ж нескінчену послідовність вкладених один в одного відрізків
має протилежні знаки, і так далі. У результаті отримаємо на деякому етапі точний корінь рівняння (1), або ж нескінчену послідовність вкладених один в одного відрізків  таких, що
таких, що
 (2)
(2)
і
 (3).
(3).
Для кожного фіксованого  можна стверджувати, що корінь рівняння (1) знаходиться на відрізку
можна стверджувати, що корінь рівняння (1) знаходиться на відрізку  . Наближеним значенням кореня можна вважати середину цього відрізка:
. Наближеним значенням кореня можна вважати середину цього відрізка:
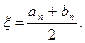
Похибка у цьому випадку:
 .
.
Приймаючи значення  досить великим (виконуючи досить велике число половинних поділів відрізка), можна досягнути високої точності обчислень.
досить великим (виконуючи досить велике число половинних поділів відрізка), можна досягнути високої точності обчислень.
Якщо корені рівняння (1) не відділені на відрізку 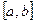 , то таким способом можна знайти хоча б один з коренів рівняння (1), але немає гарантії, що ми знайдемо всі корені.
, то таким способом можна знайти хоча б один з коренів рівняння (1), але немає гарантії, що ми знайдемо всі корені.
Метод дихотомії практично зручно застосовувати для грубого знаходження кореня даного рівняння, оскільки при збільшенні точності значно зростає об'єм обчислювальної роботи.
Зауважимо, що метод половинного поділу легко реалізується на комп'ютерах. Програма обчислення складається так, щоб машина знаходила значення лівої частини рівняння (1) в середині кожного з відрізків  і вибирала відповідну половину його.
і вибирала відповідну половину його.
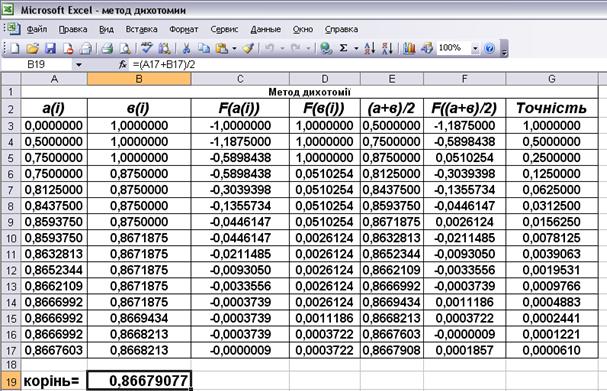
Приклад. Методом половинного поділу уточнити корінь рівняння  , що лежить на відрізку
, що лежить на відрізку  .
.
Розв’язок. Послідовно маємо:

| 
| 
| 
| 
| 
| 
|
|
|
|
| -1
|
| 
| 0,5
|
|
| 0,5
|
| -1,19
|
| 
| 0,25
|
|
| 0,75
|
| -0,59
|
| 
| 0,125
|
|
| 0,75
| 0,875
| -0,59
| 0,05
| 
| 0,0625
|
|
| 0,8125
| 0,875
| -0,304
| 0,05
| 
| 0,03125
|
Приймаємо:
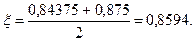
Виконаємо це завдання у програмі Excel.
§ 3. Метод хорд (спосіб пропорційних частин)
Розглянемо (в передумовах § 2) більш швидкий спосіб знаходження кореня 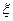 рівняння
рівняння  , що лежить на заданому відрізку
, що лежить на заданому відрізку 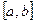 , такому, що
, такому, що  .
.
Нехай для визначеності  і
і  . Покладемо також, що
. Покладемо також, що 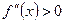 . Тоді, замість того, щоб ділити відрізок
. Тоді, замість того, щоб ділити відрізок 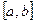 навпіл, більш логічно розділити його у відношенні
навпіл, більш логічно розділити його у відношенні  .
.
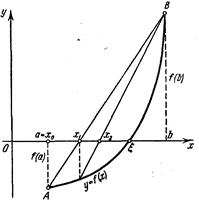
Геометрично метод хорд еквівалентний заміні кривої  хордою, що проходить через точки
хордою, що проходить через точки  та
та  (мал. 1).
(мал. 1).

 у граничних точках
у граничних точках  и
и  області її існування.
області її існування. , вибір яких враховує особливості функції
, вибір яких враховує особливості функції  матиме місце нерівність
матиме місце нерівність  , то в силу теореми 1 на інтервалі
, то в силу теореми 1 на інтервалі  матимемо корінь рівняння
матимемо корінь рівняння  . Потім потрібно впевнитися, чи є цей корінь єдиний. Для відділення коренів практично часто буває достатньо здійснити процес половинного поділу, наближено ділячи даний інтервал
. Потім потрібно впевнитися, чи є цей корінь єдиний. Для відділення коренів практично часто буває достатньо здійснити процес половинного поділу, наближено ділячи даний інтервал  на дві, чотири, вісім і т. д. рівних частин (до деякого кроку) та визначаючи знаки функції
на дві, чотири, вісім і т. д. рівних частин (до деякого кроку) та визначаючи знаки функції  -го степеня
-го степеня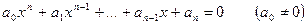
 . (2)
. (2)
 .
. і корені рівняння
і корені рівняння  легко обчислюються, то процес відділення коренів рівняння (1) можна упорядкувати. Для цього, очевидно, достатньо підрахувати лише знаки функції
легко обчислюються, то процес відділення коренів рівняння (1) можна упорядкувати. Для цього, очевидно, достатньо підрахувати лише знаки функції  . (3)
. (3) , тому
, тому 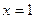 .
. .
. , а інший — в інтервалі
, а інший — в інтервалі  .
. . (4)
. (4) і
і  ,
,  те рівняння (4) має тільки один дійсний корінь.
те рівняння (4) має тільки один дійсний корінь.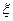 — точний, а
— точний, а  — наближений корені рівняння
— наближений корені рівняння  , причому
, причому  при
при  .
. . (5)
. (5) , що містить корінь
, що містить корінь  .
. є
є  . Оцінити абсолютну похибку цього кореня.
. Оцінити абсолютну похибку цього кореня. .
. одержуємо
одержуємо ,
, . Похідна
. Похідна  монотонно зростає. Тому її якнайменшим значенням в даному інтервалі є:
монотонно зростає. Тому її якнайменшим значенням в даному інтервалі є: .
. .
.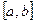 і
і  .
. , то
, то  є коренем рівняння. Якщо
є коренем рівняння. Якщо  , то вибираємо ту з половин
, то вибираємо ту з половин  чи
чи  , на кінцях якої функція
, на кінцях якої функція  знову ділимо навпіл і вибираємо ту з половин
знову ділимо навпіл і вибираємо ту з половин  чи
чи  , на кінцях якої функція
, на кінцях якої функція  таких, що
таких, що (2)
(2) (3).
(3). можна стверджувати, що корінь рівняння (1) знаходиться на відрізку
можна стверджувати, що корінь рівняння (1) знаходиться на відрізку  . Наближеним значенням кореня можна вважати середину цього відрізка:
. Наближеним значенням кореня можна вважати середину цього відрізка: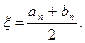
 .
. і вибирала відповідну половину його.
і вибирала відповідну половину його. , що лежить на відрізку
, що лежить на відрізку  .
.











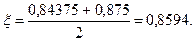

 .
. і
і  . Покладемо також, що
. Покладемо також, що 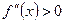 . Тоді, замість того, щоб ділити відрізок
. Тоді, замість того, щоб ділити відрізок  .
. хордою, що проходить через точки
хордою, що проходить через точки  та
та  (мал. 1).
(мал. 1).



