Впорядкування СЛАР
Вибір головного елемента для підвищення точності. Метод вибору головного елемента дозволяє підвищити точність розв’язування СЛАР. Якщо припустити в СЛАР, що Якщо найважливішою вимогою до розрахунку є точність, то доцільно як ведучий вибрати елемент з максимальною абсолютною величиною. Якщо вибрати такий елемент серед коефіцієнтів рівнянь при даній змінній (в нашому прикладі при змінній Так, в прикладі:
при частковому впорядкуванні міняємо місцями 1-е і 3-е рівняння. Отримаємо
При повному впорядкуванні додатково до цього поміняємо місцями 1-й і 3-й стовпець, отримаємо:
Відзначимо, що частковий вибір провідного елемента не змінює порядок проходження змінних, як це відбувається у разі повного впорядкування. 3.7 Ітераційні методи Ітерація – результат повторного використання якої-небудь математичної операції. Розв’язки, знайдені за допомогою прямих методів, звичайно містять похибки, викликані округленням. У ряді випадків ці похибки можуть бути значними і необхідно знайти спосіб їх зменшення. Розглянемо один із способів, що дозволяє уточнити розв’язок, отриманий за допомогою прямого методу. Знайдемо розв’язок СЛАР за допомогою прямого методу.
Нехай це буде вектор
Підставляючи цей розв’язок у ліві частини рівняння цієї системи, отримаємо деяке значення
У матричному вигляді АХ(0) = В(0). Введемо позначення:
Віднімаючи кожне рівняння системи (3.18) від відповідного рівняння системи (3.17), з урахуванням вказаних позначень, отримаємо:
Розв’язуючи цю систему, знаходимо значення похибок
Таким же способом можна знайти нові поправки до розв’язку
Процес продовжується до тих пір, поки всі чергові поправки Розглянутий процес уточнення розв’язку представляє фактично ітераційний метод розв’язування системи лінійних рівнянь. При цьому для знаходження чергового наближення, тобто на кожній ітерації, розв'язується система рівнянь вигляду (3.19) з однією і тією ж початковою матрицею Розв’язування систем рівнянь за допомогою розглянутого методу, а також при використанні інших ітераційних методів, зводиться до наступного: вводяться початкові дані (коефіцієнти рівнянь, допустимі похибки
то ітераційний процес припиняється. Зауважимо. що в цій схемі не передбачений випадок відсутності збіжності. Для запобігання непродуктивних витрат машинного часу, в алгоритм потрібно вводити допустиме число ітерацій, досягши якого, обчислення припиняються.
3.8. Метод простої ітерації Найпростішим ітераційним методом рішення СЛАР є ітераційний метод Гауса (метод простої ітерації). Проілюструємо цей метод на прикладі розв’язування СЛАР 3-го порядку
Припустимо, що Маємо:
Задамо деякі початкові (нульові) наближення
Використовуючи обчислені значення
Кожні наступні наближення знаходимо аналогічно:
У загальному випадку для СЛАР
Ітераційний процес продовжується до тих пір, поки на сусідніх ітераціях значення
або
|

 , то в цьому випадку не можна використовувати метод Гаусса, оскільки в за алгоритмом методу потрібно ділити перше рівняння системи на
, то в цьому випадку не можна використовувати метод Гаусса, оскільки в за алгоритмом методу потрібно ділити перше рівняння системи на 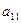 . Елемент, на який виконується ділення, називають ведучим (головним). У такій ситуації слід поміняти перше рівняння на інше, в якому
. Елемент, на який виконується ділення, називають ведучим (головним). У такій ситуації слід поміняти перше рівняння на інше, в якому  , і процес стає реалізовуваним.
, і процес стає реалізовуваним. ), то матимемо справу з частковим вибором провідного елемента (частковим впорядкуванням). Якщо вибрати максимальний елемент зі всієї матриці, то такий вибір називається повним (повне впорядкування).
), то матимемо справу з частковим вибором провідного елемента (частковим впорядкуванням). Якщо вибрати максимальний елемент зі всієї матриці, то такий вибір називається повним (повне впорядкування).

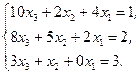
 (3.17)
(3.17) .
. , відмінне від
, відмінне від 
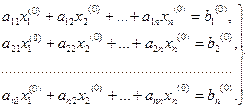 (3.18)
(3.18)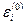 – похибки значень невідомих,
– похибки значень невідомих,  – нев'язки, тобто
– нев'язки, тобто ,
, 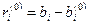 ,
,  .
. (3.19)
(3.19) :
:
 і наступні наближення розв’язку:
і наступні наближення розв’язку: ;
;
 не стануть достатньо малими.
не стануть достатньо малими. , але з різними правими частинами.
, але з різними правими частинами. , початкове наближення невідомих
, початкове наближення невідомих  ), потім організовується циклічний обчислювальний процес, кожний цикл якого представляє одну ітерацію; в результаті кожного такого циклу виходять нові значення невідомих. Якщо на черговому кроці для кожного
), потім організовується циклічний обчислювальний процес, кожний цикл якого представляє одну ітерацію; в результаті кожного такого циклу виходять нові значення невідомих. Якщо на черговому кроці для кожного  буде виконана умова
буде виконана умова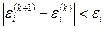 (3.20)
(3.20) (3.21)
(3.21)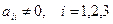 . Розв’яжемо перше рівняння відносно
. Розв’яжемо перше рівняння відносно  , друге рівняння – відносно
, друге рівняння – відносно  , третє – відносно
, третє – відносно  .
.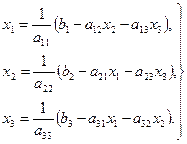 (3.22)
(3.22) :
: (3.23)
(3.23)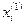 , знайдемо наступні (другі) наближення
, знайдемо наступні (другі) наближення  :
:

 го порядку:
го порядку: . (3.24)
. (3.24) та
та  не відрізнятимуться один від одного на задану величину похибки, тобто
не відрізнятимуться один від одного на задану величину похибки, тобто (3.25)
(3.25) , якщо
, якщо  . (3.26)
. (3.26)


