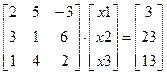ОБРОБКА ТАБЛИЧНИХ ДАНИХ
В цьому розділі розглянемо тільки основні напрями обробки даних: інтерполяцію і апроксимацію, які є базою для вирішення інших задач обробки табличних даних, наприклад, задач згладжування, чисельних методів інтеграції і т.д.
2.1 Інтерполяція
Основна задача інтерполяції – знаходження значень таблично заданої функції в тих точках всередині даного інтервалу, де вона не задана. Приклад. Залежність якості зору підлітка від тривалості щодобового перебування за комп’ютером (дані отримані шляхом опитування) задана у таблиці:
Приклад задачі інтерполяції – встановити, якою буде якість зору, якщо підліток щодобово сидітиме за комп’ютером 2 години, 1,5 годин, 3 години тощо?
Екстраполяція – це знаходження значень такої функції в точках за межами заданого інтервалу. Приклад задачі екстраполяції – встановити, якою буде якість зору, якщо підліток щодобово сидітиме за комп’ютером 4,3 години, 4,5 години, 0,5 години тощо? В обох випадках початкові табличні дані можуть бути отримані експериментально (тоді проміжні дані принципово відсутні), або розрахунковим шляхом по складній залежності (проміжні дані отримати складно або дорого, але можливо). 2.2 Концепція інтерполяції
Рішення задач інтерполяції і екстраполяції забезпечується побудовою інтерполяційної функції Якщо інтерполяційна функція Для вирішення задачі інтерполяції необхідно розглянути три проблеми: · вибір інтерполяційної функції · оцінка похибки інтерполяції · розміщення вузлів інтерполяції для забезпечення найбільшої можливої точності відновлення початкової функції Вибір інтерполяційної функції в загальному випадку є досить складною і важливою задачею, особливо якщо пам'ятати, що через задані точки можна провести будь-яку кількість функцій (рис.2.1).
Малюнок 2.1 - Ілюстрація інтерполяції.
Проте найбільше застосування як інтерполяційна функція отримав поліном вигляду
Всі інтерполяційні функції у вигляді поліномів дають одні і ті ж результати, але з різними витратами. Це пояснюється тим, що поліном n-ого степеня, що містить Коефіцієнти Що стосується вибору вузлів інтерполяції, то вони, як правило, розміщуються рівномірно на відрізку інтерполяції, хоча в деяких випадках для підвищення точності вибираються спеціальним чином. Спочатку розглянемо деякі види шматкової інтерполяції, а саме: лінійну, квадратичну і сплайн-інтерполяцію.
2.3 Лінійна і квадратична інтерполяції
Найпростішим видом локальної інтерполяції є лінійна інтерполяція. Вона полягає в тому, що задані точки Для і-го інтервалу можна написати рівняння прямої, що проходить через точки
Звідси
Для визначення наближеного значення Для випадку квадратичної інтерполяції як інтерполяційний многочлен на відрізку Тут невідомими є
Інтерполяція для будь-якої точки х з інтервалу
Приклад: Знайти наближене значення функції
а) При лінійній інтерполяції х=0.32 знаходиться між вузлами0.3 і 0.4. В цьому випадку
При
б) При квадратичній інтерполяції складемо систему рівняньдля найближчих до точки х=0.32 вузлів:
відповідно
Маємо систему рівнянь:
Розв’язуючи цю систему, знаходимо:
Тоді шукане значення
2.5 Глобальна інтерполяція. Многочлен Лагранжа. Нехай відомі значення функції
де
Якщо розкрити добутки всіх дужок в чисельнику (в знаменнику всі дужки є числами), то отримаємо поліном n-го порядку від х, тобто в чисельнику n співмножників першого порядку. Наступний поліном Лагранжа не що інше, як звичайний поліном n-го порядку, але записаний в іншій формі. Підставляючи l(x) у вираз для L(x), отримаємо
Неважко помітити, що у вузлах інтерполяції:
Оцінити похибку інтерполяції в точці
де Отже, щоб оцінити погрішність, треба знати Зформули (2.15) можна отримати вираз для лінійної
2.6 Глобальна інтерполяція. Многочлен Ньютона У загальному випадку інтерполяція по формулах Ньютона може здійснюватися для довільно розташованих вузлів інтерполяції, але частіше – для рівномірно розташованих вузлів. Тоді Метод використовує поняття скінчених різниць:
Для визначення різниці k – го порядку потрібне знання всіх точок від
Можна помітити, що за наявності n+1 точок (0,1,2,.., n), скінчену різницю 1- го порядку можна обчислити тільки для перших n точок (0,1,2,....,n –1), скінчену різницю n – го порядку – тільки для нульової точки, а k– го порядку - тільки для перших n - k+1 точок, тобто треба знати k точок попереду. Інтерполяційниймногочлен Ньютона записується таким чином:
Це теж поліном n – гопорядку, якщо виконати відповідні множення, то скінчені різниці у виразі – це числові коефіцієнти, обчисленіпо заданих точках. Часто замість х вводять безрозмірну величину q, що показує, скільки міститься кроків від
Тоді
Обидві приведені формули називаються першим інтерполяційним многочленом Ньютона для інтерполяції вперед.
В цьому випадку
Похибку інтерполяції, як і для многочлена Лагранжа, можна оцінити так:
Використовування скінчених різниць, що є своєрідними аналогами похідних безперервних функцій, допомагає знаходити похибку інтерполяції, використовуючи співвідношення:
Тоді для отримання наближеного значення
Аналогічно можна знайти похибку і в методі Лагранжа при рівномірному кроці.
Приклад. Задана таблиця Отже, n+1=3, n=2
Скористаємося першою інтерполяційною формулою Ньютона:
Оцінимо похибку знайденого значення у. З таблиці знаходимо, що М3=0,001, тоді
Формули Лагранжа, Ньютона і інші породжують один і той же многочлен. Різниця лише в алгоритмі їх побудови. Вибір способу інтерполяції визначається різними міркуваннями: точністю, часом обчислень, похибками округлення тощо. Підвищення точності інтерполяції доцільно проводити за рахунок зменшення кроку і спеціального розташування вузлових точок
2.7 Апроксимація У процесі обробки емпіричних даних необхідно враховувати помилки цих даних. Ці помилки умовно можна розділити на 3 групи за їх походженням і величиною: систематичні, випадкові, грубі. Систематичні помилки звичайно дають відхилення в одну сторону від істинного значення. Вони можуть бути постійними або закономірно змінюватися від експерименту до експерименту, їх причини і характер відомі. Ці помилки викликаються умовами експерименту (температура, вологість тощо), дефектом вимірювального приладу і т.д. Ці помилки можна врахувати і виправити. Випадкові помилки визначаються великим числом чинників і не можуть бути усуненими і врахованими. Вони мають випадковий характер і не повторюються від експерименту до експерименту. Багатократне повторення експерименту дозволить оцінити величину цієї випадкової помилки. Грубі помилки явно спотворюють результат вимірювання, вони надмірно великі і, як правило, зникають при повторенні досвіду. Враховуючи вищевикладене, немає сенсу будувати інтерполяційний многочлен, що проходить точно через отримані точки. Достатньо побудувати наближену (апроксимуючу) функцію Побудова апроксимуючої залежності за експериментальними даними складається з 2-х етапів: - підбір загального виду апроксимуючої залежності; - визначення найкращих значень параметрів цієї залежності. Якщо характер залежності невідомий, то експериментальні точки наносять на графік і приблизно вибирають залежність з геометричних міркувань шляхом порівняння її з відомими функціями (лінійної, показової, логарифмічної, степеневої тощо). Успіх визначається досвідом і інтуїцією дослідника. Після визначення формули у вигляді
необхідно знайти такі параметри Міра наближення для різних видів апроксимацій може бути різною. Так, при рівномірному наближенні за міру наближення використовують різницю (відхилення)
При цьому вимагається, щоб
В цьому випадку говорять, що функція Проте у ряді випадків не потрібна така досить жорстка вимога до відхилень, особливо при обробці експериментальних даних. Тим більше, побудова апроксимуючої функції, яка задовольняє умовам рівномірного наближення, пов’язана зі значними технічними труднощами. Цілком прийнятне так зване середньоквадратичне наближення, яке згладжує деякі неточності функції
а) б) Малюнок 2.2-рівномірне а), і середньоквадратичне б) наближення Мірою відхилення в цьому випадку є величина S, рівна сумі квадратіврізниць між значеннями функцій
При цьому необхідно підібрати коефіцієнт
2.8. Побудова апроксимуючої залежності Існує декілька методів розв’язування задачі побудови апроксимуючої залежності. Найпростіший з них – метод вибраних точок. Він складається з наступних етапів: - отримані експериментальні точки наносять на координатну площину; - проводиться найпростіша плавна лінія, що максимально близько примикає до експериментальних точок; - вибираються на цій лінії точки і записуються їх координати (число точок дорівнює числу коефіцієнтів вибраної апроксимуючої функції); - складається для цих точок система рівнянь і визначаються з неї коефіцієнти функції.
Метод середніх. Він полягає в тому, що параметри
Отримане рівняння використовується для визначення коефіцієнтів Наприклад
Розв’язуючи цю систему рівнянь, знаходимо невідомі коефіцієнти.
Метод найменших квадратів (МНК). Запишемо суму квадратів відхилень (2.26) для всіх точок
Параметри (коефіцієнти )
Розв’язуючи цю систему Приклад 1. У ролі апроксимуючої функції
Тоді Звідки, після узяття частинних похідних, отримуємо систему лінійних рівнянь
Групуючи коефіцієнт при невідомих
Цю систему можна записати компактніше:
Приклад 2. Вивести емпіричну формулу для наведеної нижче табличної залежності f(х), використовуючи метод найменших квадратів МНК.
Побудуємо емпіричний точковий графік.
Візуальний аналіз побудови дозволяє обрати на роль апроксимуючої функції квадратичну параболу
Тобто m=2, n=4. Система рівнянь для визначення коефіцієнтів
Для розрахунку коефіцієнтів системи лінійних рівнянь складемо допоміжну таблицю.
Коефіцієнти обчислюються по формулах
Отримуємо наступну систему рівнянь:
З якої знаходимо
Маємо апроксимуючу функцію:
Зауваження: 1. З формул обчислення коефіцієнтів видно, що всі коефіцієнти 2. Розв’язки системи нормальних рівнянь
3. РОЗВ’ЯЗУВАННЯ СИСТЕМ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ (СЛАР)
Системи лінійних алгебраїчних рівнянь в обчисленнях мають дуже велике значення, оскільки до них зводиться наближене розв’язування широкого круга обчислювальних задач, у тому числі систем нелінійних алгебраїчних рівнянь і диференціальних рівнянь. Теорія розв’язування лінійних систем достатньо добре розроблена, є велике число різноманітних програмних засобів для розв’язування самих різних систем рівнянь: обумовлених, блочних, стрічкових, з розрідженими матрицями тощо. Тому тут детально не розглядатимемо всі методи, а згадаємо лише основні ідеї і їх особливості.
3.1 Концепція методів Методи розв’язування СЛАР звичайно розділені на дві великі групи: точні (або прямі) і наближені ітераційні. Точні (прямі) методи дозволяють для будь-яких систем у принципі знайти точні значення невідомих після скінченого числа арифметичних операцій, кожна з яких виконується точно. Наближені ітераційні методи одержують розв’язок в результаті, у принципі, нескінченного процесу наближень. З прямих методів найбільш поширені методи Гауса, Крамера і LU-перетворення, набагато рідше використовується метод оберненої матриці. Метод Крамера (з використанням визначників) вимагає дуже великих обчислень вже при розв’язуванні системи 5 рівнянь, тому використовується тільки в учбовій літературі. З ітераційних методів використовуються в основному методи простої ітерації і метод Гаусса-Зейделя. 3.2 Метод Гаусса (метод послідовного виключення змінних) Чисельне розв’язування систем лінійних рівнянь часто базується на методі Гаусса. Він ґрунтується на тому факті, що складання одного рівняння системи з іншим, помноженим на константу, не змінює розв’язку системи. Нагадаємо, що матрична форма СЛАР
має вид:
Тут
Запишемо рівняння
Розділимо перше рівняння на
Помножимо це рівняння на
Такий вибір множника забезпечує рівність нулю коефіцієнта
забезпечує рівність нулю всіх коефіцієнтів в першому стовпці матриці А, за виключенням
Верхній індекс у дужках вказує на те, що коефіцієнти були один раз змінені. Ця операція еквівалентна виключенню з усіх рівнянь системи (крім першого) змінної На наступному кроці виключимо з розгляду перше рівняння і застосуємо аналогічну процедуру до рівнянь від другого до n-го. Запишемо формули для обчислення нових значень коефіцієнтів, за винятком тих, які стають рівними 0 при j=2, і
i=3, 4..., n; j= 3, 4..., n+1. Повторимо процедуру для всіх рядків матриці А. Якщо вважати елементи початкової матриці А як такі, що отримані на нульовому кроці перетворень, тобто
k=1, 2..., n; i=k+1..., n; j=k+1..., n+1. В результаті система рівнянь приводиться до трикутного вигляду:
..
Це повністю відповідає послідовному виключенню змінних з системи рівнянь (прямий хід методу Гаусса). Для визначення невідомих необхідно провести зворотну підстановку (зворотний хід методу Гаусса). В загальному вигляді зворотну підстановку можна записати так:
Тут верхні індекси опущені. Прямий хід методу Гаусса вимагає виконання ~ Зворотна підстановка (зворотний хід методу Гаусса) вимагає ~ Приклад розв’язування СЛАР методом Гаусса Розв’яжемо систему лінійних алгебраїчних рівнянь третього порядку:
Необов'язково переписувати кожного разу всю систему рівнянь; достатньо прослідити зміну її чисельних коефіцієнтів, які ми зведемо для зручності в розширену матрицю коефіцієнтів. Початкова матриця I крок: k=1; j=2, 3, 4; i=2, 3, 4 при к=0
II крок: k=2; j=3, 4; i=3, 4 III крок: k=3; j=4; i =4
Таким чином, у результаті здійснення прямого ходу методу Гаусса, ми отримали систему з верхньою трикутною матрицею.
Розв’язуємо цю систему зворотним ходом: х3=3; х2=-37/13 + 21/13 . х3=2; х1=3/2- 5/2 х2+3/2. х3= 1.
|

 , яка приблизно замінює початкову таблично задану функцію
, яка приблизно замінює початкову таблично задану функцію  , і проходить через задані точки – вузли інтерполяції, тобто
, і проходить через задані точки – вузли інтерполяції, тобто  . За допомогою цієї функції
. За допомогою цієї функції  у будь-якій точці.
у будь-якій точці. ;
;
 (2.1)
(2.1) параметр (коефіцієнт), і проходить через усі задані
параметр (коефіцієнт), і проходить через усі задані  полінома n-ого степеня визначаються шляхом розв’язування системи рівнянь
полінома n-ого степеня визначаються шляхом розв’язування системи рівнянь  з'єднуютьсяпрямолінійними відрізками, а функція
з'єднуютьсяпрямолінійними відрізками, а функція  апроксимується ламаною з вершинами в даних точках.
апроксимується ламаною з вершинами в даних точках. та
та  у вигляді:
у вигляді: .
.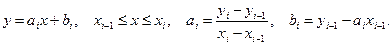 (2.2)
(2.2) приймається квадратний многочлен
приймається квадратний многочлен  .
. вони знаходяться з умови проходження многочлена через три точки
вони знаходяться з умови проходження многочлена через три точки 
 . (2.3)
. (2.3) проводитьсяпо трьох найближчихдо неї вузлах.
проводитьсяпо трьох найближчихдо неї вузлах.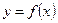 при х=0,32, якщо відома таблиця її значень:
при х=0,32, якщо відома таблиця її значень: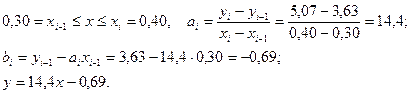
 маємо:
маємо: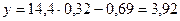 .
.



 в точці х=0.32 буде:
в точці х=0.32 буде: .
. точках
точках  . Для інтерполяції функції в довільній точці х, що належить відрізку
. Для інтерполяції функції в довільній точці х, що належить відрізку  , необхіднопобудуватиінтерполяційний поліном n-го порядку, який в методі Лагранжа має вигляд:
, необхіднопобудуватиінтерполяційний поліном n-го порядку, який в методі Лагранжа має вигляд: (2.14)
(2.14)
 (2.15)
(2.15)
 (друга проблема інтерполяції) можна по формулі:
(друга проблема інтерполяції) можна по формулі: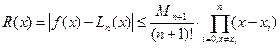 (2.16)
(2.16) - максимальне значення
- максимальне значення  -ої похідної початкової функції f(x) на відрізку
-ої похідної початкової функції f(x) на відрізку  , що не завжди можливо.
, що не завжди можливо. і квадратичної
і квадратичної  інтерполяції без обчислення відповіднихкоефіцієнтів.
інтерполяції без обчислення відповіднихкоефіцієнтів. , де
, де  .
. - різниці 1-го порядку
- різниці 1-го порядку - різниці 2-го порядку
- різниці 2-го порядку - різниці 3-го порядку
- різниці 3-го порядку до
до  :
: (2.17)
(2.17) (2.18)
(2.18) до заданої точки
до заданої точки 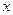 .Ця величина визначається таким чином:
.Ця величина визначається таким чином: .
.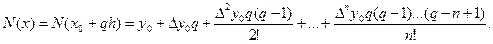 (2.19)
(2.19) Для інтерполяції в правому кінці відрізка
Для інтерполяції в правому кінці відрізка  , коли для k останніх точок не можна обчислити потрібні скінчені різниці, використовують многочленНьютона, в якому скінчені різниці обчислюються справа наліво, тобто здійснюється інтерполяція назад. Такий многочлен називається другим інтерполяційниммногочленомНьютона для інтерполяції назад.
, коли для k останніх точок не можна обчислити потрібні скінчені різниці, використовують многочленНьютона, в якому скінчені різниці обчислюються справа наліво, тобто здійснюється інтерполяція назад. Такий многочлен називається другим інтерполяційниммногочленомНьютона для інтерполяції назад.
 (2.20)
(2.20) . (2.21)
. (2.21) ,
,  ,
,  ,…,
,…,  .
. достатньо мати декілька (або навіть одну) додаткових точок
достатньо мати декілька (або навіть одну) додаткових точок  , з використанням яких легко знайти максимальне значення скінченої різниці (n+1) – го порядку:
, з використанням яких легко знайти максимальне значення скінченої різниці (n+1) – го порядку: 
 (2.22)
(2.22)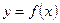 , необхідно знайти у(2.05). Використовуємо для інтерполяції тільки три перші точки, а решту – для оцінок похибки.
, необхідно знайти у(2.05). Використовуємо для інтерполяції тільки три перші точки, а решту – для оцінок похибки.


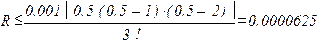
 . Підвищення степеня інтерполяційного многочлена також підвищує точність, проте не завжди (залежить від поведінки похідної
. Підвищення степеня інтерполяційного многочлена також підвищує точність, проте не завжди (залежить від поведінки похідної 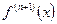 . Тому на практиці прагнуть використовувати многочлени малого степеня (лінійний, квадратичний).
. Тому на практиці прагнуть використовувати многочлени малого степеня (лінійний, квадратичний). , яка в цілому найбільш близько проходить біля даних точок початкової функції
, яка в цілому найбільш близько проходить біля даних точок початкової функції  (2.23)
(2.23) , при яких формула дала б добре наближення до виміряних даних, не обов'язково проходячи через ці точки.
, при яких формула дала б добре наближення до виміряних даних, не обов'язково проходячи через ці точки.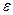 між значеннями апроксимуючої функції
між значеннями апроксимуючої функції 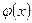 і початкової
і початкової  у всіх точках деякого відрізка
у всіх точках деякого відрізка  :
: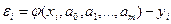
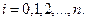 (2.24)
(2.24) . (2.25)
. (2.25)
 (2.26)
(2.26)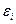 .
. залежності (2.23) визначаються з умови рівності нулю суми відхилень (2.24) у всіх точках
залежності (2.23) визначаються з умови рівності нулю суми відхилень (2.24) у всіх точках 
 коефіцієнтів, то ця сума розбивається на
коефіцієнтів, то ця сума розбивається на 
 :
:
 як функції багатьох змінних
як функції багатьох змінних 
 .
.
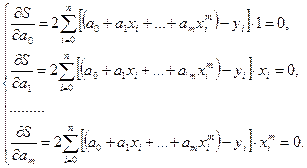
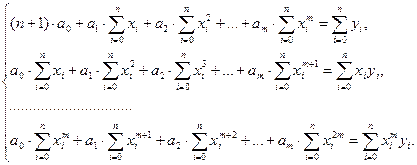


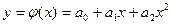 .
. :
:
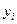





 ,
,  ,
,  ,
, ,
,  ,
,  ,
,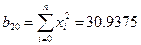 ,
,  ,
,  ,
, ,
,  ,
,  .
.

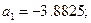



 однакові при к+l=const.
однакові при к+l=const. цієї системи, тому вони (розв’язки) можуть істотно змінюватися при навіть незначних змінах цих коефіцієнтів. Тому бажано не округлювати розраховані коефіцієнти
цієї системи, тому вони (розв’язки) можуть істотно змінюватися при навіть незначних змінах цих коефіцієнтів. Тому бажано не округлювати розраховані коефіцієнти  порядку
порядку
 .
. - матриця системи рівнянь,
- матриця системи рівнянь, - вектор-стовпчик правих частин рівнянь системи.
- вектор-стовпчик правих частин рівнянь системи.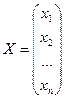 - вектор-стовпчик невідомих розв’язків системи.
- вектор-стовпчик невідомих розв’язків системи. через
через 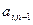 , тоді:
, тоді: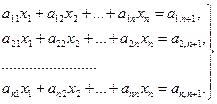 (3.1)
(3.1)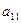 , і запишемо його:
, і запишемо його: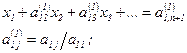
 де
де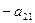 , і складемо його з другим рівнянням. Коефіцієнти отриманого другого рівняння
, і складемо його з другим рівнянням. Коефіцієнти отриманого другого рівняння
 .
.
 . Аналогічно для інших рівнянь підстановка
. Аналогічно для інших рівнянь підстановка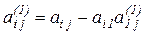 i=2, 3..., n j= 2..., n+1
i=2, 3..., n j= 2..., n+1 . В результаті отримаємо
. В результаті отримаємо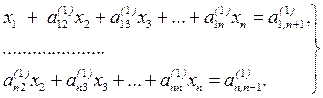
 .
. тобто для j=3,4.,n+1.
тобто для j=3,4.,n+1.
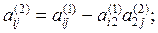
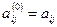 , то загальну формулу методу виключення Гаусса можна представити таким чином:
, то загальну формулу методу виключення Гаусса можна представити таким чином: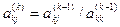
 ;
;


 (3.3)
(3.3) .
. i=n-1, n-2..., 1. (3.4)
i=n-1, n-2..., 1. (3.4) , де під операцією розуміється комбінація множення і віднімання, а n – порядок матриці.
, де під операцією розуміється комбінація множення і віднімання, а n – порядок матриці. операцій.
операцій.