Простейшие методы

 

К простейшим методам можно отнести методы прямоуголь­ников (левых и правых) и трапеций. В первом случае подынте­гральная функция заменяется горизонтальной прямой (у = с₀) со значением ординаты (т.е. значением функции) соответственно слева или справа участка, во втором случае — наклонной прямой (у=с₁х+с₀).

Формулы интегрирования при разбиении отрезка [ a,b ] на n частей с равномерным шагом h соответственно приоб­ретают вид:

 

• для одного участка интегрирования:

 

- метод прямоугольников

,

,

;

 

- метод трапеций

,

,

 

• для n участков интегрирования:

 

- метод прямоугольников

,

,

;

 

- метод трапеций

.

Нетрудно заметить, что в методе прямоугольников интеграл вычислится абсолютно точно только при f(x) = с (const), а в мето­де трапеций — при f(x) линейной или кусочно-линейной.

 

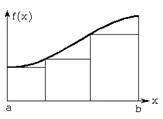
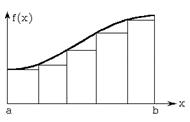
а) б)

а) — с 3 участками разбиения отрезка интегрирования [a, b];

б) — с 5 участками разбиения отрезка интегрирования [a, b]

Рисунок 5.1 – Иллюстрация метода левых прямоугольников

 

На рис. 5.1 для сравнения приведены примеры прямоугольни­ков при различном числе участков. Наглядно видно, что площадь всех прямоугольников на правом рисунке меньше отличается от площади под кривой f(x), чем на левом.

Метод прямоугольников не находит практического применения в силу значительных погрешностей, что тоже видно из рис. 5.1.

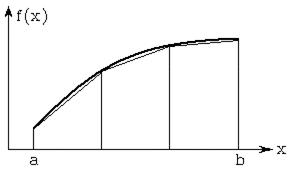
Рисунок 5.2 – Иллюстрация метода трапеций

 

На рис. 5.2 приведен пример вычисления интеграла методом трапеций. По сравнению с методом прямоугольников, метод трапеций более точный, так как трапеция точнее заменяет соответствующую криволинейную трапецию, чем прямоугольник.

Погрешность ε; вычисления интеграла методом трапеций при использовании двойного просчета на практике может быть опре­делена из следующего соотношения:

,

где I_n и I_n/2 — соответственно значения интеграла при числе раз­биений п и n/2.

Существуют и аналитические выражения для определения погрешности, но они требуют знания второй произ­водной подынтегральной функции, поэтому имеют только теоре­тическое значение. С использованием двойного просчета можно организовать автоматический подбор шага интегрирования (т.е. числа разбиений n) для обеспечения заданной погрешности ин­тегрирования (последовательно удваивая шаг и контролируя по­грешность).

Пример. Вычислить

1) для всего интервала;

2) с делением интервала на четыре участка.

Аналитическое вычисление данного интеграла дает

I =arctg(l) – arctg(0) =0,7853981634.

В нашем слу­чае:

1) Dх=l, x₀=0; x₁=l;

2) Dх =0,25 (1/4), x₀=0, x₁=0,25, x₂=0,5, x₃ =0,75, x₄=1,

.

Вычислим интеграл методом левых прямоугольников:

1) ;

2)

Методом правых прямоугольников:

1) ;

2)

Вычислим методом трапеций:

1) ;

2)
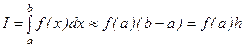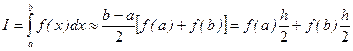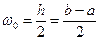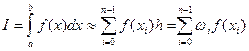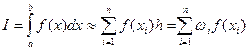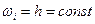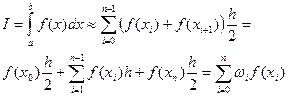
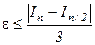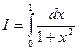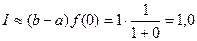
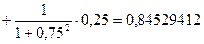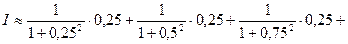